Графические изображения выборки. Полигон и гистограмма

Для наглядного представления о выборке часто используют различные графические изображения выборки. Простейшими изображениями выборки являются полигон и гистограмма. Пусть выборка задана вариационным рядом: (х₁ ; n₁ ); (х₂ ; n₂ ); ( х₃ ; n₃ ); … (х_k ; n_k ) _. Полигоном частот называют ломаную с вершинами в указанных точках.

Полигоном относительных частот называют ломаную с вершинами в точках

(х₁ ; 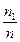); (х₂ ; 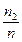); ( х₃ ; ); … (х_k ; )

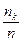Ясно, что полигон относительных частот получается из полигона частот сжатием вдоль оси ординат в n раз, где n — объем выборки.

При большом объеме выборки более наглядное представление о ней дает гистограмма. Чтобы построить гистограмму частот, промежуток от наименьшего значения выборки до наибольшего ее значения разбивают на несколько частичных промежутков длины h. Для каждого частичного промежутка вычисляют сумму s_i частот значений выборки, попавших в этот промежуток. Значение x_i выборки, совпавшее с правым концом промежутка, относят к следующему промежутку (если x_i — не наибольшее значение выборки). Затем на каждом частичном промежутке, как на основании, строят прямоугольник с высотой . Объединение всех построенных таким образом прямоугольников называют гистограммой частот. Итак, гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные промежутки длины h, а высотами — отрезки длины , где s_i — сумма частот значений выборки, попавших

в i-й промежуток.

Из определения гистограммы ясно, что ее площадь равна объему выборки.

При решении задач в зависимости от объема выборки в большинстве случаев целесообразно брать 10-20 частичных промежутков.

Аналогично определяют и строят гистограмму относительных частот.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные промежутки длины h, а высотами — отрезки длины 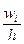, где w_i - суммы относительных частот значении выборки, попавших в i-й промежуток. Площадь гистограммы относительных частот, очевидно, равна единице.

Пусть имеется некоторая выборка объема n: x_1, х₂, x_{3, …} x_n . Выброчной средней называется среднее арифметическое значений выборки:

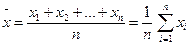(5)

Если выборка задана статистическим рядом (3) или выборочным распределением (4), то формулу (5) естественно записать в следующем виде:

(6)

Выборочной дисперсией называетсясреднее арифметическое квадратов отклонений значений выборки от выборочной средней.

(7)

Если выборка задана статистическим рядом (3) или выборочным распределением (4), то формулу (7) можно записать так:

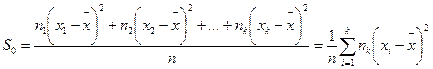(8)

Формулы (7) и (8) можно преобразовать к более удобному для вычислений виду:

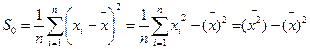(9)

т. е. выборочная дисперсия равна среднему квадратов значений выборки без квадрата выборочной средней.

Исправленной выборочной дисперсией называется

(10)

где S₀ — выборочная дисперсия, п — объем выборки. Отсюда, используя формулу (7),

(11)

Примеры по выполнению практической работы

Пример 1. Составить для выборки 1, 10, -2, 1,0, 1, 10, 7, -2, 10, 10, 7

вариационный ряд и найти ее размах.

Решение: записав заданную выборку в виде неубывающей последовательности, получим вариационный ряд

-2,-2,0, 1, 1, 1,7,7, 10, 10, 10, 10.

Размах данной выборки равен 10 - (-2) =12.

Пример 2Для выборки 3,8,-1,3, 0, 5,3,-1,3, 5 определить объем и размах. Записать выборку в виде вариационного ряда и в виде статистического ряда. Найти выборочное распределение. Построить полигон частот.

Решение: Объем выборки n = 10, ее размах равен 8 - (-1) = 9. Записав значения выборки в виде неубывающей последовательности получим вариационный ряд

-1,-1,0, 3,3, 3,3, 5, 5, 8.

Статистический ряд можно записать в виде последовательности пар чисел - (-1;2), (0;1), (3;4), 5;2), (8;1) или в виде таблицы

-1

Для контроля находим сумму частот: 2+ 1 +4 + 2+ 1 = 10 и убеждаемся в том, что она равна объему выборки.

Вычислив относительные частоты, найдем выборочное распределение:

-1

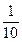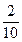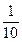Для контроля убеждаемся в том, что сумма относительных частот равна единице:

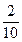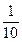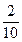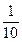+ + + + =1.

Полигон частот для заданной выборки имеет вид:

Пример 3. При измерении напряжения в электросети получена следующая выборка:

218, 221, 215, 225, 225, 217,

224, 220, 220, 219, 221, 219,

222, 227, 218, 220, 223, 230,

223, 216, 224, 227, 220, 222

(данные выражены в вольтах). Построить гистограмму частот, если число частичных промежутков равно 5.

Решение: наименьшее значение выборки равно 215, наибольшее — 230.

Находим длину частичных промежутков . Подсчитываем с учетом кратности число значений выборки, попавших в каждый промежуток.

Для первого промежутка [215; 218) это число равно 3, для второго [218; 221) оно равно 8, для третьего [221; 224) — 6, для четвертого [224; 227) — 5, для пятого [227; 230] — 2. Следовательно, высоты прямоугольников (слева направо), образующих гистограмму, равны По полученным данным строим гистограмму

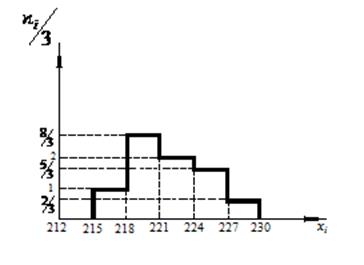
Для контроля убеждаемся в том, что площадь гистограммы равна объему выборки:

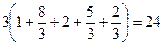
Пример 4. На основании данных о средней заработной плате работников в области в тыс. руб., которые помещены в интервальный вариационный ряд в таблицу, построить гистограмму распределения частот зарплаты работников:

Заработная плата	1-3	3-5	5-7	7-9	9-11	11-13
Число Работников

Решение: при построении гистог­раммы по оси абсцисс откладываются значения изучаемого признака (границы интервалов), а по оси у – соответствую­щие частоты, в том случае, если интервалы одинаковой величины. Используя мастер диаграмм в MS Excel, получим гистограмму:

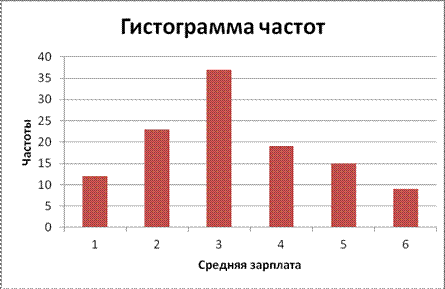
Гистограмма распределения частот зарплаты работников

Пример 3. Для выборки 4,5,3,2, 1,2,0,7,7,3 найти выборочную среднюю 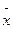, выборочную дисперсию S₀, исправленную выборочную дисперсию S.

Решение: объем выборки п = 10. По формуле (5) находим выборочную среднюю:

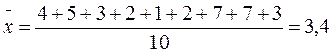
Чтобы найти выборочную дисперсию, воспользуемся формулой (9). Для этого вычислим среднее квадратов значений выборки:

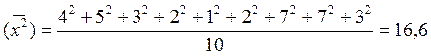
Теперь по формуле (9) находим S₀ = 16,6 -3,4²= 5,04. Наконец, используя формулу (10), вычисляем исправленную выборочную дисперсию:

Пример 4. Для выборки 3,8-1,3,0,5,3,4,3,5 найти выборочную среднюю 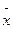, выборочную дисперсию S₀, исправленную выборочную дисперсию S.

Решение: статистический ряд для для данной выборки имеет вид

-1

Объем выборки п=10. Выборочную среднюю найдем по формуле (6):

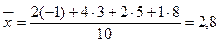
Вычислим среднее квадратов значений выборки:

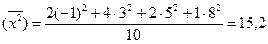
Согласно формуле (9) находим выборочную дисперсию:

S₀ = 15,2-2,8²= 7,36.

Для вычисления исправленной выборочной дисперсии воспользуемся формулой (10):

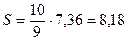
Задания для практического занятия:

Вариант 1

1.Для выборки 1,1,2,-5,4,3,3,8,8,1 определите объем и размах. Запишите выборку в виде вариационного ряда и в виде статистического ряда. Найдите выборочное распределение.

2. Для выборки, заданной статистическим рядом

постройте 1) полигон частот; 2) полигон относительных частот;

3. Для выборки, заданной вариационным рядом -5, -5, 2, 3, 5,10,15, 15, 20, 20, найдите выборочную среднюю 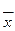; выборочную дисперсию S₀, несмещенную выборочную дисперсию S.

4. Произведено выборочное обследование коммерческих фирм по затратам на ре

кламу, результаты которого представлены в таблице:

Затраты на рекламу (усл. ден. ед.)	Кол-во фирм
40-60
60-80
80-100
100-120
120-140

По данным выборочного обследования постройте гистограмму частот, используя мастер диаграмм в MS Excel.

Вариант 2

1.Для выборки -3,1,2,4,3,4,4,1,2,1 определите объем и размах. Запишите выборку в виде вариационного ряда и в виде статистического ряда. Найдите выборочное распределение.

2. Для выборки, заданной статистическим рядом

-1

постройте 1) полигон частот; 2) полигон относительных частот

3. Для выборки, заданной статистическим рядом

-1

найдите выборочную среднюю 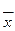; выборочную дисперсию S₀, несмещенную

выборочную дисперсию S;

4. В результате выборочного обследования коммерческих банков о размере прибыли за год получено следующее распределение:

Размер прибыли (млн руб.)	Число банков
10- 20 20-30 30-40 40-50 50-60

По данным выборочного обследования постройте гистограмму частот, используя мастер диаграмм в MS Excel.

Вариант 3

1.Для выборки 4,8,8,-4,2, 3,2,7,2,2 определите объем и размах. Запишите выборку в виде вариационного ряда и в виде статистического ряда. Найдите выборочное распределение.

2. Для выборки, заданной статистическим рядом

постройте 1) полигон частот; 2) полигон относительных частот

3. Для выборки, заданной вариационным рядом 2, 4, 4, 4, 5, 5, 5, 5, 10, 10, найдите выборочную среднюю 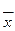; выборочную дисперсию S₀, несмещенную выборочную дисперсию S;

4. На заводе проведено выборочное обследование выра­ботки деталей рабочими в день. По результатам наблю­дений построили вариационный ряд.

Количество деталей
Количество рабочих

По данным выборочного обследования постройте гистограмму частот, используя мастер диаграмм в MS Excel.

Вариант 4

1.Для выборки 3,4,5,6,7,2,-4,-2,3,6 определите объем и размах. Запишите выборку в виде вариационного ряда и в виде статистического ряда. Найдите выборочное распределение.

2. Для выборки, заданной статистическим рядом

постройте 1) полигон частот; 2) полигон относительных частот;

3. Для выборки, заданной статистическим рядом

найдите выборочную среднюю 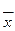; выборочную дисперсию S₀, несмещенную

выборочную дисперсию S.

4.Выборочные данные декоративных изделий показали отклонения от стандартного размера, которые помеще­ны в вариационный рад:

Отклонение	10,2	10,4	10,6	10,8		11,2	11,4	11,6	11,8
Количество изделий

По данным выборочного обследования постройте гистограмму частот, используя мастер диаграмм в MS Excel.

Контрольные вопросы

1. Что называют: а) генеральной совокупностью; б) выборочной совокупностью; в) объемом выборки?

2. Дайте определение вариационного ряда. Что называют размахом выборки?

3. Как для данной выборки получают статистический ряд и выборочное распределение?

4. Какие графические изображения выборок вы знаете?

5. Чему равна площадь гистограммы относительных частот?

6. Дайте определение выборочных характеристик: а) выборочной средней;

б) выборочной дисперсии;

7. Как связаны между собой выборочная дисперсия и исправленная выборочная дисперсия?