Алгоритм построения логических схем.

1. Определить число логических переменных.

2. Определить количество логических операций и их порядок.

3. Изобразить для каждой логической операции соответствующий ей логический элемент.

4. Соединить логические элементы в порядке выполнения логических операций.

Пример 6. По заданной логической функции 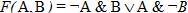построить логическую схему.

1. Число логических переменных = 2 (A и B).

2. Количество операций = 5 (2 инверсии, 2 конъюнкции, 1 дизъюнкция). Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции.

3. Схема будет содержать 2 инвертора, 2 конъюнктора и 1 дизъюнктор.

4. Построение надо начинать с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые, в свою очередь, подаются один входной сигнал нормальный и один инвертированный (с инверторов).

Логические законы и правила преобразования логических выражений

Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.

В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений.

1. Закон двойного отрицания: ;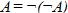

2. Переместительный (коммутативный) закон:

· для логического сложения: ;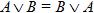

· для логического умножения: ;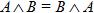

3. Сочетательный (ассоциативный) закон:

· для логического сложения: ;

· для логического умножения: ;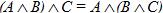

4. Распределительный (дистрибутивный) закон:

· для логического сложения: ;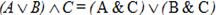

· для логического умножения: ;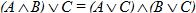

5. Законы де Моргана:

· для логического сложения: ;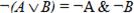

· для логического умножения: ;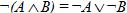

6. Закон идемпотентности:

· для логического сложения: ;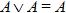

· для логического умножения: ;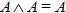

7. Законы исключения констант:

· для логического сложения: ;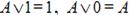

· для логического умножения: ;

8. Закон противоречия: ;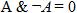

9. Закон исключения третьего: ;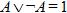

10. Закон поглощения:

· для логического сложения: ;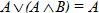

· для логического умножения: ;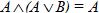

11. Правило исключения импликации: ;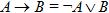

12. Правило исключения эквиваленции: .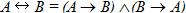

Справедливость этих законов можно доказать составив таблицу истинности выражений в правой и левой части и сравнив соответствующие значения.

Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.

Пример 7. Упростить логическое выражение .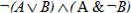

Согласно закону де Моргана: .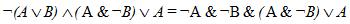

Согласно сочетательному закону: .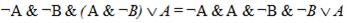

Согласно закону противоречия и закону идемпотентности: .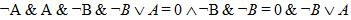

Согласно закону исключения 0: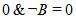

Окончательно получаем /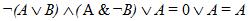

Задания для практического занятия:

Вариант 1

1. Составить таблицу истинности логического выражения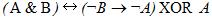

2. Построить логическую схему функции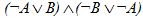

3. Упростить логическое выражение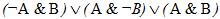

4. Определить, являются ли два высказывания эквивалентными A & (B v C) и A & B & C

5. Определить истинность или ложность высказываний ((X<5) v (X<3)) & ((X<2) v (X<1)) при X=1

Вариант 2

1. Составить таблицу истинности логического выражения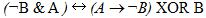

2. Построить логическую схему функции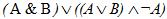

3. Упростить логическое выражение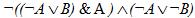

4. Определить, являются ли два высказывания эквивалентными (A & B v A & (B v C)) и B & (A v C)

5. Определить истинность или ложность высказываний ((X<5) v (X<3)) & ((X<2) v (X<1) при X=3

Вариант 3

1. Составить таблицу истинности логического выражения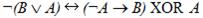

2. Построить логическую схему функции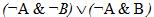

3. Упростить логическое выражение

4. Определить, являются ли два высказывания эквивалентными C v B v (A v C) и A & B v C & B

5. Определить истинность или ложность высказываний X>1 & ((X<5) v (X<3)) при X=2

Вариант 4

1. Составить таблицу истинности логического выражения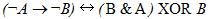

2. Построить логическую схему функции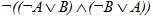

3. Упростить логическое выражение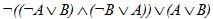

4. Определить, являются ли два высказывания эквивалентными (А v В) v B & C и A & (B ∨ C)

5. Определить истинность или ложность высказываний ((X>2) v (X<2)) v (X>4) при X=1

Вариант 5

1. Составить таблицу истинности логического выражения .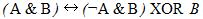

2. Построить логическую схему функции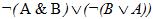

3. Упростить логическое выражение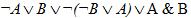

4. Определить, являются ли два высказывания эквивалентными

5. Определить истинность или ложность высказываний X>1 & ((X<5) v (X<3)) при X=2

Контрольные вопросы:

1. Что такое высказывание (приведите пример)?

2. Что такое составное высказывание (приведите пример)?

3. Укажите приоритеты выполнения логических операций.

4. Составьте таблицу истинности для следующих операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.

5. Изобразите функциональные элементы: конъюнктор, дизъюнктор, инвертор.

6. Какие логические выражения называются равносильными?

7. Запишите основные законы алгебры логики.