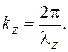Одношлейфное согласование волновода с нагрузкой

Цель работы: практическое осуществление одношлейфного согласования волновода с нагрузкой.

Для выполнения работы необходимо ознакомиться с теоретическим материалом 4.

Входная проводимость линии

Входная проводимость в сечении линии с координатой 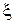определяется как отношение комплексных амплитуд тока и напряжения в этом сечении:

(6.1)

Нормированная входная проводимость 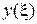определяется как

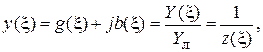(6.2)

где 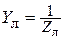– волновая проводимость линии.

Из выражений (4.4) и (6.2) вытекает, что 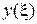жестко связана с коэффициентом отражения:

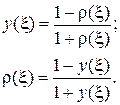(6.3)

Как следует из формул (6.1)–(6.3), закономерности поведения активных и реактивных входных проводимостей аналогичны закономерностям для активных и реактивных сопротивлений. В частности, для проводимости в сечениях линии, где формируются максимумы и минимумы напряжения, справедливы следующие выражения:

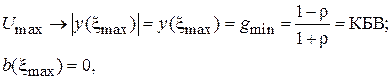(6.4)

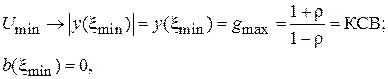(6.5)

(см. рис. 4.2).

Трансформирующее действие отрезков линий в отношении проводимостей описывается формулой пересчета, вытекающей из (4.7, а):

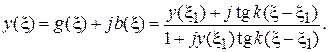
Практически пересчеты проводимостей выполняют с помощью круговых диаграмм проводимостей. Техника пересчетов проводимостей ничем не отличается от техники пересчета сопротивлений, нужно лишь считать кривые и 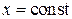кривым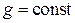и и 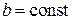. Единственное отличие появляется в привязке линии к диаграмме по КБВ и минимуму (максимуму) напряжения. На диаграмме проводимостей линией минимумов является нижняя вертикальная полуось, а линией максимумов – верхняя полуось. Это связано с тем, что в сечении линии, где формируется максимум напряжения, проводимость (чисто активная) равна КСВ. В точках минимума напряжения (нижняя полуось) проводимость линии чисто активная и равная КБВ. Поэтому слегка видоизменяется процедура обработки результатов при измерении проводимости нагрузки: точку 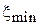на диаграмме проводимостей следует брать на нижней вертикальной полуоси.

6.2. Расчет входных сопротивлений и проводимостей в линиях
с последовательными или с параллельными неоднородностями

Если в линию передачи вводятся неоднородности, то на эквивалентных схемах они представляются более или менее сложными комбинациями сосредоточенных элементов, включенных в линию. Простейшими среди них являются последовательные или параллельные элементы (рис. 6.1, а, б). Далее рассматривается случай, когда параллельная неоднородность включается в линию на некотором расстоянии l от известной оконечной нагрузки

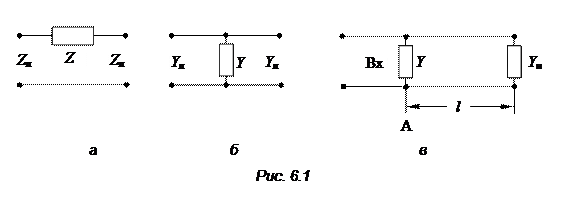(рис. 6.1, в) и необходимо рассчитать входную проводимость в сечении А.

Задача.

В схеме рис. 6.1, в: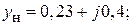

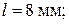
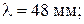
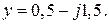
Найдите .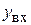

Решение. На круговой диаграмме проводимостей наносим точку Н, соответствующую 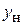(рис. 6.2). Через эту точку проходит окружность фиксированного КБВ = 0,2. Из точки Н следует совершить переход в точку А, т. е. в направлении к генератору. Отсчет по шкале перемещений для точки Н: 0,064. Добавляя к нему относительное расстояние 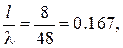получим 0,064+0,167 = 0,231 – отсчет, соответствующий точке А. Проводим через него и центр диаграммы луч; точка его пересечения с окружностью КБВ = 0,2 дает точку А. С кривых, проходящих через А. считываем величины активной и реактивной части трансформированной проводимости: 3,8 и 2,2. Складывая это число с 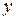, получим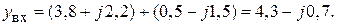

6.3. 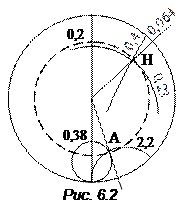Нормированные сопротивления и проводимости

Лабораторная работа проводится с использованием волноводных линий передачи. Одной из характерных особенностей волноводных волн является то, что для них невозможно ввести понятие волны «напряжения и тока», опираясь на единообразный подход, пригодный для любых волноводов и любых типов волн и них. Этим волноводные моды в корне отличаются от Т-волн, для которых существует универсальный способ введения понятий напряжения и тока (см. 2.6).

Указанная особенность не позволяет дать корректное определение понятию «волновое сопротивление волновода» как отношению напряжения волны к току волны. Несмотря на это, в теории волноводов все же широко пользуются понятиями входных сопротивлений и проводимостей, но речь идет только о нормированных (безразмерных) сопротивлениях и проводимостях. Нормированное сопротивление входит в теорию волноводов через коэффициент отражения. Допустим, в волноводе в условиях одномодового режима распространяются прямая и обратная волны, амплитуды которых относительно нормированных волн равны и 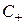. Продольные распределения электрического поля этих волн записываются как 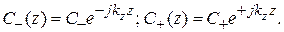Отношение этих величин и есть коэффициент отражения:

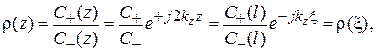
где 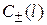– комплексные амплитуды падающей и отраженной волн на нагрузке (на конце волновода); 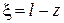– продольная координата, отсчитываемая от конца волновода (от нагрузки) в сторону генератора.

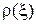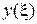Эта величина имеет совершенно четкий физический смысл и применима к любым модам. Входное нормированное сопротивление и входная нормированная проводимость волновода вводятся через с помощью формул теории длинных линий, выражающих жесткую связь и с 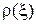(см. (4.4) и (6.3)).

Таким образом, связи (4.4) и (6.3) не вытекают из самой теории волноводов, а привносятся в нее извне – из теории длинных линий. Поэтому нормированная входная проводимость для волновода – величина вторичного характера, определяемая по аналогии с длинными линиями с помощью (6.3).

Аналогичным образом понятие нормированного сопротивления (проводимости) распространяется и на волноводные нагрузки.

Основная причина, по которой нормированные проводимости и сопротивления волноводов широко используются на практике, состоит в желании распространить на волноводы те методы расчета, которые разработаны в теории длинных линий с использованием этих понятий.

Что касается закономерностей поведения и 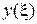в волноводах, то они в точности такие же, как и в длинных линиях, поскольку коэффициент отражения 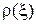в любых линиях передачи ведет себя совершенно одинаково. Полностью переносятся на волноводы методы расчета по круговым диаграммам. Следует лишь учитывать, что волновым числом здесь является продольное волновое число 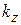рабочей моды: