Свойства входного сопротивления линии
В 2 было показано, что напряжение 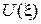 , ток
, ток 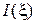 и
и 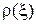 меняются вдоль линии периодически с периодом
меняются вдоль линии периодически с периодом  . Из формулы (4.4) следует, что и сопротивление
. Из формулы (4.4) следует, что и сопротивление  имеет тот же период изменения. Поэтому поведение
имеет тот же период изменения. Поэтому поведение  достаточно рассмотреть на полуволновом отрезке, заключенном, например, между соседними максимумами напряжения (рис. 4.2). В сечениях линии с координатами
достаточно рассмотреть на полуволновом отрезке, заключенном, например, между соседними максимумами напряжения (рис. 4.2). В сечениях линии с координатами  и
и  фаза коэффициента отражения
фаза коэффициента отражения 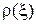 принимает значение, кратное
принимает значение, кратное  где
где 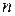 – целое число; коэффициент отражения
– целое число; коэффициент отражения 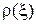 положителен,
положителен,  . Поэтому числитель дроби формулы (4.4) принимает максимальное значение
. Поэтому числитель дроби формулы (4.4) принимает максимальное значение  , а знаменатель – минимальное значение
, а знаменатель – минимальное значение  . Напряжение и ток в линии син
. Напряжение и ток в линии син 
фазны. Таким образом, в сечениях линии с координатами  ,
,  сопротивление линии имеет чисто вещественное и максимальное значение, численно совпадающее с КСВ в линии:
сопротивление линии имеет чисто вещественное и максимальное значение, численно совпадающее с КСВ в линии:
 (4.8)
(4.8)
На рис. 4.2, а, д приведены векторные диаграммы на комплексной плоскости для этих случаев ( 
 ).
).
Как следует из формулы для 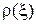 (4.5), фаза коэффициента отражения
(4.5), фаза коэффициента отражения  меняется по линейному закону от
меняется по линейному закону от 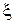 , так что вектор
, так что вектор 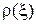 на комплексной плоскости поворачивается по часовой стрелке, а модуль его
на комплексной плоскости поворачивается по часовой стрелке, а модуль его 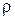 остается неизменным. Поэтому в сечении
остается неизменным. Поэтому в сечении 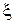 (где
(где  ) положение
) положение 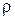 будет, как на рис. 4.2, г. Из этого рисунка видно, что модуль числителя (модуль напряжения)
будет, как на рис. 4.2, г. Из этого рисунка видно, что модуль числителя (модуль напряжения)  а модуль знаменателя
а модуль знаменателя  Поэтому сопротивление по модулю будет меньше, чем в сечении
Поэтому сопротивление по модулю будет меньше, чем в сечении  :
:  . Поскольку числитель (напряжения
. Поскольку числитель (напряжения 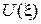 ) отстает по фазе от знаменателя (тока
) отстает по фазе от знаменателя (тока 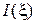 ), то входное сопротивление будет иметь емкостной характер:
), то входное сопротивление будет иметь емкостной характер:  .
.
В сечении линии с координатой 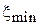 фаза коэффициента отражения
фаза коэффициента отражения 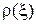 принимает, значения, кратные нечетному числу
принимает, значения, кратные нечетному числу  где m – целое число; коэффициент отражения
где m – целое число; коэффициент отражения 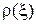 отрицателен и равен
отрицателен и равен  . Числитель и знаменатель дроби (4.4) снова вещественны (напряжение и ток линии синфазны), сопротивление, как и в сечениях
. Числитель и знаменатель дроби (4.4) снова вещественны (напряжение и ток линии синфазны), сопротивление, как и в сечениях  , вещественно и принимает минимальное значение, совпадающее численно с КБВ в линии (рис. 4.2, в):
, вещественно и принимает минимальное значение, совпадающее численно с КБВ в линии (рис. 4.2, в):
 (4.9)
(4.9)
Нетрудно установить, что в сечении, где  модуль сопротивления снова возрастает, а реактивная часть сопротивления имеет индуктивный характер
модуль сопротивления снова возрастает, а реактивная часть сопротивления имеет индуктивный характер  (рис. 4.2, б).
(рис. 4.2, б).
Короткозамкнутая линия
В технике СВЧ широко используется короткозамкнутые и разомкнутые отрезки линий. Из (4.3) следует, что коэффициент отражения на конце короткозамкнутой линии равен –1 (так как 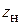 = 0). Тогда коэффициент отражения как функция
= 0). Тогда коэффициент отражения как функция 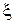 (4.5) представляется выражением
(4.5) представляется выражением
 (4.10)
(4.10)
Подставляя (4.10) в (4.1) и (4.2), легко получить распределения напряжения и тока в виде стоячих волн в короткозамкнутой линии:
 (4.11)
(4.11)
 (4.12)
(4.12)
Входное сопротивление линии можно найти, поделив  на
на  , из формул (4.11), (4.12):
, из формул (4.11), (4.12):
 (4.13)
(4.13)
Нормированное входное сопротивление короткозамкнутой линии
 (4.14)
(4.14)
Из формул (4.11)–(4.14) видно, что, изменяя 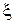 (расстояние от короткозамыкающей перемычки до любого сечения, где определяется входное сопротивление), можно получить на входе линии любые значения реактивного сопротивления (от
(расстояние от короткозамыкающей перемычки до любого сечения, где определяется входное сопротивление), можно получить на входе линии любые значения реактивного сопротивления (от  до
до  ). При фиксированной длине линии
). При фиксированной длине линии 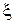 и переменной частоте входное сопротивление (4.14) меняется за счет волнового числа
и переменной частоте входное сопротивление (4.14) меняется за счет волнового числа  . Чем больше длина
. Чем больше длина 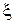 , тем резче меняется
, тем резче меняется  .
.
