В. В. Бабанов, Н.А. Масленников

В. В. Бабанов, Н.А. Масленников

СТРОИТЕЛЬНАЯ МЕХАНИКА

Расчетно-графические работы

Учебное пособие

Санкт-Петербург

УДК 624.04

Рецензенты:

д-р техн. наук, профессор А. А. Веселов (СПбГАСУ),

канд. техн. наук, доцент Ю. В. Бондарев (ООО «ТЕКТОН-СПб»)

Бабанов, В. В.

Строительная механика. Расчетно-графические работы: учеб. пособие / В. В. Бабанов, Н. А. Масленников; СПбГАСУ. – СПб., 2017. – 84 с.

ISBN

Приводятся методические указания к выполнению расчетно-графических работ и схемы заданий к ним. Указания составлены с учетом специфики обучения студентов направления 08.03.01 «Строительство», обучающихся по профилю – промышленное и гражданское строительство. Приведены примеры выполнения и оформления расчетно-графических работ.

Табл. 10. Ил. 50. Библиогр.: 12 назв.

Рекомендовано Учебно-методическим советом СПбГАСУ в качестве учебного пособия.

ISBN

Ó В. В. Бабанов, Н. А. Масленников, 2017

Ó Санкт-Петербургский государственный

архитектурно-строительный университет, 2017

ВВЕДЕНИЕ

При изучении курса строительной механики студенты выполняют 6 расчетно-графических работ (РГР):

в 1-м семестре обучения – РГР №№ 1, 2, 3;

во 2-м семестре обучения – РГР №№ 4, 5, 6.

Исходные данные для выполнения каждой работы студент выписывает из таблиц в соответствии со своим учебным шифром. Шифром являются три последние цифры номера зачетной книжки или студенческого билета. Например, если номер зачетной книжки 13816, то учебный шифр – 816, при этом 8 – первая, 1 – вторая, 6 – третья цифры шифра.

Работы, выполненные не по шифру, к проверке и защите не принимаются.

Решение задач необходимо сопровождать краткими пояснениями, всеми необходимыми расчетами и четкими схемами с указанием в необходимых случаях масштабов длин и сил.

Схемы заданий и методические указания

По их выполнению

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 1

РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ

НА ДЕЙСТВИЕ НЕПОДВИЖНОЙ НАГРУЗКИ

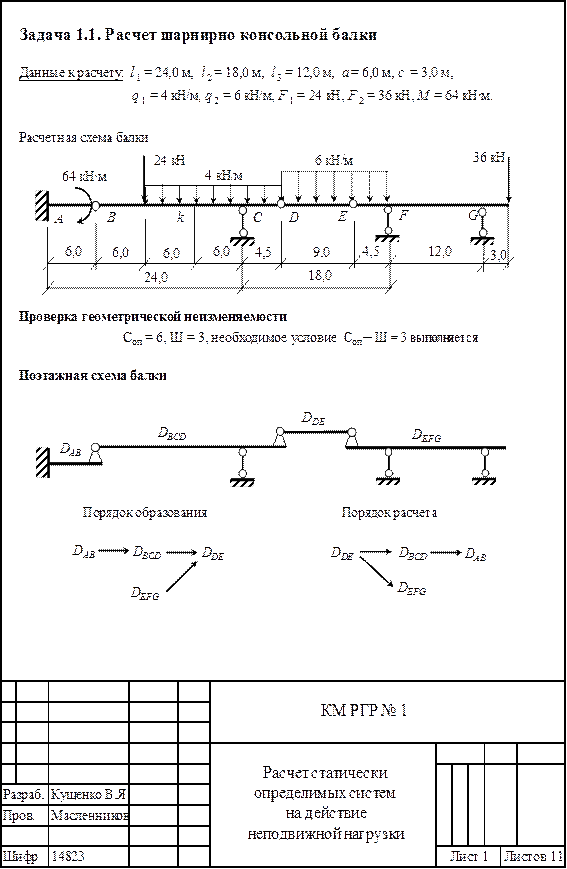
Задача 1.1. Расчет шарнирно-консольной балки

Литература: [1, с. 60–67], [3, c. 54–59], [4, c. 22–26],

[5, c. 98–101], [6, c. 12–21].

Исходные данные к задаче определяются по табл. 1.1 и схемам, представленным на рис. 1.1 и 1.2.

Последовательность расчета

1.1.1. Изобразить в масштабе схему балки с указанием размеров и действующих нагрузок.

1.1.2. Произвести анализ геометрической неизменяемости заданной схемы балки. Для этого использовать выражение, представляющее собой необходимое условие геометрической неизменяемости шарнирно-консольной балки Ш = С – 3, где Ш – число промежуточных шарниров; С – количество опорных связей, и выполнить анализ структуры взаимодействия отдельных дисков, построив поэтажную схему.

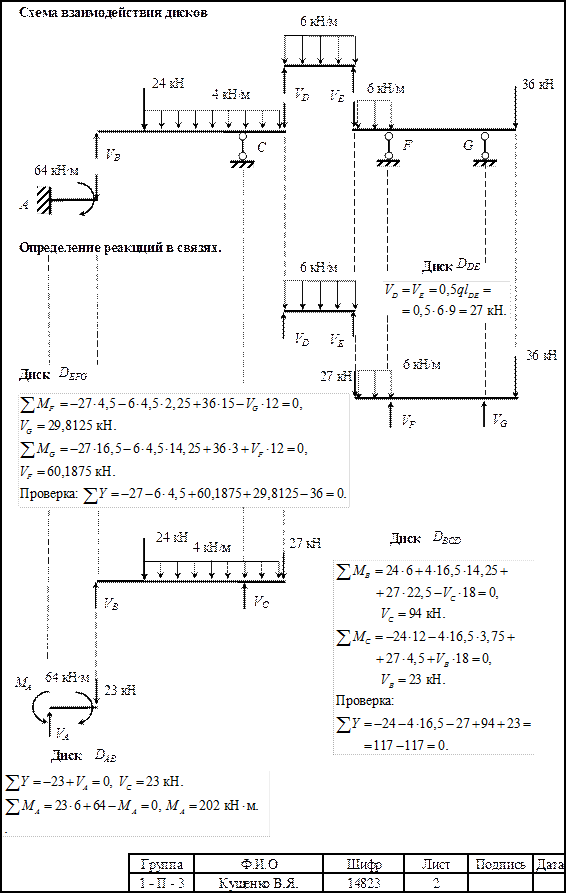
1.1.3. Показать схему взаимодействия отдельных дисков, расчленив заданную схему на главные и второстепенные балки, и определить реакции в связях от заданной нагрузки, составляя уравнения равновесия для каждого диска. Порядок рассмотрения дисков – сверху вниз по поэтажной схеме.

1.1.4. Показать схему взаимодействия отдельных дисков с найденными реакциями в связях.

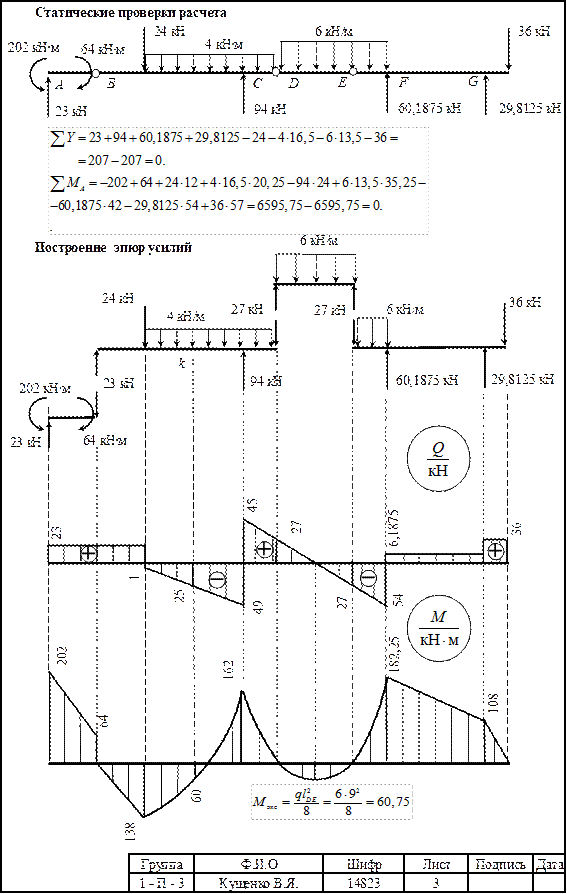
1.1.5. Произвести проверку правильности определения реакций в связях из условия равновесия всей расчетной схемы.

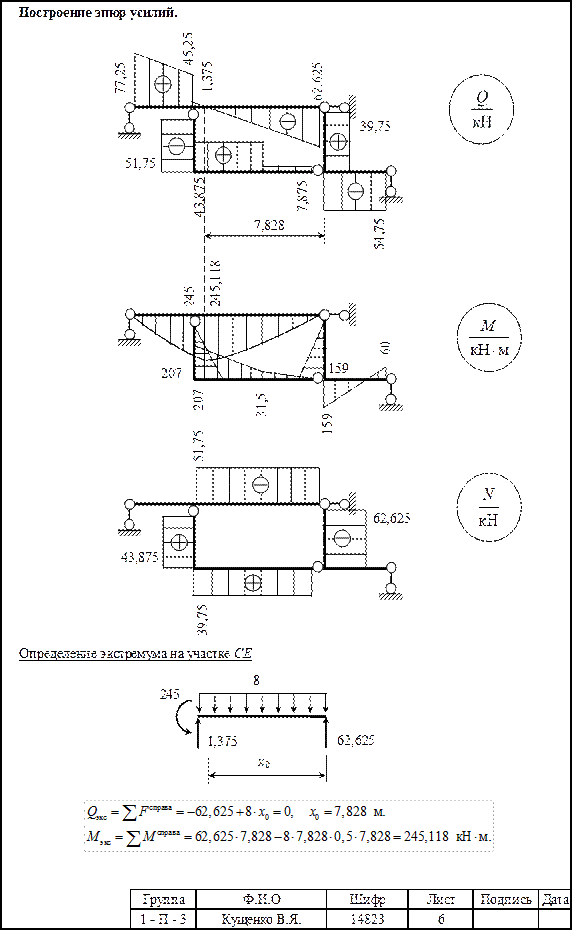
1.1.6. Построить эпюры поперечных сил и изгибающих моментов для отдельных дисков с объединением их для всей расчетной схемы.

Таблица 1.1

Исходные данные к задаче 1.1 РГР № 1

Первая цифра шифра	l1, м	q, кН/м	F, кН	Вторая цифра шифра	l2, м	l3, м	q1, кН/м	q2, кН/м	F1, кН	F2, кН	Третья цифра шифра (№ схемы)	a, м	b, м	c, м	d, м
		1,5
		2,5
		3,6					1,5
		2,4						1,5
		1,2					2,5
		1,8						2,5
		1,6

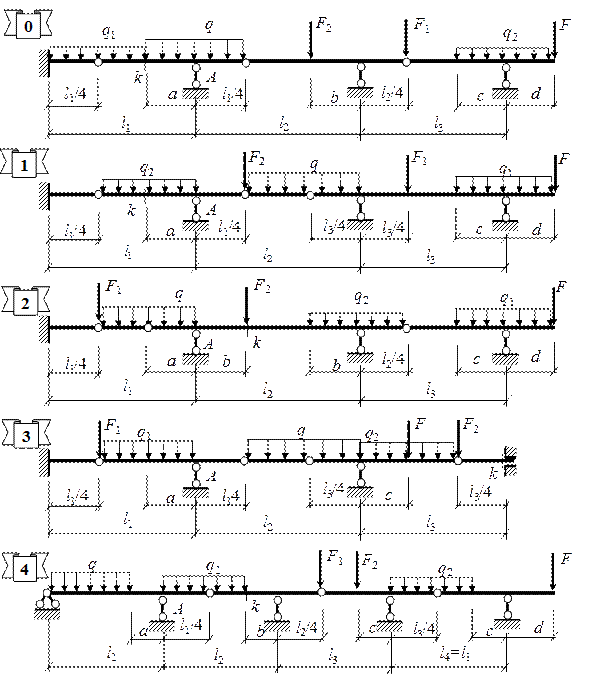
Рис. 1.1. Расчетные схемы 0 – 4 шарнирно-консольных балок

к задачам 1.1 и 2.1

1.1.7. Определить экстремальные значения изгибающих моментов в зонах действия распределенных нагрузок (при их наличии) и показать их значения и положения на эпюрах Q и M.

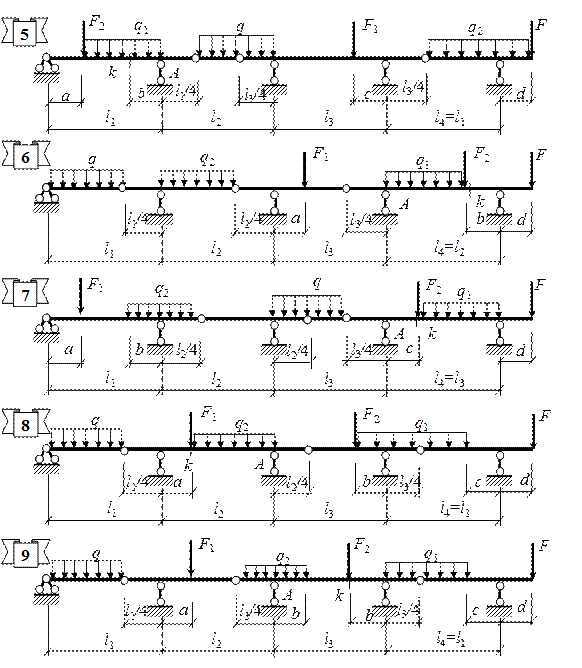
Рис. 1.2. Расчетные схемы 5 – 9 шарнирно-консольных балок

к задачам 1.1 и 2.1

1.1.8. Произвести проверку построения эпюр усилий. При правильном построении на каждом участке должно соблюдаться выполнение дифференциальных зависимостей

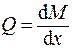и .

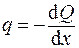Задача 1.2. Расчет рамы

Литература: [1, c. 113–124], [3, c. 63–66], [4, c. 38–42],

[5, c. 42–47], [6, c. 4–11, 49–53].

Исходные данные к задаче определяются по табл. 1.2 и схемам, представленным на рис. 1.3.

Таблица 1.2

Исходные данные к задаче 1.2 РГР № 1

Первая цифра шифра	M1, кН·м	M2, кН·м	Вторая цифра шифра	q1, кН/м	q2, кН/м	F1, кН	F2, кН	Третья цифра цифра (№ схемы)	l, м	h, м

Последовательность расчета

1.2.1. Произвести анализ геометрической неизменяемости заданной расчетной схемы.

Необходимым, но недостаточным условием геометрической неизменяемости, является выражение 3Д – 2Ш – С_оп = 0, где Д – количество дисков в расчетной схеме; Ш – количество простых шарниров или число связей, необходимых до полного защемления; С_оп – количество опорных связей.

Достаточное условие геометрической неизменяемости проверяется анализом геометрической структуры расчетной схемы.

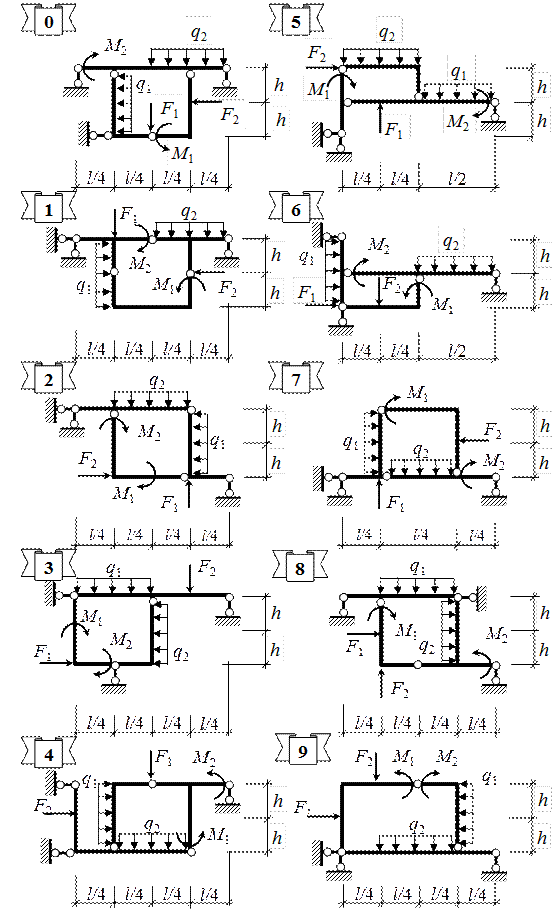Рис. 1.3. Расчетные схемы к задаче 1.2

1.2.2. Показать расчетную схему для определения реакций в опорных связях и определить эти реакции от действия заданной внешней нагрузки.

1.2.3. Показать расчетную схему для определения реакций внутренних связей. С этой целью замкнутый контур либо расчленяется по шарнирам на отдельные диски, либо при расчленении выделяется его трехшарнирная часть. Величины реакций в местах расчленения определяются из уравнений равновесия отдельных частей расчетной схемы.

1.2.4. Построить эпюры изгибающих моментов, поперечных и продольных сил. Эпюры можно построить сначала на отдельных частях расчетной схемы, а затем состыковать их в соответствии с заданной расчетной схемой.

1.2.5. Определить экстремальные значения изгибающих моментов в зонах действия распределенных нагрузок (при их наличии) и показать их значения и положение на эпюрах M и Q.

1.2.6. Произвести проверку построенных эпюр усилий. При правильном построении эпюр на каждом участке должны соблюдаться дифференциальные зависимост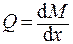и

и ,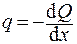

а любая отсеченная часть расчетной схемы и все ее узлы должны находиться в равновесии.

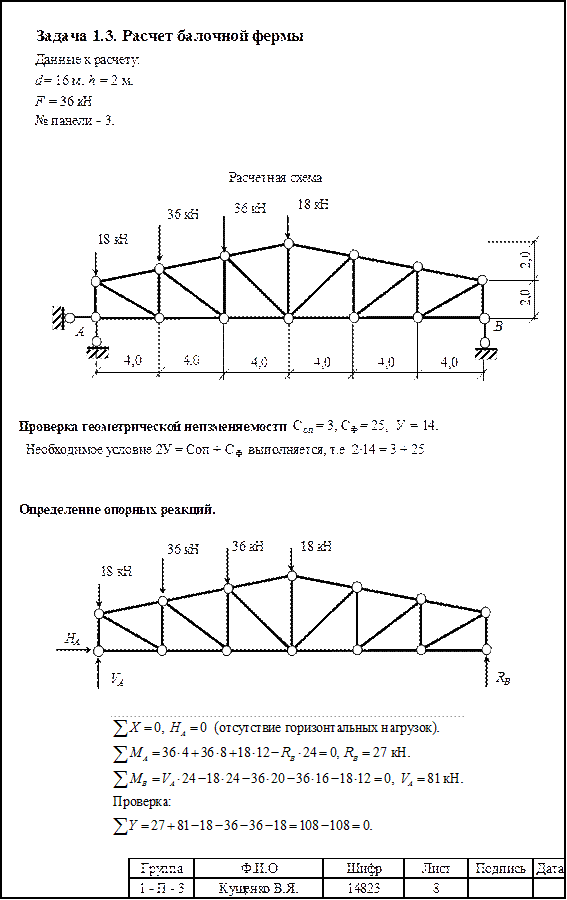
Исходные данные к задаче 1.3 РГР № 1

Первая цифра шифра	№ панели слева	Вторая цифра шифра	F, кН	Третья цифра шифра (№ схемы)	d, м	h, м
			1,2
			1,6			2,5
			2,0
			2,4
			2,8
			3,2			2,25
			3,6
			4,0
			4,4
			4,8			1,5

Последовательность расчета

1.3.1. Изобразить в масштабе расчетную схему фермы с указанием размеров и показать вертикальную узловую нагрузку, действующую по верхнему поясу.

1.3.2. Произвести анализ геометрической неизменяемости заданной схемы фермы.

Необходимое и достаточное условие геометрической неизменяемости простейших по структуре образования ферм заключается в выполнении условия С = 2У, где С – количество стержней фермы, включая опорные; У – количество узлов.

1.3.3. Аналитически определить опорные реакции.

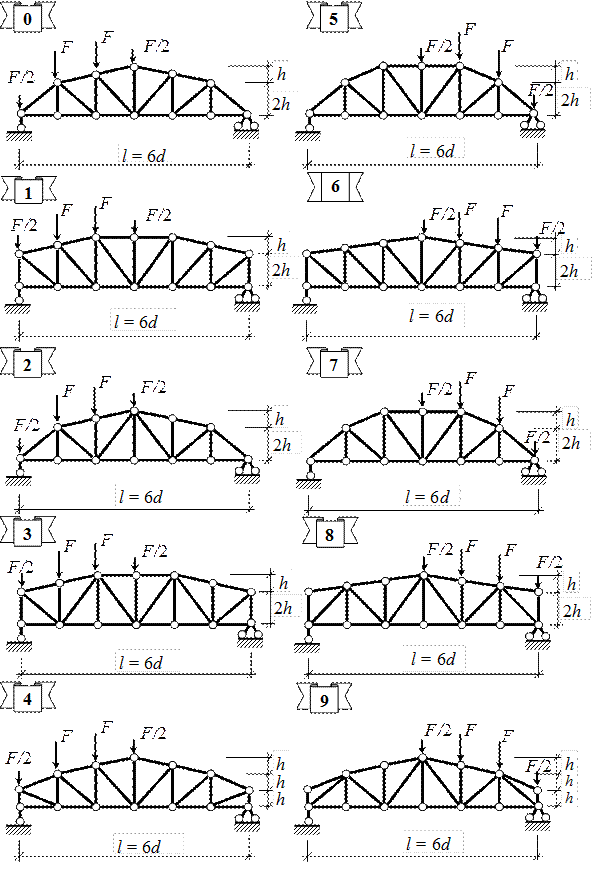
Рис. 1.4. Расчетные схемы к задачам 1.3 и 2.2

1.3.4. Построить диаграмму усилий для всей фермы и по ней определить усилия в всех стержнях фермы.

1.3.5. Аналитически, используя способ сечений, а при необходимости – способ вырезания узлов, определить усилия в стержнях заданной панели, включая левую и правую стойки.

1.3.6. Произвести сравнение аналитического и графического расчетов для стержней заданной панели (табл. 1.4).

Таблица 1.4

Исходные данные к РГР № 3

Первая цифра шифра	q1, кН/м	q2, кН/м	Вторая цифра шифра	F1, кН	F2, кН	Третья цифра шифра (№ схемы)	l, м	h, м	α

Последовательность расчета

3.1. Изобразить в масштабе расчетную схему рамы с указанием размеров и приложить заданную нагрузку.

3.2. Определить степень статической неопределимости рамы n_с = 3К – Ш, где n_с – степень статической неопределимости или число “избыточных” связей, К – число замкнутых контуров, а Ш – число простых шарниров в расчетной схеме, включая опорные, или число связей, необходимых для полного защемления всех узлов расчетной схемы.

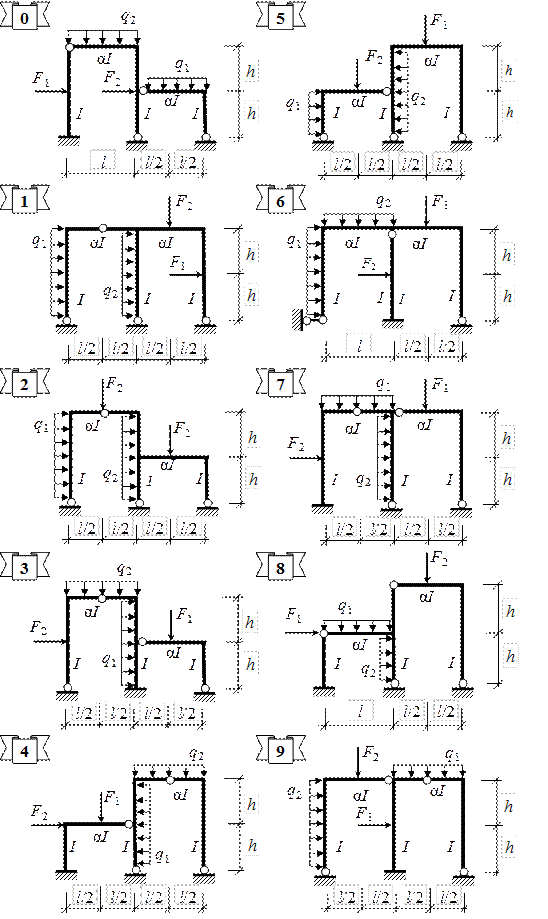
Рис. 3.1. Расчетные схемы к РГР № 3

3.3. Выбрать две статически определимые и геометрически неизменяемые основные системы путем удаления «лишних» связей, а вместо этих связей по их направлению показать соответствующие неизвестные X₁, X₂, … X_n. Более рациональную из этих основных систем использовать для дальнейшего расчета.

3.4. Записать в общем виде систему канонических уравнений метода сил применительно к данной расчетной схеме.

3.5. Показать расчетные схемы основной системы при последовательном загружении единичными безразмерными силами, приложенными по направлении удаленных связей. На расчетных схемах показать опорные реакции, определить их и построить эпюры изгибающих моментов .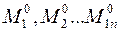

3.6. Показать расчетную схему основной системы при загружении ее внешней нагрузкой, определить опорные реакции и построить в основной системе эпюру изгибающих моментов .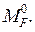

3.7. Определить коэффициенты при неизвестных системы канонических уравнений

,

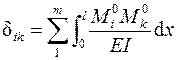где m - число участков интегрирования.

3.8. Определить свободные члены системы канонических уравнений

.

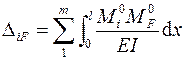Примечание. При перемножении простых эпюр (прямоугольники, треугольники) допускается применение правила Верещагина, а для перемножения более сложных эпюр рекомендуется воспользоваться формулой перемножения трапеций или вычислять интеграл Мора по формуле Симпсона.

3.9. Подставить найденные значения коэффициентов и свободных членов в систему канонических уравнений и решить ее относительно неизвестных X_i.

3.10. Построить эпюры изгибающих моментов от действительных значений реакций в удаленных связях. Для этого все ординаты эпюр 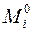(i = 1…n) умножаются на соответствующую величину X_i.

3.11. Построить эпюру изгибающих моментов в заданной расчетной схеме на основании принципа независимости действия сил

.

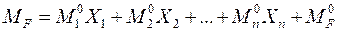3.12. Произвести деформационную проверку расчета. Для этого берется любая другая статически определимая основная система (например, вторая из выбранных в п. 3.3), в которой строится эпюра изгибающих моментов 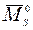от одновременного действия на нее всех единичных сил, приложенных по направлению удаленных связей. При правильно выполненном расчете должно выполняться условие

.

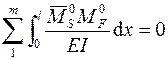Деформационная проверка будет выполняться и в том случае, если в приведенной формуле вместо 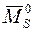использовать любую из эпюр 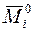поверочной основной системы.

Примечание. Деформационная проверка имеет смысл, если выбранная для проверки новая основная система дает эпюры 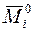, линейно независимые (не подобные) эпюрам 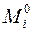, использованным в расчете.

3.13. Построить эпюру поперечных сил Q_F в заданной системе, используя дифференциальную зависимость Q_F = dM/dx.

3.14. Построить эпюру продольных сил N_F. Значения продольных сил в стержнях рамы определяются из условий равновесия ее узлов. К вырезанным узлам кроме неизвестных продольных сил прикладываются найденные поперечные силы и известные узловые нагрузки.

3.15. Произвести проверку равновесия системы. При выполнении данного пункта рекомендуется рассмотреть два сечения: сечение, проведенное по опорным связям (рассматривается равновесие всей рамы), и сечение, проведенное в любом месте расчетной схемы (рассматривается равновесие отсеченной части).

При правильном построении эпюр для любой отсеченной части системы должны выполняться уравнения равновесия 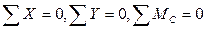, где c ─ любая точка на плоскости.

Исходные данные к РГР № 4

Первая цифра шифра	F1, кН	F2, кН	Вторая цифра шифра	q1, кН/м	q2, кН/м	Третья цифра шифра (№ схемы)	l, м	h, м	α

Последовательность расчета

4.1. Вычертить в масштабе расчетную схему рамы с указанием размеров, величин нагрузок и соотношений жесткостей.

4.2. Определить степень кинематической неопределимости рамы (число неизвестных метода перемещений) n_к = n_у + n_л , где n_у − число жестких узлов расчетной схемы, способных к повороту при ее деформации; n_л − число возможных линейных смещений всех узлов расчетной схемы.

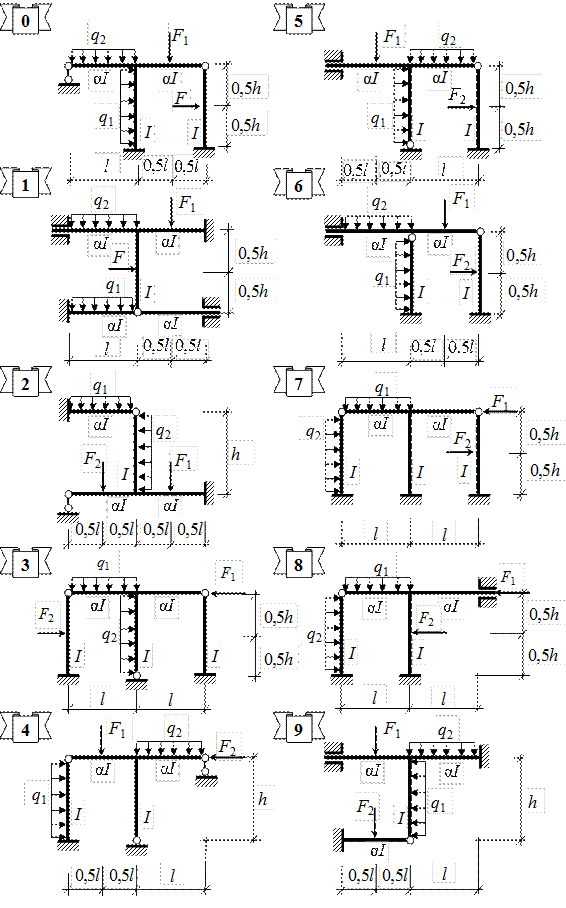
Рис. 4.1. Схемы заданий к РГР № 4

4.3. Получить основную систему метода перемещений, введя дополнительные связи по направлениям возможных углов поворота жестких узлов и линейных смещений всех узлов

Расчет в классической форме

4.4. Записать систему канонических уравнений метода перемещений в общем виде применительно к заданной схеме рамы.

4.5. Построить в основной системе метода перемещений деформированные схемы от последовательных единичных смещений по направлению дополнительных связей.

4.6. Используя таблицы реакций (пп. 1–4 прил. 1), построить в основной системе эпюры 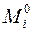от указанных в п.4.5 единичных смещений.

4.7. Используя таблицы реакций (пп. 5–8 прил. 1), построить в основной системе эпюру 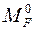от заданного загружения.

4.8. Определить коэффициенты при неизвестных (реакции в дополнительных связях от единичных смещений) и свободные члены (реакции в дополнительных связях от действия внешней нагрузки) системы канонических уравнений.

Указания:

· Реакции в дополнительных угловых связях определяются непосредственно из равновесия жесткого узла, в который введена угловая связь.

· Реакции в дополнительных линейных связях ортогональных рам определяются из условия равновесия отсеченной части основной системы. При этом сечения (сквозные или замкнутые) проводятся параллельно оси линейной связи через все стержни схемы, получившие деформации (см. п. 4.4) при смещении данной связи.

· Реакция в дополнительной связи считается положительной, если она направлена в сторону заданного в п. 4.4. смещения этой связи.

· Все схемы по определению реакций в дополнительных связях должны быть приведены на чертеже.

4.9. Записать систему канонических уравнений метода перемещений в численном виде и из ее решения найти неизвестные Z_i.

4.10. Определить изгибающие моменты в основной системе от действительных смещений по направлению дополнительных связей (построить эпюры) и на основании принципа независимости действия сил построить эпюру изгибающих моментов в заданной расчетной схеме

.

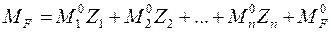4.11. Произвести проверки правильности построения эпюры :

·Для каждого жесткого узла заданной расчетной схемы должно выполняться уравнение равновесия.

· Для всей рамы должна выполняться деформационная проверка расчета. Для этого выбирается любая наиболее простая статически определимая основная система, получаемая из заданной путем удаления лишних связей. В выбранной статически определимой основной системе строится суммарная эпюра изгибающих моментов 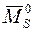от единичных сил, приложенных по направлению удаленных связей. Проверка считается выполненной, если

.

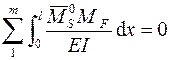4.12. Построить эпюру поперечных сил в заданной расчетной схеме на основании дифференциальной зависимости Q_F = dM/dx.

4.13. Определить продольные силы во всех стержнях расчетной схемы из условия равновесия ее узлов и построить эпюру N_F.

4.14. Произвести статическую проверку расчета: любая отсеченная часть расчетной схемы или вся схема, отсеченная от опор, под действием внутренних и внешних сил должна находиться в равновесии, т.е. должны выполняться три уравнения равновесия 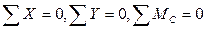(c– любая точка на плоскости).

Для выполнения этой проверки рекомендуется рассмотреть два случая:

· Равновесие всей расчетной схемы, отсеченной от опор.

· Равновесие любой отсеченной части расчетной схемы

Расчет в матричной форме[1]

4.15. Вычертить основную систему метода перемещений (п. 4.2) и на ней показать порядок обхода стержней расчетной схемы и пронумеровать расчетные сечения в соответствии с намеченным обходом.

4.16. Составить матрицы жесткости отдельных стержней рамы:

· для участков c одним расчетным сечением

;

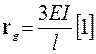· для участков с двумя расчетными сечениями

.

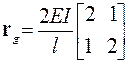4.17. Составить квазидиагональную матрицу жесткости не объединенных элементов 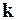(m x m), где m – число расчетных сечений рамы. В общем виде эта матрица имеет вид

.

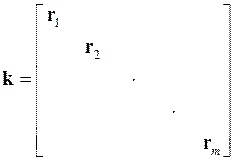4.18. По деформированным схемам, построенным в основной системе от единичных смещений по направлению дополнительных связей (п. 4.4), определить углы поворота расчетных сечений и составить матрицу преобразования деформаций 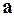порядка (m x n), где n – число неизвестных метода перемещений.

4.19. По эпюре (см. п. 4.6) составить матрицу усилий в основной системе метода перемещений 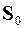(m´p), где p – число вариантов загружения (для данной РГР p = 1).

4.20. Составить матрицу 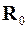свободных членов системы канонических уравнений (n x p), используя результаты расчета в классической форме (см. п. 4.7).

4.21. Выполнить ниже перечисленные матричные операции.

· Транспонировать матрицу .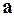

· Получить матрицу усилий в расчетных сечениях основной системы от единичных смещений по направлению дополнительных связей

.

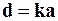· Получить матрицу коэффициентов при неизвестных

.

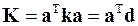· Выполнить обращение матрицы 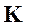и произвести проверку обращения

,

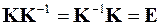где 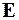– единичная матрица.

· Определить неизвестные метода перемещений

.

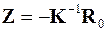· Определить усилия в основной системе метода перемещений от действительных смещений по направлению дополнительных связей

.

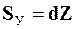· Получить матрицу усилий в заданной расчетной схеме

.

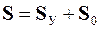· Сравнить значения элементов матрицы 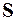, с усилиями, полученными классической формой расчета (п. 4.10).

4.22. Произвести проверку правильности произведенного расчета. Для этого по эпюре 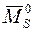(см. п. 4.11) составить матрицу усилий .

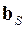Деформационная проверка расчета в матричном виде будет иметь вид:

,

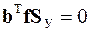где 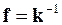─ матрица податливости необъединенных элементов расчетной схемы.

РАСЧЕТНО-ГРАФИЧЕСКАЯ № 5

ДИНАМИЧЕСКИЙ РАСЧЕТ ПЛОСКОЙ РАМЫ

С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ НА ДЕЙСТВИЕ ВИБРАЦИОННОЙ НАГРУЗКИ

Литература: [2, c. 178–197], [8, c. 124–220], [9, c. 3–61],

[11, c. 54–65, 69–82].

Исходные данные к работе определяются по табл. 5.1 и схемам, представленным на рис. 5.1.

Таблица 5.1

Исходные данные к РГР № 5

Первая цифра шифра	m, т	β	Вторая цифра шифра		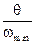α	F1, кН	F2, кН	Третья цифра шифра (№ схемы)	l, м	h, м	EI1, кН·м2
	0,5			0,5	1,5
	0,6	1,5		0,55
	0,7			0,6	2,5
	0,8	2,5		0,65
	0,9			0,7	1,5
	1,0			0,68
	1,1	1,5		0,8	2,5
	1,2			0,72
	1,3	2,5		0,66	3,5
	1,4			0,58

Примечание. В таблице приведены амплитудные значения вибрационной нагрузки F_i (t) = F_i sin θt.

Последовательность расчета

5.1. Вычертить в масштабе заданную расчетную схему рамы с указанием размеров, величин масс, вибрационной нагрузки и соотношения жесткостей стержней.

5.2. Определить число степеней свободы сосредоточенных масс заданной расчетной схемы.

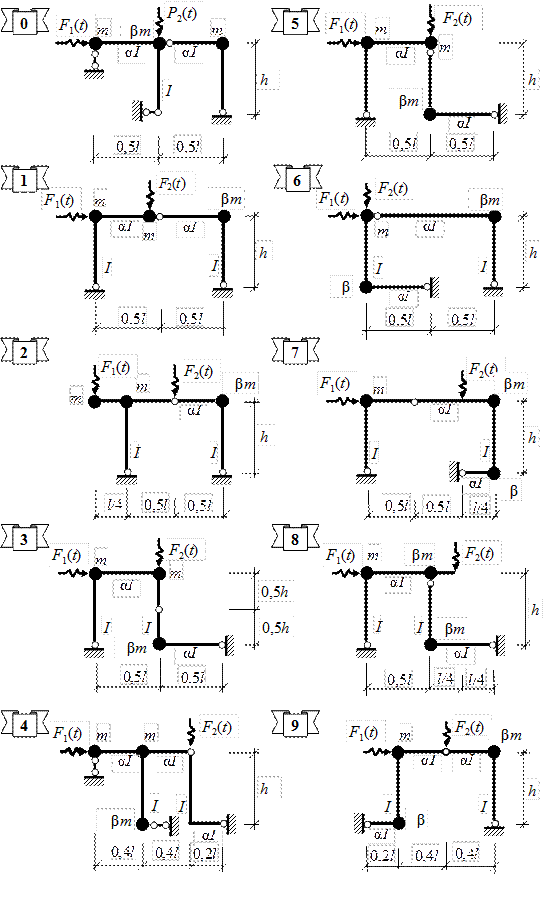
Рис. 5.1. Схемы заданий к РГР № 5

5.3. Показать расчетную схему рамы при действии амплитудных значений инерционных сил и вибрационной нагрузки.

5.4. Записать в общем виде уравнение частот свободных колебаний применительно к заданной расчетной схеме.

5.5. По направлению возможных смещений масс последовательно приложить единичные силы и от действия каждой из них построить эпюры изгибающих моментов M_i.

5.6. Определить коэффициенты уравнения частот

,

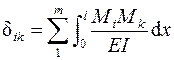где m – число участков интегрирования.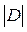

5.7. Составить уравнение частот в численном виде.

5.8. Определить корни частотного уравнения l_i (i = 1 … n) и произвести проверки правильности его решения:

,

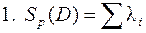где S_p (D) – след (сумма главных коэффициентов) матрицы, составленной из коэффициентов частотного уравнения; 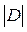– величина определителя этой матрицы

5.9. Определить частоты и периоды свободных колебаний масс.

5.10. Вычислить относительные амплитуды масс и построить формы колебаний для каждой частоты.

5.11. Из определенного в п. 5.7 спектра частот свободных колебаний выявить наименьшее значение ω_min и определить круговую частоту вынужденных колебаний по заданному в табл. 5.1 соотношению.

5.12. Показать расчетную схему рамы при действии на нее амплитудных значений нагрузок и инерционных сил.

5.13. Записать в общем виде систему канонических уравнений для определения амплитудных значений инерционных сил применительно к заданной расчетной схеме.

5.14. Построить в заданной расчетной схеме эпюру изгибающих моментов M_F от действия амплитудных значений вибрационной нагрузки.

5.15. Определить главные коэффициенты системы канонических уравнений

.

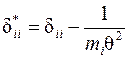Побочные коэффициенты системы канонических уравнений имеют те же значения, что и в уравнении частот.

5.16. Определить свободные члены системы канонических уравнений

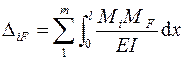
5.17. Записать систему канонических уравнений в численном виде и из ее решения определить амплитудные значения инерционных сил J_i.

5.18. Построить динамическую эпюру изгибающих моментов

M_дин = M₁ J₁ + M₂ J₂ + …+M_n J_n + M_F.

5.19. Определить амплитуды масс a_i = J_i/m_i∙θ² и построить деформированную схему рамы при вынужденных колебаниях.

Исходные данные к РГР № 6

Первая цифра шифра	EI1, кН·м2	α	Вторая цифра шифра	l1, м	β	Третья цифра шифра (№ схемы)	l2, м	h1, м	h2, м
		1,5			1,21			4,2	3,2
		2,0			0,81			3,6	3,0
		1,8			1,44			4,8	3,3
		2,4			2,89			2,7	2,7
		2,7			2,56			3,3	3,3
		3,0			1,69			4,0	3,6
		3,3			1,96			4,5	4,0
		3,6			0,64			3,6	2,7
		4,2			0,49			5,4	4,0
		2,2			3,24			5,0	3,6

Последовательность расчета

6.1. Вычертить в масштабе расчетную схему рамы с указанием размеров, нагрузки и других данных к расчету.

6.2. Пронумеровать все стержни расчетной схемы, определить их относительные жесткости i_k = EI_k /l_k (k – номер стержня) и выразить их через общий множитель i₀, приняв за него величину относительной жесткости любого из стержней рамы.

6.3. Записать для всех сжатых стержней выражения их критических параметров

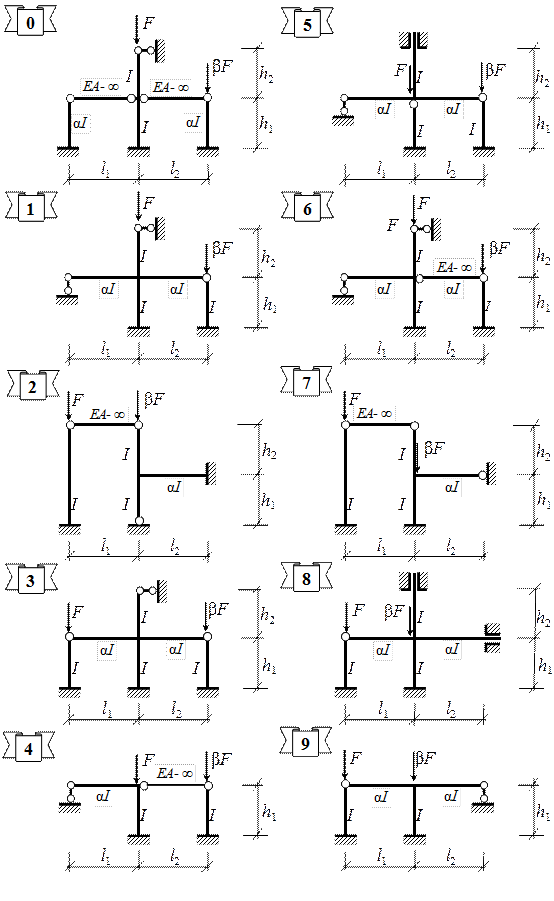
Рис. 6.1. Схемы заданий к РПР № 6

,

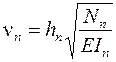где n – номер сжатого стержня; N_n – величина сжимающей силы в этом стержне; EI_n – его жесткость при изгибе; h_n – длина сжатого стержня.

Все параметры n_n выразить через единый n, принимая за последний любой из параметров n_n.

6.4. Выбрать основную систему метода перемещений путем введения в заданную расчетную схему дополнительных угловых и линейных связей по направлению возможных угловых и линейных смещений узлов.

6.5. Составить уравнение устойчивости в общем виде применительно к заданной расчётной схеме.

6.6. Построить в основной системе эпюры изгибающих моментов от единичных смещений по направлениям введенных дополнительных связей, используя таблицы реакций прил. 1 и 2.

6.7. С помощью построенных эпюр определить реакции в дополнительных связях от заданных единичных смещений и представить уравнение устойчивости в развернутом виде.

6.8. Решить уравнение устойчивости путем подбора наименьшего критического параметра n_cr при помощи таблиц трансцедентных функций (прил. 3 и 4) или на ПК при помощи учебной программы BUCLING.

6.9. Определить критические силы F_cr и расчетные длины l₀ для всех сжатых стоек расчетной схемы по найденным значениям критических параметров n_n,cr по формулам:

.

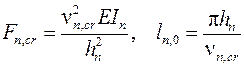Порядок работы по учебной программе

«BUCLING’

1. Открыть BUCLING.exe.

2. В открывшемся окне выбрать ВАША ФУНКЦИЯ, нажать ENTER.

3. В появившемся окне ознакомиться с принятыми в программе обозначениями трансцедентных функций и нажатьENTER.

4. В следующем появившемся окне набрать левую часть уравнения устойчивости.

5. Сохранить записанное уравнение F2.

6. Нажать ESC.

7. В следующем появившемся окне ввести последовательно интервалы поиска критического параметра и точность (шаг) поиска:

0.0 ENTER 6.28 ENTER 0.01 ENTER.

8. На появившемся графике выбрать значение наименьшего критического параметра, отмеченного красным цветом.

9. Нажать ESC.

10. В появившемся окне выбрать ЗАВЕРШЕНИЕ РАБОТЫ и выйти из программы.

Примеры выполнения и оформления расчетно-графических работ