Решение нелинейного уравнения
МЕТОДОМ НЬЮТОНА
II. ЦЕЛЬ РАБОТЫ
Приобретение навыков отыскания приближенных значений действительных корней уравнения методом Ньютона.
III. ТЕОРЕТИЧЕСКАЯ СПРАВКА
Требуется найти корни уравнения
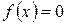, (1)
где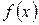 
- дифференцируемая функция.
Если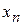 
есть некоторое приближение к корню 
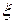, а 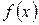имеет непрерывную производную, то уравнение (1) можно преобразовать следующим образом:
,
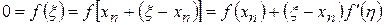где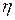 
- точка, лежащая между 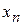и .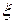
Приближенно заменяя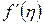 
на значение в известной точке 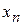, получим такой итерационный процесс:
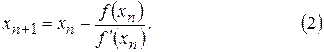
Геометрически этот процесс означает замену на каждой итерации графика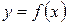 
касательной к нему.
Метод Ньютона можно рассматривать как частный случай метода итераций, если положить
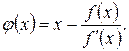
Тогда
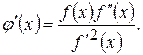
При произвольном начальном приближении итерации сходятся, если всюду на рассматриваемом интервале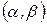 
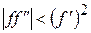(чтобы 
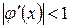, причем 
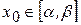). В противном случае сходимость будет не при любом начальном приближении, а только в некоторой окрестности корня.
Отметим еще достаточное условие сходимости итераций: есл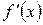и 
и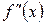 
отличны от нуля и сохраняют определенные знаки на 
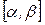, то исходя из начального приближения 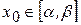, удовлетворяющего неравенству 
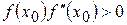, получим методом Ньютона значение корня с любой степенью точности. Т.о., в качестве исходной точки 
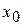следует выбирать тот конец 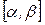, для которого 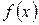и 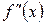имеют одинаковые знаки. Если взять такое 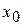, что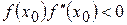 
, то мы можем не прийти к корню 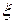, если только 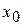не очень хорошее.
Оценим скорость сходимости метода Ньютона. Справедлива оценка
,
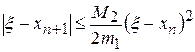где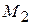 
- наибольшее значение 
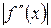на ,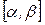 
; 
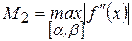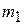- наименьшее значение 
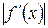на ,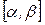 
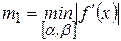. Отсюда видно, что погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Самый неблагоприятный случай для метода Ньютона, когда 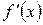становится малой вблизи корня. Чтобы не было потери точности, отношение 
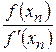надо вычислять достаточно аккуратно. К остальным погрешностям расчета метод Ньютона хорошо устойчив.
IV. ЗАДАНИЕ
Найти методом Ньютона один из действительных корней уравнения 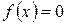с точностью 
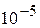. Варианты заданий приведены в лабораторной работе № 6.
IV. Оформление отчета
В отчете должны быть представлены:
1. Название работы.
2. Постановка задачи.
3. Описание алгоритма (метода) решения.
4. Текст программы с описанием.
5. Результаты работы программы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.
2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.
3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.
4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. 350 с.
Лабораторная работа № 9
ПРИМЕНЕНИЕ ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЫ
ЛАГРАНЖА
I. ЦЕЛЬ РАБОТЫ
Приобретение навыков использования интерполяционных многочленов.
II. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Пусть функция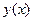 
задана таблично, т.е. известны ее значения в 
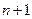точках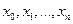 
( 
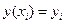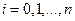). (1)
Построим многочлен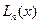 
степени 
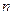такой, чтобы выполнялись интерполяционные условия
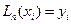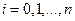( ). (2)
Сначала построим полином степени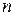 
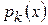, такой, что
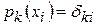, (3)
где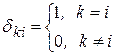 
- символ Кронекера.
Так как 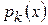обращается в нуль в 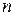точках 
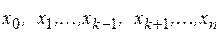, то он имеет вид
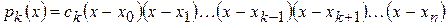, (4)
где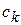 
- постоянный коэффициент.
Полагая в формуле (4)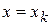 
и учитывая, что 
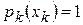, получим
.
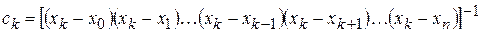Подставив этот коэффициент в (4), находим
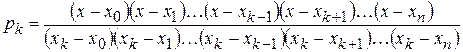. (5)
Теперь построим многочлен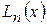 
, который имеет вид
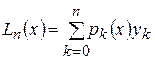. (6)
Степень 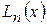, как видно из (5) и (6), не выше 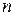. Кроме того, на основании (2)
,
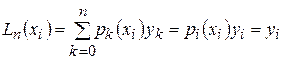что согласуется с (2)
Интерполяционный многочлен 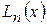называется многочленом Лагранжа и имеет вид
.
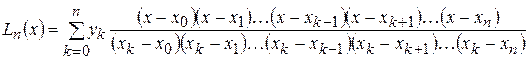Теперь считаем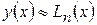 
.
Для абсолютной погрешности интерполяционного многочлена Лагранжа справедлива оценка
,
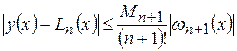где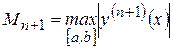 
;
.
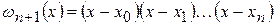III. ЗАДАНИЕ
Дана таблица значений функции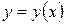 
| x | 3,5 | 4,1 | 4,3 | |
| y | N+k | N+2k | N-k | N |
Здесь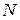 
- номер фамилии студента в журнале группы; 
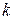- последняя цифра номера группы.
Построить интерполяционный многочлен Лагранжа. Вычислить с его помощью значения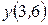 
; 
; 
.
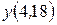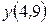IV. Оформление отчета
В отчете должны быть представлены:
1. Название работы.
2. Постановка задачи.
3. Описание алгоритма (метода) решения.
4. Текст программы с описанием.
5. Результаты работы программы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.
2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.
3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.
Лабораторная работа № 10