Передаточная функция разомкнутой системы

Логарифмические частотные характеристики

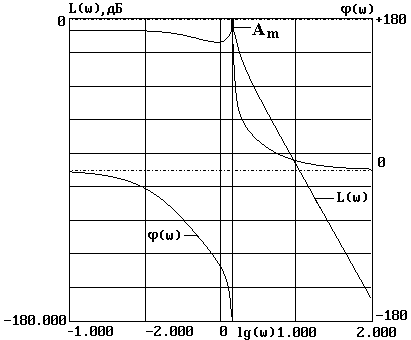
Запас устойчивости по амплитуде на частоте 1.445 рад/с равен А_м = 0.508 или 5.882 дБ, запас устойчивости по фазе равен максимальному значению φ_м = 180 град, поскольку ЛАЧХ отрицательна во всем диапазоне частот, частота среза отсутствует. Значения запасов удовлетворяют стандартным требованиям к САР.

Содержание отчета

Отчет к лабораторной работе должен содержать название, цель работы, структурную схему системы с указанием точек размыкания контура обратной связи, передаточную функцию разомкнутой системы, окончательный вид ЛФЧХ и ЛАЧХ в соответствующем масштабе с необходимыми графическими построениями, найденные значения запасов устойчивости по амплитуде и фазе с учетом единиц измерения – на графике и отдельно, с указанием частот, которым соответствуют эти запасы.

К защите необходимо знать формулировки критерия Найквиста в обычном и логарифмическом виде, особенности его применения, методику построения асимптотической ЛАЧХ и расчета необходимых для этого параметров, единицы измерения ЛЧХ, нормы запасов устойчивости при их оценке по АФЧХ и ЛЧХ.

Литература

1 Ерофеев А.А. Теория автоматического управления. – 2-е изд., перераб. и доп. – СПб. : Политехника, 2005. – 302 с.

2 Бороденко В.А. Практический курс теории линейных систем автоматического регулирования. – Павлодар : Изд-во Кереку, 2007. – 260 с.

3 Сборник задач по теории автоматического регулирования и управления: Под ред. В.А. Бесекерского. – 5-е изд. – М.: Наука, 1978. – 512 с.

4 Электрические системы. Математические задачи электроэнергетики: Учебник для студентов вузов / Под ред. В. А. Веникова – 2-е изд., перераб. и доп. - М.: Высш. школа, 1981. - 288 с.

Приложение А

(справочное)

Структурные преобразования

Для анализа или синтеза систему представляют структурной схемой, состоящей из звеньев, ветвей, узлов и сумматоров. Звено или блок обычно изображается прямоугольником, имеющим вход и выход с указанием функции преобразования внутри. Узлы (места разветвления сигнала) обозначаются на графической схеме точкой с диаметром 1,5-2 мм. Ветвь (связь) представляется линией со стрелкой в конце, отображающей направление движения сигнала. Сумматоры (элементы сравнения) представляют собой места схождения сигналов.

Они обозначаются либо пустым кружком среднего размера (крупнее уз­ла), либо крупным кружком, перечерк­нутым крест накрест прямыми линиями.

Сумматор, как правило, имеет не более трех входов, не более одного выхода и коэффициент передачи k = 1. Все входы сумматора независимы друг от друга. Если на входе сумматора производится из­менение знака сигнала (инвертирование), т. е. по этому входу коэф­фициент сумматора равен минус единице, вход называется инверти­рующим, а сумматор – элементом сравнения. Такой вход сумматора обозначается минусом для изображения в виде пустого кружка, и за­тушеванным сектором для обозначения в виде крупного кружка.

Обычно при известных функциях передачи отдельных звеньев требуется найти эквивалентную передаточную функцию (ПФ) объединения звеньев (объекта, регулятора), либо всей системы в целом. Для этого используют правила структурных преобразований.

1) Последовательное соединение звеньев.

Эквивалентная передаточная функция последовательно соеди­ненных звеньев равна произведению передаточных функций этих звеньев.

2) Параллельное соединение звеньев.

Эквивалентная передаточная функция параллельно соединенных звеньев равна сумме передаточных функций этих звеньев (с учетом знака входа сумматора на пути сигнала).

3) Соединение с обратной связью (встречно-параллельное).

Эквивалентная передаточная функция соединения с обратной связью равна дроби, в числителе которой записана ПФ звена на пря­мом пути от входа к выходу, а в знаменателе – единица минус произведение ПФ звеньев по замкнутому контуру обратной связи (ЗКОС).

4) Перенос воздействий в системах с перекрестными связями (правило структурных преобразований, применяющееся, если система включает соединения смешанного типа – не чисто последовательные, и не чисто параллельные).

Чтобы результирующая система не изменилась, в цепь перено­симого воздействия вводят фиктивное звено с ПФ, равной переда­точной функции потерянных, либо обратной передаточной функции приобретаемых при переносе звеньев.

Смысл правила состоит в том, что любые изменения по сравне­нию с исходной схемой, появляющиеся в системе после ее преобразо­вания, не должны влиять на результирующую передаточную функ­цию.

5) Правило Мейсона.

Правило рассматривает систему как ориентированный граф и позволяет описать ее всю сразу, без преобразований по отдельным фрагментам.

Передаточная функция системы образует дробь, числитель которой равен сумме произведений ПФ прямых путей на совокупные определители ЗКОС, не касающихся этих путей, а знаменатель – единица минус сумма произведений определителей несоприкасающихся ЗКОС и передаточных функций общих ЗКОС.

Определитель ЗКОС равен разности единицы и произведения ПФ звеньев по контуру, например, Δ₁₂=1-(-W₁W₂)=1+W₁W₂.

При составлении полинома числителя передаточной функции W_zx показанной системы вычисляем ПФ прямого пути от входа х к выходу z (равна коэффициенту передачи сумматора 1) и проверяем, что все замкнутые контуры обратной связи касаются этого прямого пути. Данное условие не выполняется, поэтому нужно умножить ПФ прямого пути на определитель несоприкасающегося с ним ЗКОС Δ₂₃=1-W₂W₃. При составлении полинома знаменателя передаточной функции убеждаемся, что все замкнутые контуры обратной связи касаются друг друга (имеют общий участок), тогда единица на все контуры одна. Следовательно, записываем в знаменателе единицу и далее плюс-минус произведения ПФ звеньев по каждому ЗКОС. Окончательно