Операции над комплексными числами.
1. Если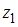 
и 
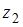– корни квадратного уравнения 
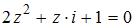, то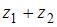 
равно …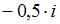 
2. Значение выражения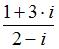 
равно …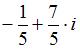 
3. Есл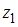и и 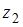– корни квадратного уравнения 
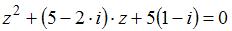, то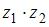 
равно …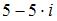 
4. . Если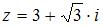 
, то все значения квадратного корня из 
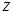равны … 
, 
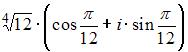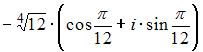
5. Сумма комплексных чисел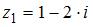 
и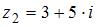 
равна …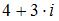 
6. Дано комплексное число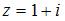 
. Тогда 
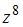равно …(16)
7. Частное от деления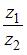 
двух комплексных чисел 
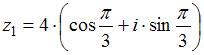и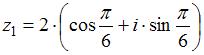 
равно …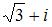 
Области на комплексной плоскости.
1.Все точки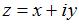 
комплексной плоскости, принадлежащие множеству 
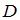, изображенному на рисунке:
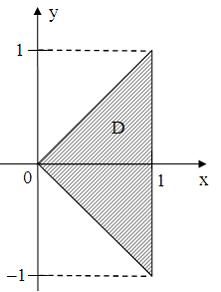удовлетворяют условию …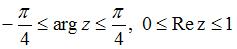 
2. Все точки 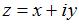комплексной плоскости, принадлежащие множеству 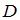, изображенному на рисунке:
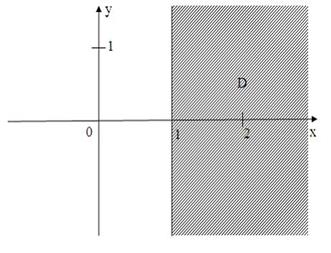удовлетворяют условию …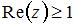 
3. Все точки 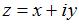комплексной плоскости, принадлежащие множеству 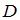, изображенному на рисунке:
удовлетворяют условию …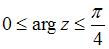 
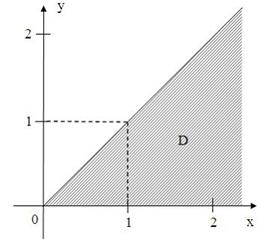
4. Все точки 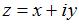комплексной плоскости, принадлежащие множеству 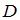, изображенному на рисунке:
удовлетворяют условию …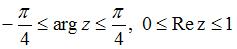
5.Все точки 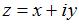комплексной плоскости, принадлежащие множеству 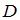, изображенному на рисунке,
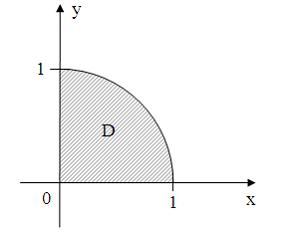удовлетворяют условию …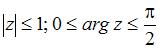 
6. Все точки 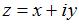комплексной плоскости, принадлежащие множеству 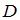, изображенному на рисунке:
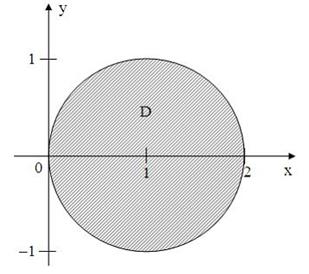удовлетворяют условию …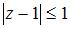 
7. Все точки 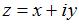комплексной плоскости, принадлежащие множеству 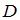, изображенному на рисунке,
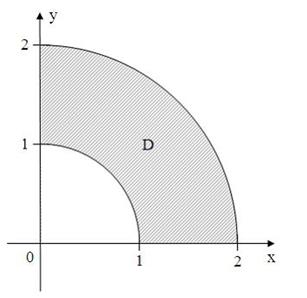удовлетворяют условию …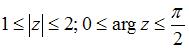 
8. Все точки 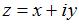комплексной плоскости, принадлежащие множеству 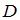, изображенному на рисунке:
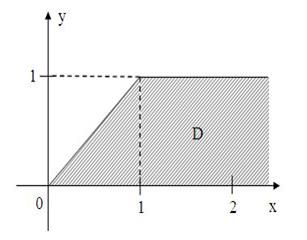удовлетворяют условию …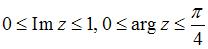 
9. Все точки 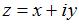комплексной плоскости, принадлежащие множеству 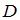, изображенному на рисунке,
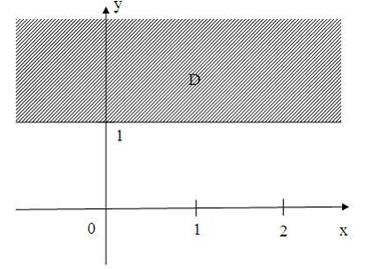удовлетворяют условию …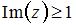 
10. Все точки 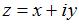комплексной плоскости, принадлежащие множеству 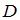, изображенному на рисунке,
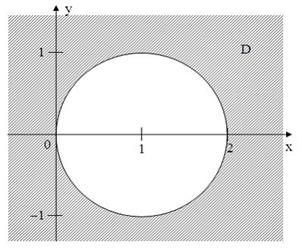удовлетворяют условию …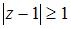 
Дифференцирование функции комплексного переменного.
1. Есл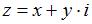и 
и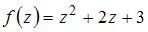 
, то производная функции 
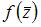имеет вид … 
( 
)
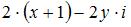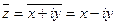2. Если 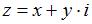и 
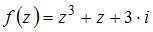, то мнимая часть производной этой функции 
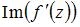имеет вид …( 
)
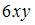3. Есл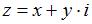и и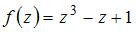 
, то действительная часть производной этой функции 
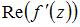имеет вид …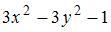 
4. Значение производной функции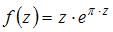 
в точке 
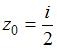равно …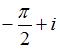 
5. Если 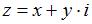и 
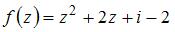, то мнимая часть производной этой функции 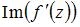имеет вид …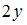 
6. Если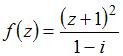 
, то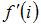 
равно …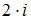 
7. Значение производной функции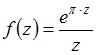 
в точке 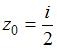равно …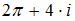 
8. Значение производной функции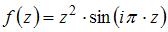 
в точке 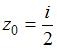равно …( 
)
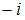ДЕ 7. Гармонический анализ
ПРИМЕРЫ
Периодические функции
1. Период функции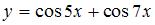 
равен … 
2. Наименьший положительный период функции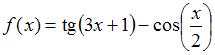 
равен …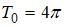 
3. Наименьший положительный период функции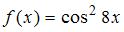 
равен …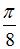 
4. Период функции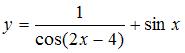 
равен …
5. Основной период функции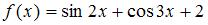 
равен … .
6. Период функции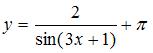 
равен …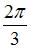 
7. Основной период функции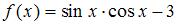 
равен …( 
)
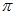Гармонические колебания
1.Точка совершает гармонические колебания вдоль оси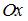 
по закону 
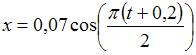. Тогда период колебаний равен …(4)
2. Точка совершает гармонические колебания вдоль оси 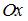по закону: 
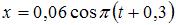. Тогда начальная фаза колебаний равна …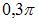 
3. Максимальное значение скорости точки, совершающей гармонические колебания, с амплитудой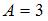 
, и угловой частотой 
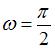, равно …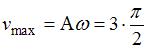 
4. Гармонические колебания с частотой 0,5 амплитудой колебания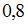 
и начальной фазой, равной нулю, описывается уравнением …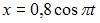 
5. Модуль скорости точки, совершающей гармонические колебания, с амплитудой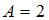 
, угловой частотой 
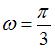и начальной фазой 
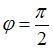, в момент времени 
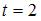равен …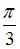 
6. Амплитуда гармонических колебаний равна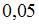 
, период равен 4 и начальная фаза равна 
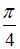. Тогда смещение колеблющейся точки от нулевого положения при 
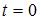равно … 