Вариационные задачи с подвижными границами

В предыдущих лекциях при исследовании функционала

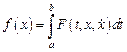
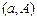предполагалось, что граничные точки и 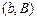заданы. Подобное предположение не всегда выполняется для многих интересных и практически важных вариационных задач. Рассмотрим в качестве примера задачу навигации.

Задача навигации

В этой задаче рассматривается река ширины 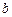с прямыми параллельными берегами. Считая один берег реки совпадающим с осью 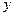, введем скорость течения реки 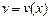. Лодка с постоянной скоростью

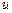( – величина скорости, 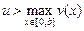), за кратчайшее время должна пересечь реку, отчалив из точки 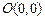(рис.1).

Обозначим через 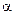угол, который образует вектор скорости лодки с положительным направлением оси 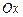. Тогда реальная скорость движения лодки в момент времени 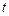определяется равенствами

, .

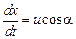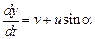Отсюда

,

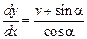что позволяет выразить 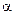через :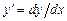

,

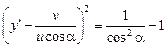откуда

.

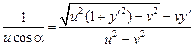Для времени пересечения реки находим

.

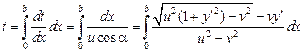Последний интеграл должен быть минимизирован за счет выбора функции 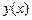при условии .

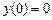Как видим, в отличие от предыдущих задач, правый конец искомой кривой заранее не определен: он может оказаться на любой точке вертикальной прямой 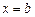. Мы приходим, таким образом, к задаче со свободной (подвижной) границей. Найдем ее решение в общей постановке.

Вариационная задача с вертикальными границами

Пусть в задаче об отыскании экстремума функционала

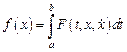
фиксирована одна граничная точка 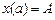, условий же на 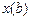нет. Иными словами, второй конец допустимой кривой может перемещаться по вертикальной прямой .

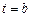Нулевая вариация 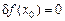, как и ранее, является необходимым условием экстремальности. Вычисляя вариацию функционала по известной формуле, получаем:

.

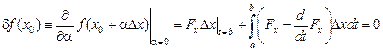Как и ранее, 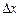– произвольная функция, в частности, можно взять 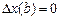, что сведет задачу к уже решенной задаче с закрепленными границами. Для нее, как известно, необходимое условие экстремальности означает обращение в тождество уравнения Эйлера. Отсюда следует, что 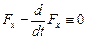, то есть интеграл в формуле для вариации равен нулю.

Теперь выберем функцию 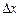так, чтобы 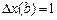. Тогда требование равенства нулю вариации сводится к условию

.

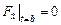Если бы левый конец тоже был свободным, получили бы аналогичное условие

.

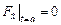Решение задачи навигации

Вернемся к задаче навигации и найдем ее решение, используя полученный выше результат.

Итак, нам следует найти минимум функционала

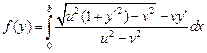
при условии 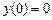, а 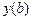может принимать любое значение.

Согласно вышеприведенной схеме, решаем уравнение Эйлера. Так как подынтегральная функция

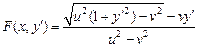
зависит только от 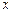и 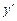, то уравнение Эйлера допускает первый интеграл: 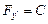. С другой стороны, поскольку вторая граница экстремали перемещается по вертикальной прямой, для нее должно выполняться условие 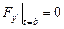. Отсюда сразу следует, что вышеприведенный первый интеграл имеет вид: 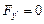. Получаем дифференциальное уравнение первого порядка

,

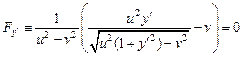для которого легко найти решение. Находя явное выражение для 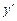, получаем 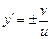. Так как предполагается (см. рис. 1), что переправа осуществляется с левого берега на правый, то перед дробью следует выбрать знак плюс. Учитывая, что 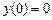, получаем окончательно:

.

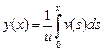В частности, если 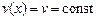, то искомый маршрут наибыстрейшей переправы реализуется на прямой .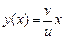