Линейные дифференциальные уравнения
Второго порядка и свойства их решений
Многие задачи физики, механики и техники приводят к дифференциальным уравнениям в частных производных второго порядка, причем линейных относительно искомой функции и ее частных производных.
Общий вид линейного дифференциального уравнения второго порядка при условии, что функция 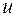 зависит от двух переменных
зависит от двух переменных 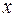 и
и 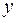 , таков:
, таков:
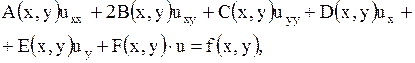 | (1.88) |
где 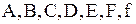 - данные непрерывные функции, определяемые в некоторой области
- данные непрерывные функции, определяемые в некоторой области 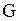 переменных
переменных 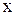 и
и 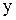 , причем
, причем 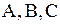 имеют непрерывные частные производные до 2-го порядка включительно.
имеют непрерывные частные производные до 2-го порядка включительно.
Чаще всего коэффициенты перед искомой функцией 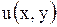 и ее производными – числа.
и ее производными – числа.
Если в уравнении (1.88) 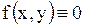 , то уравнение называется однородным; если
, то уравнение называется однородным; если 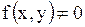 , то уравнение называется неоднородным.
, то уравнение называется неоднородным.
Обсудим особенность решений однородного уравнения
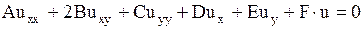 . . | (1.89) |
Решения линейных однородных уравнений вида (1.89) обладают следующим свойством.
Если каждая из функций 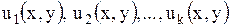 является решением уравнения (1.89), то и их линейная комбинация
является решением уравнения (1.89), то и их линейная комбинация
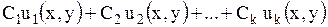 , , | (1.90) |
где 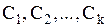 - произвольные постоянные, также является решением этого уравнения.
- произвольные постоянные, также является решением этого уравнения.
Это утверждение легко проверить, подставив в уравнение (1.89) вместо 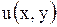 выражение (1.90) и производные
выражение (1.90) и производные 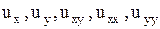 указанной линейной комбинации.
указанной линейной комбинации.
Такое же свойство, как известно, имеет место для обыкновенных дифференциальных уравнений, но 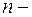 го порядка.
го порядка.
Уравнение же в частных производных может иметь бесконечное множество линейно независимых частных решений, т.е. такое множество решений, любое конечное число которых является функциями линейно независимыми. (Напомним, система функций 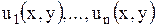 называется линейно независимой, если ни одна из этих функций не является линейной комбинацией остальных). В соответствии с этим имеют дело с рядами, членами которых служат произведения произвольных постоянных на частные решения:
называется линейно независимой, если ни одна из этих функций не является линейной комбинацией остальных). В соответствии с этим имеют дело с рядами, членами которых служат произведения произвольных постоянных на частные решения:
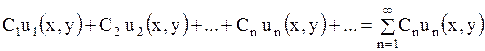 . . | (1.91) |
Будем рассматривать только такие ряды, суммы которых есть непрерывные функции
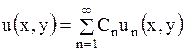 .
.
Кроме того, будем предполагать, что эти ряды можно дважды почленно дифференцировать. При таких предположениях функция 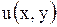 , которая есть сумма ряда (1.91), так же как и члены ряда, является решением уравнения (1.89).
, которая есть сумма ряда (1.91), так же как и члены ряда, является решением уравнения (1.89).
Классификация линейных уравнений и приведение
Их к каноническому виду
Линейные уравнения второго порядка в частных производных делят на три класса, в каждом из которых есть простейшие уравнения, называемые каноническими. Решения уравнений одного и того же класса имеют много общих свойств. Для изучения этих свойств достаточно рассмотреть канонические уравнения, так как другие уравнения данного типа могут быть приведены к каноническому виду.
Запишем линейное относительно производных второго порядка уравнение (1.88) в более краткой форме:
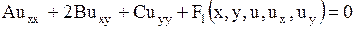 . . | (1.92) |
Классификация уравнений вида (1.92) проводится в соответствии со знаком дискриминанта 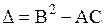 .
.
Если в некоторой области 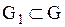 выражение
выражение 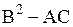 сохраняет знак, то уравнение (1.92) в этой области принадлежит:
сохраняет знак, то уравнение (1.92) в этой области принадлежит:
а) к гиперболическому типу, если 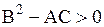 ;
;
б) параболическому типу, если 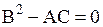 ;
;
в) эллиптическому типу, если 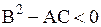 .
.
Пример. Определить тип уравнения
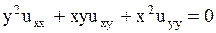 .
.
Решение. Здесь 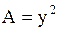 ,
, 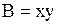 ,
, 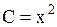 и
и 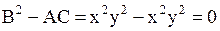 для любых
для любых 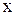 и
и 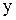 . Значит, на всей плоскости, а следовательно и в некоторой области задания, данное уравнение является уравнением параболического типа.
. Значит, на всей плоскости, а следовательно и в некоторой области задания, данное уравнение является уравнением параболического типа.
Если уравнение рассматривается в области задания 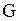 , то указанные три типа не всегда дают исчерпывающую классификацию, так как выражение
, то указанные три типа не всегда дают исчерпывающую классификацию, так как выражение 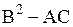 может не сохранять знак во всей области. Тогда должна существовать кривая
может не сохранять знак во всей области. Тогда должна существовать кривая 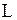 , вдоль которой выражение
, вдоль которой выражение 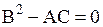 ; эта кривая называется линией параболического вырождения. При этом возможны два случая:
; эта кривая называется линией параболического вырождения. При этом возможны два случая:
1) во всех точках 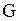 , кроме
, кроме 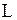 ,
, 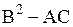 сохраняет знак, тогда уравнение (1.92) называется уравнением гиперболического или эллиптического типа с линией вырождения
сохраняет знак, тогда уравнение (1.92) называется уравнением гиперболического или эллиптического типа с линией вырождения 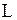 ;
;
2) выражение 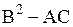 меняет знак в области
меняет знак в области  , тогда уравнение (1.92) называется уравнением смешанного типа.
, тогда уравнение (1.92) называется уравнением смешанного типа.
Пример. Определить тип уравнения
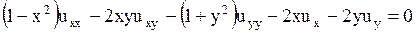 .
.
Решение. Здесь 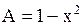 ,
, 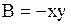 ,
, 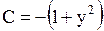 и, следовательно,
и, следовательно, 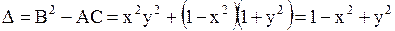 . Дискриминант
. Дискриминант 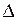 равен нулю, когда
равен нулю, когда 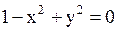 . Значит, гипербола
. Значит, гипербола 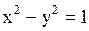 является линией параболического вырождения, а данное уравнение относится к смешанному типу, причем области
является линией параболического вырождения, а данное уравнение относится к смешанному типу, причем области 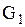 , где
, где 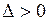
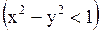 , и
, и 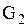 , где
, где 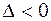
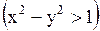 , являются областями гиперболичности и эллиптичности.
, являются областями гиперболичности и эллиптичности.
Уравнение вида
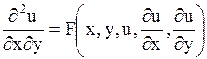 | (1.93) |
называется каноническим уравнением гиперболического типа.
Второй канонический вид уравнения гиперболического типа таков:
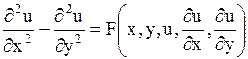 . . | (1.94) |
Уравнение вида
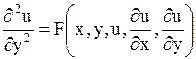 | (1.95) |
называется каноническим уравнением параболического типа.
Уравнение вида
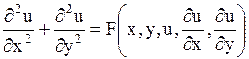 | (1.96) |
называется каноническим уравнением эллиптического типа.
Уравнение (1.92) в каждой из областей, где сохраняется знак дискриминанта 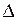 , может быть приведено к уравнению, эквивалентному данному, а именно к каноническому, путем введения вместо
, может быть приведено к уравнению, эквивалентному данному, а именно к каноническому, путем введения вместо 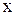 и
и 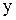 новых переменных
новых переменных 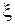 и
и 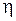 с помощью зависимостей
с помощью зависимостей
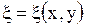 , , 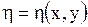 . . | (1.97) |
При этом от функций 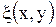 ,
, 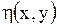 требуется, чтобы они были дважды непрерывно дифференцируемыми и чтобы якобиан
требуется, чтобы они были дважды непрерывно дифференцируемыми и чтобы якобиан 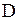 , т.е. функциональный определитель
, т.е. функциональный определитель
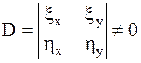
в рассматриваемой области  . Выражая производные, входящие в уравнение (1.92), по старым переменным через производные по новым переменным, приходят к уравнению
. Выражая производные, входящие в уравнение (1.92), по старым переменным через производные по новым переменным, приходят к уравнению
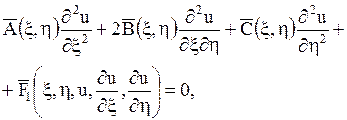 | (1.98) |
где
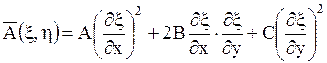 ,
,
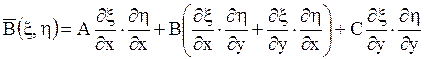 ,
,
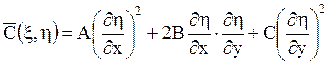 .
.
Непосредственной подстановкой нетрудно проверить, что
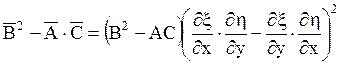 .
.
Из последнего соотношения следует инвариантность типа уравнения при преобразовании переменных, если только якобиан 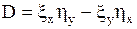 отличен от нуля.
отличен от нуля.
В преобразовании (1.97) две функции 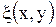 и
и 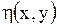 можно выбрать так, чтобы выполнялось только одно из условий: 1)
можно выбрать так, чтобы выполнялось только одно из условий: 1) 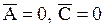 ,
,
2) 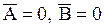 , 3)
, 3) 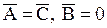 . Другими словами, функции
. Другими словами, функции 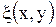 и
и 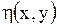 подбираются такими, чтобы в уравнении гиперболического типа исчезли члены с производными
подбираются такими, чтобы в уравнении гиперболического типа исчезли члены с производными 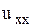 ,
, 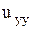 , в уравнении параболического типа исчезли члены с производными
, в уравнении параболического типа исчезли члены с производными 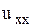 ,
, 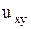 , в уравнении эллиптического типа -
, в уравнении эллиптического типа - 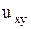 . Тогда, очевидно, преобразованное уравнение (1.98) примет наиболее простой вид – канонический.
. Тогда, очевидно, преобразованное уравнение (1.98) примет наиболее простой вид – канонический.
Обоснование процедуры канонизации уравнения вида (1.92) мы не приводим; читатель может познакомиться с ним в книгах /1,3/. Здесь же излагается формальная сторона этой процедуры.
Для приведения уравнения (1.92) к каноническому виду надо составить вспомогательное обыкновенное дифференциальное уравнение
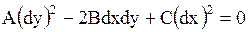 , , | (1.99) |
которое называется характеристическим для данного уравнения (1.92).
Характеристическое уравнение (1.99) распадается на два уравнения:
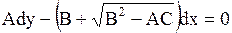 (или (или 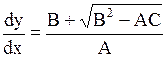 ), ), | (1.100) |
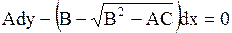 (или (или 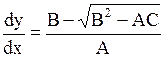 ). ). | (1.101) |
Общие интегралы уравнений (1.100) и (1.101)
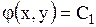 и
и 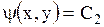
называют характеристиками данного уравнения (1.92) или характеристическими кривыми. (В связи с этим рассматриваемый метод упрощения уравнения (1.92) называют методом характеристик).
Через каждую точку области 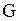 , где уравнение имеет один и тот же тип, проходят две характеристики, причем для уравнений гиперболического типа характеристики действительны и различны, для уравнений эллиптического типа – комплексны и различны, а для уравнений параболического типа обе характеристики действительны и совпадают.
, где уравнение имеет один и тот же тип, проходят две характеристики, причем для уравнений гиперболического типа характеристики действительны и различны, для уравнений эллиптического типа – комплексны и различны, а для уравнений параболического типа обе характеристики действительны и совпадают.
Разберем каждый из этих случаев в отдельности.
СЛУЧАЙ 1. Для уравнений гиперболического типа 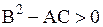 и правые части уравнений (1.100) и (1.101) действительны и различны. Общие интегралы их
и правые части уравнений (1.100) и (1.101) действительны и различны. Общие интегралы их 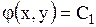 и
и 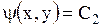 определяют два различных семейства действительных кривых – характеристик уравнения (1.92).
определяют два различных семейства действительных кривых – характеристик уравнения (1.92).
В этом случае, как установлено, для приведения уравнения (1.92) к каноническому виду следует сделать замену переменных, положив
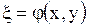 ,
, 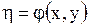 ,
,
в результате чего исходное уравнение преобразуется в уравнение вида
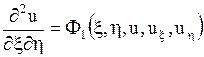 .
.
Таким образом, получается каноническая форма уравнения гиперболического типа.
Отметим, что с помощью дополнительной замены ( 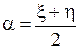 ,
, 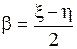 , где
, где 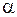 и
и 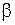 - новые переменные) уравнение (1.92) может быть приведено к другой канонической форме:
- новые переменные) уравнение (1.92) может быть приведено к другой канонической форме:
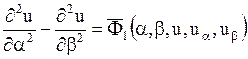 .
.
СЛУЧАЙ 2. Для уравнений параболического типа 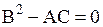 , поэтому уравнения (1.100), (1.101) совпадают и результатом их решения является один действительный интеграл
, поэтому уравнения (1.100), (1.101) совпадают и результатом их решения является один действительный интеграл 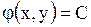 .
.
В этом случае для приведения уравнения (1.92) к каноническому виду в качестве одной из переменной, например, 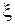 , берут
, берут
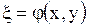 ,
,
другая же переменная выбирается произвольно:
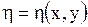
(например, 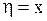 ), лишь бы только якобиан
), лишь бы только якобиан
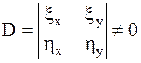 .
.
При таком выборе новых переменных 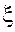 и
и 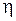 уравнение (1.92) принимает канонический вид:
уравнение (1.92) принимает канонический вид:
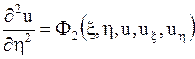 .
.
СЛУЧАЙ 3. Для уравнений эллиптического типа 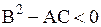 . В этом случае правые части уравнений (1.100) и (1.101) комплексны, а интегралы их будут комплексно-сопряженные. Они определяют два семейства мнимых характеристик.
. В этом случае правые части уравнений (1.100) и (1.101) комплексны, а интегралы их будут комплексно-сопряженные. Они определяют два семейства мнимых характеристик.
Пусть общий интеграл уравнения (1.100) имеет вид
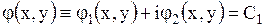 ,
,
где 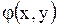 - функция, принимающая комплексные значения, а функции
- функция, принимающая комплексные значения, а функции 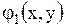 и
и 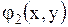 - действительные функции действительных переменных. Другой общий интеграл (уравнения (1.101) будет комплексно - сопряженным с указанным.
- действительные функции действительных переменных. Другой общий интеграл (уравнения (1.101) будет комплексно - сопряженным с указанным.
Если положить
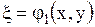 ,
, 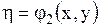 ,
,
то уравнение (1.92) принимает канонический вид:
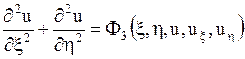 .
.
Примечание. После выбора новых переменных 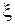 и
и 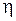 требуется преобразовать производные, входящие в данное уравнение, к новым переменным. Напомним, что первые производные по старым переменным
требуется преобразовать производные, входящие в данное уравнение, к новым переменным. Напомним, что первые производные по старым переменным 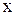 и
и 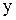 выражаются через производные по новым переменным
выражаются через производные по новым переменным 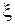 и
и 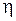 по известным формулам дифференцирования сложной функции:
по известным формулам дифференцирования сложной функции:
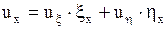 ,
, 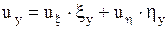 .
.
Вторые производные находятся путем дифференцирования выражений для 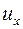 и
и 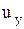 , так как
, так как
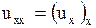 ,
, 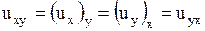 ,
, 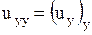 ;
;
при этом при отыскании 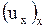 ,
, 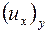 ,
, 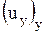 опять применяется правило дифференцирования сложной функции.
опять применяется правило дифференцирования сложной функции.
Пример. Привести к каноническому виду уравнение
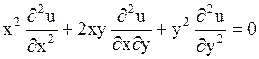 .
.
Решение. Здесь 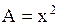 ,
, 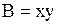 ,
, 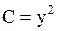 и
и 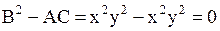 . Значит данное уравнение является уравнением параболического типа всюду.
. Значит данное уравнение является уравнением параболического типа всюду.
Составим характеристическое уравнение
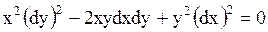 ,
,
которое можно записать в виде
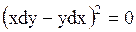 ,
,
откуда получаем
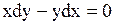 .
.
Разделяя переменные в этом уравнении 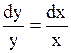 , после интегрирования его найдем
, после интегрирования его найдем
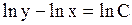 или
или 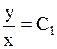 .
.
В соответствии с рассмотренным случаем 2 делаем замену переменных следующим образом:
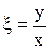 ,
, 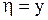 .
.
Так как функция 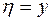 выбиралась произвольно, то надо проверить выполнимость условия
выбиралась произвольно, то надо проверить выполнимость условия
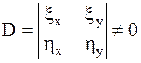 .
.
Найдем 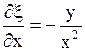 ,
, 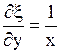 ,
, 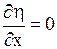 ,
, 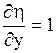 .
.
Тогда
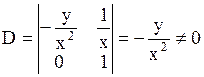 .
.
Выразим 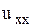 ,
, 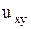 ,
, 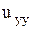 через новые переменные
через новые переменные 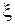 и
и  .
.
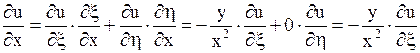 ;
;
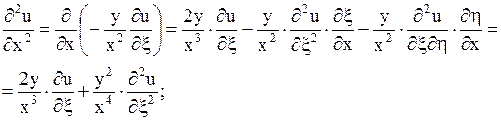
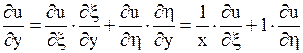 ;
;
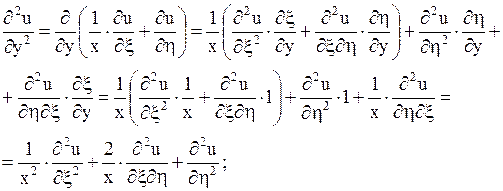
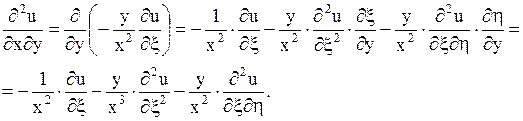
Значения 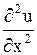 ,
, 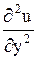 ,
, 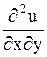 подставим в данное уравнение:
подставим в данное уравнение:
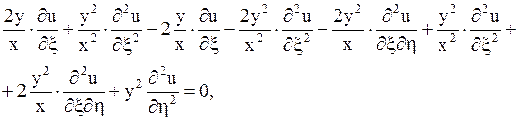
откуда получаем
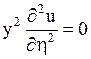 или
или 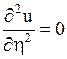 .
.
