Идеальные усилители напряжения и тока
Идеальным усилителем напряжения называется активный невзаимный четырехполюсник, напряжение на выходе которого в любой момент времени прямо пропорционально напряжению на входе, а входной ток равен нулю:
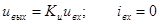 . (5.31)
. (5.31)
Коэффициент пропорциональности между входным и выходным напряжениями 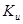 представляет собой вещественное число, называемое коэффициентом усиления по напряжению.
представляет собой вещественное число, называемое коэффициентом усиления по напряжению.
При 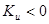 напряжения на входе и выходе имеют разные знаки (при гармоническом внешнем воздействии напряжения
напряжения на входе и выходе имеют разные знаки (при гармоническом внешнем воздействии напряжения 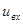 и
и 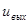 находятся в противофазе). Усилитель напряжения такого типа называется инвертирующим.
находятся в противофазе). Усилитель напряжения такого типа называется инвертирующим.
При 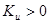 напряжения на входе и выходе усилителя имеют одинаковые знаки (совпадают по фазе). Такой усилитель называется неинвертирующим.
напряжения на входе и выходе усилителя имеют одинаковые знаки (совпадают по фазе). Такой усилитель называется неинвертирующим.
При 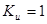 напряжение на выходе усилителя равно напряжению на его входе. Усилитель такого типа называется идеальным повторителем напряжения.
напряжение на выходе усилителя равно напряжению на его входе. Усилитель такого типа называется идеальным повторителем напряжения.
Схема замещения идеального усилителя напряжения может быть представлена в виде ИНУН с вещественным коэффициентом управления 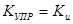 . Очевидно, что входное сопротивление идеального усилителя напряжения бесконечно велико, а выходное сопротивление равно нулю.
. Очевидно, что входное сопротивление идеального усилителя напряжения бесконечно велико, а выходное сопротивление равно нулю.
Идеальным усилителем тока называется активный невзаимный четырехполюсник, ток на выходе которого в любой момент времени пропорционален входному току, а напряжение на входе равно нулю:
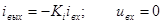 . (5.32)
. (5.32)
Коэффициент пропорциональности 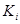 между входным и выходным токами представляет собой вещественное число и называется коэффициентом усиления по току. Схема замещения идеального усилителя тока содержит ИТУТ с вещественным коэффициентом управления
между входным и выходным токами представляет собой вещественное число и называется коэффициентом усиления по току. Схема замещения идеального усилителя тока содержит ИТУТ с вещественным коэффициентом управления 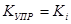 . Входное сопротивление идеального усилителя тока равно нулю, а выходное сопротивление бесконечно велико.
. Входное сопротивление идеального усилителя тока равно нулю, а выходное сопротивление бесконечно велико.
Из анализа основных уравнений (5.31) и (5.32) следует, что коэффициент усиления по току идеального усилителя напряжения и коэффициент усиления по напряжению идеального усилителя тока бесконечно велики и, следовательно, коэффициенты усиления по мощности обоих усилителе равны бесконечности.
| Наиболее широкое применение в теории цепей нашли идеальные усилители напряжения, условное графическое изображение которых приведено на рис. 5.18. Бесконечно большое входное и нулевое выходное сопротивления идеального | 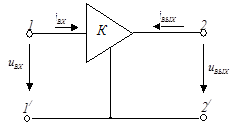 |
| Рис. 5.18 |
усилителя напряжения позволяют применять его для усиления в заданное число раз напряжения и одновременного «развязывания», т. е. электрического разделения источника энергии и нагрузки.
Идеальные операционные усилители
Идеальными операционным усилителем (ОУ) называется идеальный усилитель напряжения с бесконечно большим коэффициентом усиления. Идеальный ОУ представляет собой упрощенную модель широкого класса реальных устройств – операционных усилителей, выпускаемых в виде интегральных полупроводниковых микросхем. Первоначально усилители такого типа использовались в аналоговой вычислительной технике для моделирования различных математических операций (умножения, сложения, интегрирования и т. п.), чем и объясняется происхождение термина «операционный усилитель».
Наибольшее распространение получили ОУ с двумя входными зажимами (ОУ с дифференциальным входом), напряжение на выходе которых пропорционально разности напряжений на входных зажимах:
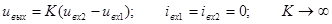 . (5.33)
. (5.33)
Схема замещения идеального ОУ с дифференциальным входом и его условное графическое обозначение приведены на рис. 5.19 а, б. Условное графическое изображение реального ОУ в соответствии с ГОСТ 2.759 – 82 приведено на рис. 5.19 в.
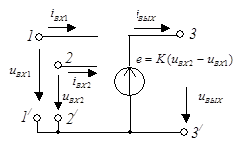 | 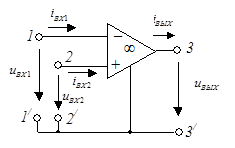 | 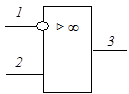 |
| а | б | в |
| Рис. 5.19 |
Как следует из выражений (5.33) и рис. 5.19 а, при закорачивании зажимов 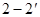 ОУ ведет себя как инвертирующий, а при закорачивании зажимов
ОУ ведет себя как инвертирующий, а при закорачивании зажимов 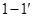 как неинвертирующий усилитель напряжения с бесконечно большим коэффициентом усиления. Зажимы
как неинвертирующий усилитель напряжения с бесконечно большим коэффициентом усиления. Зажимы 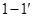 называются инвертирующими, а зажимы
называются инвертирующими, а зажимы 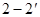 – неинвертирующими входами. На условном графическом изображении идеального ОУ (рис. 5.19 б) инвертирующий вход обозначен знаком «–», а неинвертирующий – «+». Следует помнить, что знаки «–» и «+» позволяют в данном случае только условно обозначить инвертирующий и неинвертирующий входы и не указывают на полярность подаваемых на них напряжений. Инвертирующий вход реального ОУ (рис. 5.19 в) обозначается кружком.
– неинвертирующими входами. На условном графическом изображении идеального ОУ (рис. 5.19 б) инвертирующий вход обозначен знаком «–», а неинвертирующий – «+». Следует помнить, что знаки «–» и «+» позволяют в данном случае только условно обозначить инвертирующий и неинвертирующий входы и не указывают на полярность подаваемых на них напряжений. Инвертирующий вход реального ОУ (рис. 5.19 в) обозначается кружком.
Анализ цепей с ОУ можно выполнять двумя способами, равноценными в смысле получаемых результатов:
1) заменяя ОУ схемой замещения (рис. 5.19 а) и составляя уравнения электрического равновесия полученной идеализированной цепи при 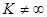 . После решения этих уравнений относительно интересующих токов и напряжений находятся пределы, к которым стремятся значения соответствующих величин при
. После решения этих уравнений относительно интересующих токов и напряжений находятся пределы, к которым стремятся значения соответствующих величин при 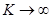 ;
;
2) не прибегая к схеме замещения ОУ, но учитывая, что при конечном выходном напряжении 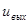 и бесконечно большом коэффициенте усиления
и бесконечно большом коэффициенте усиления 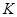 разность
разность 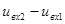 должна стремиться к нулю, т. е. зажимы 1 и 2 должны иметь одинаковый потенциал. Это допущение, а также учет того, что входные токи ОУ равны нулю, позволяет существенно упростить анализ цепей с ОУ.
должна стремиться к нулю, т. е. зажимы 1 и 2 должны иметь одинаковый потенциал. Это допущение, а также учет того, что входные токи ОУ равны нулю, позволяет существенно упростить анализ цепей с ОУ.
Идеальные преобразователи сопротивления
Преобразователями сопротивления называются четырехполюсники, входное сопротивление которых пропорционально сопротивлению или проводимости нагрузки. Различают два основных типа преобразователей сопротивления: конверторы и инверторы.
Идеальный конвертор сопротивления – это четырехполюсник, комплексное входное сопротивление которого пропорционально комплексному сопротивлению нагрузки:
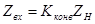 , (5.34)
, (5.34)
где 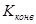 – вещественное число, называемое коэффициентом конверсии. При
– вещественное число, называемое коэффициентом конверсии. При 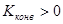 конвертор осуществляет преобразование сопротивления без изменения его знака. Конверторы такого типа называются конверторами положительного сопротивления или масштабными преобразователями сопротивления. К конверторам положительного сопротивления относится, в частности, идеальный трансформатор, коэффициент конверсии которого:
конвертор осуществляет преобразование сопротивления без изменения его знака. Конверторы такого типа называются конверторами положительного сопротивления или масштабными преобразователями сопротивления. К конверторам положительного сопротивления относится, в частности, идеальный трансформатор, коэффициент конверсии которого: 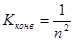 , где
, где 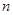 – коэффициент трансформации трансформатора.
– коэффициент трансформации трансформатора.
При 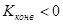 конвертор осуществляет преобразование сопротивления с изменением его знака. Конверторы такого типа получили название конверторов отрицательного сопротивления.
конвертор осуществляет преобразование сопротивления с изменением его знака. Конверторы такого типа получили название конверторов отрицательного сопротивления.
Сравнивая выражение (5.34) с соотношением (5.21) для входного сопротивления произвольного четырехполюсника нагруженного со стороны зажимов 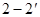 (рис. 5.12), определяем зависимость между
(рис. 5.12), определяем зависимость между 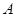 –параметрами идеального конвертора сопротивления:
–параметрами идеального конвертора сопротивления:
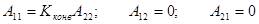 . (5.35)
. (5.35)
Очевидно, что у конверторов положительного сопротивления параметры 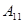 и
и 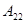 имеют одинаковые знаки, а у конверторов отрицательного сопротивления – противоположные.
имеют одинаковые знаки, а у конверторов отрицательного сопротивления – противоположные.
Используя соотношение (5.35), находим определитель матрицы 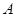 –параметров идеального конвертора сопротивлений:
–параметров идеального конвертора сопротивлений:
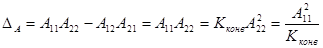 . (5.36)
. (5.36)
Следовательно, идеальный конвертор сопротивления является взаимным четырехполюсником при 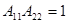 и невзаимным при
и невзаимным при 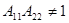 .
.
Подключая нагрузку 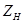 к зажимам
к зажимам 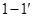 и учитывая выражения (5.22) и (5.35), определяем выходное сопротивление конвертора:
и учитывая выражения (5.22) и (5.35), определяем выходное сопротивление конвертора:
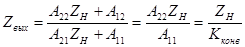 . (5.37)
. (5.37)
Как следует из выражения (5.37), характер преобразования сопротивления не изменится, если входные и выходные зажимы идеального конвертора сопротивления поменять местами, при этом коэффициент конверсии 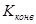 заменится обратной ему величиной
заменится обратной ему величиной 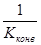 .
.
Если у конвертора сопротивления 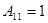 и, следовательно,
и, следовательно, 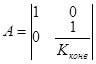 , то такой конвертор называется идеальным конвертором с преобразованием тока. Напряжение на выходе такого конвертора равно напряжению на входе, а токи отличаются в
, то такой конвертор называется идеальным конвертором с преобразованием тока. Напряжение на выходе такого конвертора равно напряжению на входе, а токи отличаются в 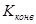 раз:
раз: 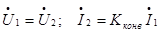 .
.
Если у конвертора сопротивления 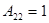 и, следовательно,
и, следовательно, 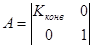 , то такой конвертор называют идеальным конвертором с преобразованием напряжения. Напряжения на входе и выходе такого конвертора отличаются в
, то такой конвертор называют идеальным конвертором с преобразованием напряжения. Напряжения на входе и выходе такого конвертора отличаются в 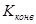 раз, а токи имеют одинаковые значения:
раз, а токи имеют одинаковые значения: 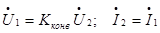 .
.
Идеальным инвертором сопротивления называется четырехполюсник, комплексное входное сопротивление которого пропорционально комплексной проводимости нагрузки:
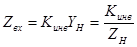 , (5.38)
, (5.38)
где 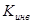 – вещественное число, называемое коэффициентом инверсии.
– вещественное число, называемое коэффициентом инверсии.
Сравнивая выражения (5.21) и (5.38), находим соотношения между 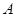 -параметрами идеального инвертора сопротивления:
-параметрами идеального инвертора сопротивления:
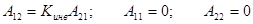 . (5.39)
. (5.39)
Нетрудно убедиться, что входное сопротивление инвертора не изменится, если его входные и выходные зажимы поменять местами:
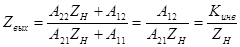 .
.
Определитель матрицы 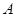 -параметров идеального инвертора сопротивления
-параметров идеального инвертора сопротивления
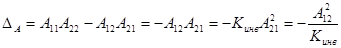 . (5.40)
. (5.40)
Следовательно, идеальный инвертор сопротивления является взаимным четырехполюсником только в случае 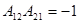 . При
. При 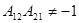 идеальный инвертор сопротивления является невзаимным четырехполюсником.
идеальный инвертор сопротивления является невзаимным четырехполюсником.
В зависимости от знака коэффициента инверсии различают инверторы положительного ( 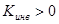 ) и отрицательного ( ) и отрицательного ( 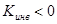 ) сопротивления. Частным случаем инвертора положительного сопротивления является идеальный гиратор, образованный двумя идеальными ИТУН (рис. 5.20). ) сопротивления. Частным случаем инвертора положительного сопротивления является идеальный гиратор, образованный двумя идеальными ИТУН (рис. 5.20). | 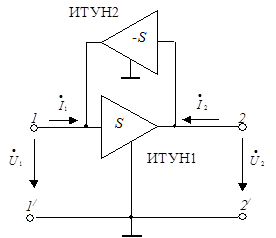 |
| Рис. 5.20 |
Единственным в данном случае параметром такого ИТУН служит крутизна 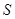 – вещественное число, называемое еще коэффициентом гирации или гираторной проводимостью. ИТУН2 отличается от ИТУН1 тем, что инвертирует, т. е. изменяет на противоположный знак выходного колебания.
– вещественное число, называемое еще коэффициентом гирации или гираторной проводимостью. ИТУН2 отличается от ИТУН1 тем, что инвертирует, т. е. изменяет на противоположный знак выходного колебания.
ИТУН1 создает на зажимах 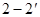 ток
ток 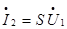 , в то время как ток на зажимах
, в то время как ток на зажимах 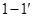 , создаваемый ИТУН2, определяется выходным напряжением:
, создаваемый ИТУН2, определяется выходным напряжением: 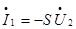 . Таким образом,
. Таким образом, 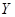 -матрица гиратора имеет вид
-матрица гиратора имеет вид 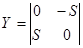 . Поскольку
. Поскольку 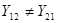 , то гиратор невзаимен. Пусть к зажимам
, то гиратор невзаимен. Пусть к зажимам 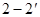 гиратора подключена нагрузка
гиратора подключена нагрузка 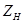 , т.е.
, т.е. 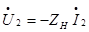 . Это означает, что
. Это означает, что 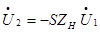 ; при этом на входе возникает ток с комплексной амплитудой
; при этом на входе возникает ток с комплексной амплитудой 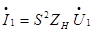 . Тогда входное сопротивление гиратора
. Тогда входное сопротивление гиратора
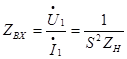 . (5.41)
. (5.41)
Примечательно, что если нагрузка носит ёмкостный характер 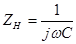 , то входное сопротивление гиратора имеет индуктивный характер
, то входное сопротивление гиратора имеет индуктивный характер 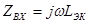 , где
, где 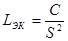 – эквивалентная индуктивность.
– эквивалентная индуктивность.
Гираторы обычно реализуются на базе интегральных схем операционных усилителей и используются для имитации индуктивных элементов в микроэлектронных цепях. При этом удается реализовать весьма большие номиналы индуктивностей. Так, при 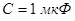 и
и 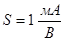 имеем
имеем 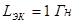 . Соответствующая катушка имела бы неприемлемо большие массу и габариты.
. Соответствующая катушка имела бы неприемлемо большие массу и габариты.
Если оба ИТУН одинаковы (рис. 5.21), то гиратор превращается в конвертор сопротивления, так как его входное сопротивление 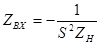 (5.42) Подключив к конвертору резистивную нагрузку (5.42) Подключив к конвертору резистивную нагрузку 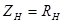 , получаем элемент с отрицательным входным , получаем элемент с отрицательным входным | 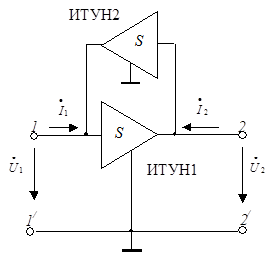 |
| Рис. 5.21 |
сопротивлением, который может использоваться, например, в автоколебательных устройствах.
Учебное издание
Ланских Анна Михайловна
ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА
Учебное пособие
Часть1. Основы электротехники
Подписано к использованию 18.12.13. Заказ № 1245.
Федеральное государственное бюджетное образовательное учреждение высшего
профессионального образования«Вятский государственный университет»
610000, Киров, ул. Московская, 36 Тел.: (8332) 64–23–56, http://vyatsu.ru
