Основные задачи теории систем.

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ СИСТЕМ

Определение понятия "система". В настоящее время нет единства в определении понятия "система". В первых определениях в той или иной форме говорилось о том, что система - это элементы и связи (отношения) между ними. Например, основоположник теории систем Людвиг фон Берталанфи определял систему как комплекс взаимодействующих элементов или как совокупность элементов, находящихся в определенных отношениях друг с другом и со средой. А. Холл определяет систему как множество предметов вместе со связями между предметами и между их признаками. Ведутся дискуссии, какой термин - "отношение" или "связь" - лучше употреблять.

Позднее в определениях системы появляется понятие цели. Так, в "Философском словаре" система определяется как "совокупность элементов, находящихся в отношениях и связях между собой определенным образом и образующих некоторое целостное единство".

В последнее время в определение понятия системы наряду с элементами, связями и их свойствами и целями начинают включать наблюдателя, хотя впервые на необходимость учета взаимодействия между исследователем и изучаемой системой указал один из основоположников кибернетики У. Р. Эшби.

М. Масарович и Я. Такахара в книге "Общая теория систем" считают, что система - "формальная взаимосвязь между наблюдаемыми признаками и свойствами".

Таким образом, в зависимости от количества учитываемых факторов и степени абстрактности определение понятия "система" можно представить в следующей символьной форме. Каждое определение обозначим буквой D (от лат. definitions) и порядковым номером, совпадающим с количеством учитываемых в определении факторов.

D1. Система есть нечто целое:

S=А(1,0).

Это определение выражает факт существования и целостность. Двоичное суждение А(1,0) отображает наличие или отсутствие этих качеств.

D2. Система есть организованное множество (Темников Ф. Е.):

S=(орг, М),

где орг - оператор организации; М - множество.

DЗ. Система есть множество вещей, свойств и отношений (Уемов А. И.):

S=({т},{n},{r}),

где т - вещи, n - свойства, r - отношения.

D4. Система есть множество элементов, образующих структуру и обеспечивающих определенное поведение в условиях окружающей среды:

S=(e, SТ, ВЕ, Е),

где e - элементы, SТ - структура, ВЕ - поведение, Е - среда.

D5. Система есть множество входов, множество выходов, множество состояний, характеризуемых оператором переходов и оператором выходов:

S=(Х, Y, Z, H, G),

где Х - входы, Y - выходы, Z - состояния, Н - оператор переходов, G - оператор выходов. Это определение учитывает все основные компоненты, рассматриваемые в автоматике.

D6. Это шестичленное определение, как и последующие, трудно сформулировать в словах. Оно соответствует уровню биосистем и учитывает генетическое (родовое) начало GN, условия существования КD, обменные явления МВ, развитие ЕV, функционирование FС и репродукцию (воспроизведения) RР:

S=(GN, KD, MB, EV, FC, RP).

D7. Это определение оперирует понятиями модели F, связи SС, пересчета R, самообучения FL, самоорганизации FQ, проводимости связей СО и возбуждения моделей JN:

S=(F, SС, R, FL, FO, СО, JN).

Данное определение удобно при нейрокибернетических исследованиях.

D8. Если определение D5 дополнить фактором времени и функциональными связями, то получим определение системы, которым обычно оперируют в теории автоматического управления:

S=(Т, X, Y, Z, W., V, h, j),

где Т - время, Х - входы, Y - выходы, Z - состояния, W. - класс операторов на выходе, V - значения операторов на выходе, h - функциональная связь в уравнении y(t₂)= h(x(t₁),z(t₁),t₂), j - функциональная связь в уравнении z(t₂)=j(x(t₁), z(t₁), t₂).

D9. Для организационных систем удобно в определении системы учитывать следующее:

S=(РL, RO, RJ, EX, PR, DT, SV, RD, EF),

где РL - цели и планы, RO - внешние ресурсы, RJ - внутренние ресурсы, ЕХ - исполнители, PR - процесс, DТ - помехи, SV - контроль, RD - управление, ЕF - эффект.

Последовательность определений можно продолжить до Dn (n=9, 10, 11, ...), в котором учитывалось бы такое количество элементов, связей и действий в реальной системе, которое необходимо для решаемой задачи, для достижения поставленной цели. В качестве "рабочего" определения понятия системы в литературе по теории систем часто рассматривается следующее: система - множество элементов, находящихся в отношениях и связях друг с другом, которое образует определенную целостность, единство.

Под системой, понимается объект свойства которого не сводятся без остатка к свойствам составляющих его дискретных элементов (неаддитив­ность свойств). Интегративное свойство системы обеспечивает ее целост­ность, качественно новое образование по сравнению с составляющими ее частями.

Любой элемент системы можно рассматривать как самостоятельную систему (математическую модель, описывающую какой - либо функциональный блок, или аспект изучаемой проблемы), как правило более низкого поряд­ка. Каждый элемент системы описывается своей функцией. Под функцией понимается присущее живой и костной материи вещественно-энергетические и информационные отношения между входными и выходными процессами. Если такой элемент обладает внутренней структурой, то его называют подсистемой, такое описание может быть ис­пользовано при реализации методов анализа и синтеза систем. Это нашло отражение в одном из принципов системного анализа - законе системнос­ти, говорящим о том что любой элемент может быть либо подсистемой в некоторой системе либо, подсистемой среди множества объектов аналогич­ной категории. Элемент всегда является частью системы и вне ее не представляет смысла.

Выбор определения системы.

Рассматривая различные определения системы и не выделяя ни одного из них в качестве основного обычно подчеркивают сложность понятия системы, неоднозначность выбора формы описания на различных стадиях исследования. При описании системы рекомендуется воспользоваться максимально полным способом, а потом выделить наиболее компоненты влияющие на ее функционирование и сформулировать рабочие описание системы.

Рассмотрим основные понятия, характеризующие строение и функционирование систем.

Элемент. Под элементом принято понимать простейшую неделимую часть системы. Ответ на вопрос, что является такой частью, может быть неоднозначным и зависит от цели рассмотрения объекта как системы, от точки зрения на него или от аспекта его изучения. Таким образом, элемент - это предел деления системы с точек зрения решения конкретной задачи и поставленной цели. Систему можно расчленить на элементы различными способами в зависимости от формулировки цели и ее уточнения в процессе исследования.

Подсистема. Система может быть разделена на элементы не сразу, а последовательным расчленением на подсистемы, которые представляют собой компоненты более крупные, чем элементы, и в то же время более детальные, чем система в целом. Возможность деления системы на подсистемы связана с вычленением совокупностей взаимосвязанных элементов, способных выполнять относительно независимые функции, подцели, направленные на достижение общей цели системы. Названием "подсистема" подчеркивается, что такая часть должна обладать свойствами системы (в частности, свойством целостности). Этим подсистема отличается от простой группы элементов, для которой не сформулирована подцель и не выполняются свойства целостности (для такой группы используется название "компоненты"). Например, подсистемы АСУ, подсистемы пассажирского транспорта крупного города.

Структура. Это понятие происходит от латинского слова structure, означающего строение, расположение, порядок. Структура отражает наиболее существенные взаимоотношения между элементами и их группами (компонентами, подсистемами), которые мало меняются при изменениях в системе и обеспечивают существование системы и ее основных свойств. Структура - это совокупность элементов и связей между ними. Структура может быть представлена графически, в виде теоретико-множественных описаний, матриц, графов и других языков моделирования структур.

Структуру часто представляют в виде иерархии. Иерархия - это упорядоченность компонентов по степени важности (многоступенчатость, служебная лестница). Между уровнями иерархической структуры могут существовать взаимоотношения строгого подчинения компонентов (узлов) нижележащего уровня одному из компонентов вышележащего уровня, т. е. отношения так называемого древовидного порядка. Такие иерархии называют сильными или иерархиями типа "дерева". Они имеют ряд особенностей, делающих их удобным средством представления систем управления. Однако могут быть связи и в пределах одного уровня иерархии. Один и тот же узел нижележащего уровня может быть одновременно подчинен нескольким узлам вышележащего уровня. Такие структуры называют иерархическими структурами «со слабыми связями». Между уровнями иерархической структуры могут существовать и более сложные взаимоотношения, например, типа "страт", "слоев", "эшелонов". Примеры иерархических структур: энергетические системы, АСУ, государственный аппарат.

Связь. Понятие "связь" входит в любое определение системы наряду с понятием "элемент" и обеспечивает возникновение и сохранение структуры и целостных свойств системы. Это понятие характеризует одновременно и строение (статику), и функционирование (динамику) системы.

Связь характеризуется направлением, силой и характером (или видом). По первым двум признакам связи можно разделить на направленные и ненаправленные, сильные и слабые, а по характеру - на связи подчинения, генетические, равноправные (или безразличные), связи управления. Связи можно разделить также по месту приложения (внутренние и внешние), по направленности процессов в системе в целом или в отдельных ее подсистемах (прямые и обратные). Связи в конкретных системах могут быть одновременно охарактеризованы несколькими из названных признаков.

Важную роль в системах играет понятие "обратной связи". Это понятие, легко иллюстрируемое на примерах технических устройств, не всегда можно применить в организационных системах. Исследованию этого понятия большое внимание уделяется в кибернетике, в которой изучается возможность перенесения механизмов обратной связи, характерных для объектов одной физической природы, на объекты другой природы. Обратная связь является основой саморегулирования и развития систем, приспособления их к изменяющимся условиям существования.

Состояние. Понятием "состояние" обычно характеризуют мгновенную фотографию, "срез" системы, остановку в ее развитии. Его определяют либо через входные воздействия и выходные сигналы (результаты), либо через макропараметры, макросвойства системы (например, давление, скорость, ускорение - для физических систем; производительность, себестоимость продукции, прибыль - для экономических систем).

Более полно состояние можно определить, если рассмотреть элементы e (или компоненты, функциональные блоки), определяющие состояние, учесть, что "входы" можно разделить на управляющие u и возмущающие х (неконтролируемые) и что "выходы" (выходные результаты, сигналы) зависят от e, u и х, т.е. z_t=f(e_t, u_t, x_t). Тогда в зависимости от задачи состояние может быть определено как {e, u}, {e, u, z} или {e, х, u, z}.

Таким образом, состояние - это множество существенных свойств, которыми система обладает в данный момент времени.

Поведение. Если система способна переходить из одного состояния в другое (например, z₁®z₂®z₃), то говорят, что она обладает поведением. Этим понятием пользуются, когда неизвестны закономерности переходов из одного состояния в другое. Тогда говорят, что система обладает каким-то поведением и выясняют его закономерности. С учетом введенных выше обозначений поведение можно представить как функцию z_t=f(z_t-1, x_t, u_t).

Внешняя среда. Под внешней средой понимается множество элементов, которые не входят в систему, но изменение их состояния вызывает изменение поведения системы.

Модель. Под моделью системы понимается описание системы, отображающее определенную группу ее свойств. Углубление описания - детализация модели. Создание модели системы позволяет предсказывать ее поведение в определенном диапазоне условий.

Модель функционирования (поведения) системы - это модель, предсказывающая изменение состояния системы во времени, например: натурные (аналоговые), электрические, машинные на ЭВМ и др.

Равновеcие - это способность системы в отсутствие внешних возмущающих воздействий (или при постоянных воздействиях) сохранить свое состояние сколь угодно долго.

Устойчивость. Под устойчивостью понимается способность системы возвращаться в состояние равновесия после того, как она была из этого состояния выведена под влиянием внешних возмущающих воздействий. Эта способность обычно присуща системам при постоянном и„ если только отклонения не превышают некоторого предела.

Состояние равновесия, в которое система способна возвращаться, по аналогии с техническими устройствами называют устойчивым состоянием равновесия. Равновесие и устойчивость в экономических и организационных системах - гораздо более сложные понятия, чем в технике, и до недавнего времени ими пользовались только для некоторого предварительного описательного представления о системе. В последнее время появились попытки формализованного отображения этих процессов и в сложных организационных системах, помогающие выявлять параметры, влияющие на их протекание и взаимосвязь.

Развитие. Исследованию процесса развития, соотношения процессов развития и устойчивости, изучению механизмов, лежащих в их основе, уделяют в кибернетике и теории систем большое внимание. Понятие развития помогает объяснить сложные термодинамические и информационные процессы в природе и обществе.

Цель. Применение понятия "цель" и связанных с ним понятий целенаправленности, целеустремленности, целесообразности сдерживается трудностью их однозначного толкования в конкретных условиях. Это связано с тем, что процесс целеобразования и соответствующий ему процесс обоснования целей в организационных системах весьма сложен и не до конца изучен. Его исследованию большое внимание уделяется в психологии, философии, кибернетике. В Большой Советской Энциклопедии цель определяется как "заранее мыслимый результат сознательной деятельности человека". В практических применениях цель - это идеальное устремление, которое позволяет коллективу увидеть перспективы или реальные возможности, обеспечивающие своевременность завершения очередного этапа на пути к идеальным устремлениям.

В настоящее время в связи с усилением программно-целевых принципов в планировании исследованию закономерностей целеобразования и представления целей в конкретных условиях уделяется все больше внимания. Например: энергетическая программа, продовольственная программа, жилищная программа, программа перехода к рыночной экономике. Понятие цель лежит в основе развития системы.

Основные понятия и определения

Основное содержание первой лекции

В первой лекции были рассмотрены понятия: система, элемент, подсистема структура и связь, иерархия состояние, поведение, внешняя среда.

Под системой, понимается объект свойства которого не сводятся без остатка к свойствам составляющих его дискретных элементов (неаддитивность свойств). Интегративное свойство системы обеспечивает ее целостность, качественно новое образование по сравнению с составляющими ее частями.

Любой элемент системы можно рассматривать как самостоятельную систему (математическую модель, описывающую какой - либо функциональный блок, или изучаемой аспект), как правило более низкого порядка. Каждый элемент системы описывается своей функцией. Под функцией понимается вещественно-энергетические и информационные отношения между входными и выходными процессами. Если такой элемент обладает внутренней структурой, то его называют подсистемой. Такое описание может быть использовано при реализации методов анализа и синтеза систем. Это нашло отражение в одном из принципов системного анализа - законе системности, говорящим о том что любой элемент может быть либо подсистемой в некоторой системе либо, подсистемой среди множества объектов аналогичной категории. Элемент всегда является частью системы и вне ее не представляет смысла. Под структурой понимается внутренняя форма, взаимодействие и связь элементов в рамках данной системы.

Входы и выходы- материальные или информационные потоки входящие и выходящие из системы.

Цель системы. Состояние системы описывается рядом переменных x₁..x_n. Одна из переменных или группа переменных x_i, должна поддерживаться в определенном значении x_i=F(X,t) (или диапазоне значений), называемой целевой функцией.

Понятие информации

Информация - совокупность сведений, воспринимаемых из окружающий среды, выдаваемых в окружающую среду либо сохраняемой внутри информационной системы.

Данные - представление в формальном виде конкретная информация об объектах предметной области, их свойствах и взаимосвязях, отражающая события и ситуации в этой области.

Данные представляются в виде позволяющим автоматизировать их сбор, хранение и дальнейшую обработку информационными системами. Данные это запись в соответствующем коде.

Информация в ЭВМ делится на:

n процедурную (выполняемые программы);

n декларативную (данные которые обрабатывают программы).

Организация хранения и обработки больших объемов информации привела к появлению баз данных.

На рис. представлена структура СУБД (стр.24)

Открытые и закрытые системы

Закрытые системы - нет поступление энергии (информации) из вне системы или выход энергии (информации) из системы во внешнюю среду.

Модель и цель системы

Понятие модели трактуется неоднозначно. В основе его лежит сходство процессов протекающих в реальной действительности и в заменяемым реальный объект модели. В философии, под моделью понимается широкая категория кибернетики, заменяющая изучаемый объект его упрощенным представлением, с целью более глубокого познания оригинала. Под математической моделью (в дальнейшим просто моделью) понима­ется идеальное математическое отражение исследуемого объекта.

Фундаментальные (детальные) модели, количественно описывающих поведение или свойства системы, начиная с такого числа основных физических допущений (первичных принципов), какое только является возможным. Такие модели предельно подробны и точны для явлений, которые они описывают.

Феноменологические модели используются для качественного описания физических процессов, когда точные соотношения неизвестны, либо слишком сложны для применения. Такие приближенные или осредненные модели обычно обоснованы физически и содержат входные данные, полученные из эксперимента или более фундаментальных теорий. Феноменологическая модель основывается на качественном понимании физической ситуации. При получении феноменологических моделей используются общие принципы и условия сохранения.

Управление

В широком смысле слова под управлением понимается организационную деятельность, осуществляющую функции и направленную на достижении определенных целей.

Структура системы управления.

Системы управления

Системы управления (СУ) представляют собой особый класс динамических систем, отличающихся наличием самостоятельных функций и целей управления и необходимым для реализации этих функций и целей высоким уровнем специальной системной организации .

Устройства связи и управления существенно отличаются от обычных технических устройств, тем что энергетические отношения в них не играют существенной роли, а основное внимание обращается на способность передавать и перерабатывать без искажений большое количество информации. Так в линии радиосвязи ничтожная доля энергии излучаемой антенной передатчика получатся антенной радиоприемника. КПД такого устройства, с точки зрения передачи энергии чрезвычайно мало, однако цель - передача информации выполняется.

Структуру процесса управления можно представить следующим образом.

Управление		ОУ		Состояние ОУ
Канал связи		УУ		Канал связи
Алгоритмы управления		Модель ОУ		Цель управления и критерий

Цель управления определяет состояние объекта которые должны быть достигнуты в процессе управления.

Разомкнутые системы управления

Системы управления с компенсацией возмущений

Системы управления с обратной связью

Реляционная модель данных

Реляционная модель данных характеризуется:

n информационной конструкцией;

n допустимыми операциями (выборкой, соединением и др.);

n ограничениями (функциональными зависимостями между атрибутами).

Реализационная база данных может быть описана как:

S(rel)=<A, R, Dom, Rel, V(s)>

где

A - множество имен переменных;

R - множество имен отношений;

Dom - вхождение атрибутов в домены;

Rel - вхождение атрибутов в отношения;

V(s) - множество ограничений.

Описание процесса обработки отношений может быть выполнено двумя способами:

n указанием перечня операций, выполнение которых приводит к требуемому результату (процедурный подход);

n описанием требуемых свойств (декларативный подход).

Множество операций и отношений образуют реляционную алгебру.

Как правило, список операций содержит проекцию, выборку, объединение, пересечение, вычитание, соединение и деление.

Проекцией называется операция, которая переносит результирующие отношения столбцы исходного отношения.

T=R[X].

R - исходное отношение;

T - результирующие отношение;

X - список атрибутов (условие проекции).

Выборка

Выборка - перенос в результирующие отношение строки удовлетворяющие условию выборки.

T=R[p].

R - исходное отношение;

T - результирующие отношение;

p - условие выборки.

Операция объединения, пересечения, вычитания.

Исходные отношения R1 и Р2, результирующие - T.

Операция объединения

Т=U(R1,R2)

Отношение Т содержит строки встречающиеся в отношениях R1 или в R2.

Операция пересечения

Т=I(R1,R2)

Отношение Т содержит строки встречающиеся одновременно в отношениях R1 и в R2.

Операция вычитания

Т=М(R1,R2)

Отношение Т содержит строки из отношения R1 за исключением строк встречающихся в отношении R2.

Операция соединения отношений.

T=R1 [p] R2

p - условие соединения.

Если строка из R1 по очереди сопоставляется со строками из R2 и если условие [p] выполняется, то строки сцепляются.

Операция натурального соединения

Операция не содержит условия

T=R1*R2

Если структуры R1 и R2 не содержат общих атрибутов то производится сцепление каждой строки из R1 со всеми строками из R2.

Основные свойства операции натурального соединения

Свойство коммутативности

R*S=S*R

Свойство ассоциативности

(R*S)*T=R*(S*T)

Виды информационных систем

Классификация ИС: по виду формализованного аппарата представления (детерминированные, стохастические); по сложности структуры и поведения; по степени организованности («хорошо» и «плохо» организованные, самоорганизующиеся).

Открытые и закрытые системы

Понятие открытой системы ввел Л. фон Берталанфи. Основные отличительные черты открытых систем - способность обмениваться с внешней средой энергией и информацией. Закрытые (замкнутые) системы изолированны от внешней среды (с точностью принятой в модели).

Целостность

Целостность. Закономерность целостности проявляется в системе в возникновении новых интегративных качеств, не свойственных образующим ее компонентам. Чтобы глубже понять закономерность целостности, необходимо рассмотреть две ее стороны:

1. свойства системы (целого) не являются суммой свойств элементов или частей (несводимость целого к простой сумме частей);

2. свойства системы (целого) зависят от свойств элементов, частей (изменение в одной части вызывает изменение во всех остальных частях и во всей системе).

Существенным проявлением закономерности целостности являются новые взаимоотношения системы как целого со средой, отличные от взаимодействия с ней отдельных элементов.

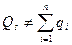
Свойство целостности связано с целью, для выполнения которой предназначена система.

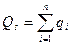Весьма актуальным является оценка степени целостности системы при переходе из одного состояния в другое. В связи с этим возникает двойственное отношение к закономерности целостности. Ее называют физической аддитивностью, независимостью, суммативностью, обособленностью. Свойство физической аддитивности проявляется у системы, как бы распавшейся на независимые элементы. Строго говоря, любая система находится всегда между крайними точками как бы условной шкалы: абсолютная целостность — абсолютная аддитивность, и рассматриваемый этап развития системы можно охарактеризовать степенью проявления в ней одного или другого свойства и тенденцией к его нарастанию или уменьшению.

Для оценки этих явлений А. Холл ввел такие закономерности, как «прогрессирующая факторизация» (стремление системы к состоянию со все более независимыми элементами) и «прогрессирующая систематизация» (стремление системы к уменьшению самостоятельности элементов, т. е. к большей целостности). Существуют методы введения сравнительных количественных оценок степени целостности, коэффициента использования элементов в целом с точки зрения определенной цели.

Интегративность

Интегративность. Этот термин часто употребляют как синоним целостности. Однако им подчеркивают интерес не к внешним факторам проявления целостности, а к более глубоким причинам формирования этого свойства и, главное,— к его сохранению. Интегративными называют системообразующие, снстемоохраняющие факторы, важными среди которых являются неоднородность и противоречивость ее элементов.

Коммуникативность

Коммуникативность. Эта закономерность составляет основу определения системы, предложенного В. Н. Садовским и Э. Г. Юдиным в книге «Исследования по общей теории систем». Система образует особое единство со средой; как правило, любая исследуемая система представляет собой элемент системы более высокого порядка; элементы любой исследуемой системы, в свою очередь, обычно выступают как системы более низкого порядка.

Иными словами, система не изолирована, она связана множеством коммуникаций со средой, которая не однородна, а представляет собой сложное образование, содержит надсистему (или даже надсистемы), задающую требования и ограничения исследуемой системе, подсистемы и системы одного уровня с рассматриваемой.

Иерархичность

Рассмотрим иерархичность как закономерность построения всего мира и любой выделенной из него системы. Иерархическая упорядоченность пронизывает все, начиная от атомно-молекулярного уровня и кончая человеческим обществом. Иерархичность как закономерность заключается в том, что закономерность целостности проявляется на каждом уровне иерархии. Благодаря этому на каждом уровне возникают новые свойства, которые не могут быть выведены как сумма свойств элементов. При этом важно, что не только объединение элементов в каждом узле приводит к появлению новых свойств, которых у них не было, и утрате некоторых свойств элементов, но и что каждый член иерархии приобретает новые свойства, отсутствующие у него в изолированном состоянии.

Таким образом, на каждом уровне иерархии происходят сложные качественные изменения, которые не всегда могут быть представлены и объяснены. Но именно благодаря этой особенности рассматриваемая закономерность приводит к интересным следствиям. Во-первых, с помощью иерархических представлений можно отображать системы с неопределенностью.

Во-вторых, построение иерархической структуры зависит от цели: для многоцелевых ситуаций можно построить несколько иерархических структур, соответствующих разным условиям, и при этом в разных структурах могут принимать участие одни и те же компоненты. В-третьих, даже при одной и той же цели, если поручить формирование иерархической структуры разным исследователям, то в зависимости от их предшествующего опыта, квалификации и знания системы они могут получить разные иерархические структуры, т. е. по-разному разрешить качественные изменения на каждом уровне иерархии.

Эквифинальность

Это одна из наименее исследованных закономерностей. Она характеризует предельные возможности систем определенного класса сложности. Л. фон Берталанфи, предложивший этот термин, определяет эквифинальность применительно к «открытой» системе как способность (в отличие от состояний равновесия в закрытых системах) полностью детерминированных начальными условиями систем достигать не зависящего от времени состояния (которое не зависит от ее исходных условий и определяется исключительно параметрами системы). Потребность во введении этого понятия возникает начиная с некоторого уровня сложности, например биологические системы.

В настоящее время не исследован ряд вопросов этой закономерности: какие именно параметры в конкретных системах обеспечивают свойство эквивалентности? как обеспечивается это свойство? как проявляется закономерность эквивалентности в организационных системах?

Историчность

Время является непременной характеристикой системы, поэтому каждая система исторична, и это такая же закономерность, как целостность, интегративность и др. Легко привести примеры становления, расцвета, упадка и даже смерти биологических и общественных систем, но для технических и организационных систем определить периоды развития довольно трудно.

Основа закономерности историчности — внутренние противоречия между компонентами системы. Но как управлять развитием или хотя бы понимать приближение соответствующего периода развития системы — эти вопросы еще мало исследованы.

В последнее время на необходимость учета закономерности историчности начинают обращать больше внимания. В частности, в системотехнике при создании сложных технических комплексов требуется на стадии проектирования системы рассматривать не только вопросы разработки и обеспечения развития системы, но и вопрос, как и когда нужно ее уничтожить. Например, списание техники, особенно сложной — авиационной, «захоронение» ядерных установок и др.

Формы представления модели

Традиционными формами представления моделей являются системы уравнений в нормальной форме Коши и нелинейные дифференциальные уравнения, графы, структурные схемы. Они позволяют описывать не иерархические модели.

Нормальная форма Коши

Единообразное по форме и удобное для использования матричного аппарата математическое описание динамических (обычно «гладких») систем достигается в пространстве состояний с использованием переменных состояния, т. е. уравнений в форме Коши

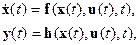(1.1)

где 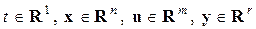векторы переменных состояния, управления и выходов; —  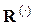 —  -мерное евклидово пространство; 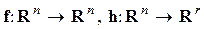гладкие отображения. Предполагается выполнение условия — их — существования решений, а для большинства практических задач единственности. Условия существования и единственности решений выполняются, если 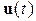принадлежит одному из следующих наиболее часто используемых классов функций: постоянные, кусочно-постоянные, кусочно-непрерывные, кусочно-гладкие, измеримые (локально-ограниченные), а функция 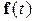удовлетворяет условиям Коши-Липшица — 

В работе [4] приводится классификация форм представления динамических моделей в терминах «вход-состояние-выход», являющихся частными случаями (1.1).

Билинейные системы

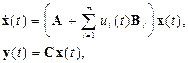
где 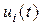скалярные функции, —  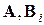числовые матрицы размеров —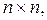 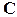 числовая матрица размера —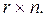 

L-системы

L-системой называется автономная невырожденная система вида

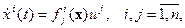
где 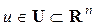, причем

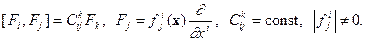
Здесь 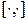является коммутатором алгебры Ли соответствующего векторного поля.

Линейные системы

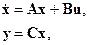
которые приводятся к L-системам 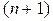-го порядка вида

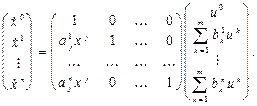
Линейно-аналитические системы

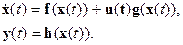
Если 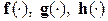полиномы, то система называется —  полиномиальной [132, 141, 161].

Системы с управлением, входящим линейно (правоинвариантные, аффинные) (векторное представление)

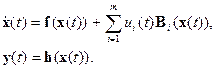
Системы управления с функциональными коэффициентами при переменных состояния и управления (матричное представление)

В ряде работ [43, 51, 52] принимается следующее описание

в векторно-матричной записи

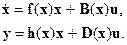
Переход от векторного к матричному представлению осуществляется с помощью интегрального преобразования [11]

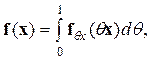
где 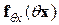матрица Якоби, найденная по —  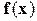из (1.12б).

Нормальная форма Коши (НФК) удобна для представления модели в алгорит­мах явного типа, и позволяет широко применять богатую матричную арифме­тику соврем