Кинематические цепи и их классификация.

Кинематические цепи и их классификация.

Кинематическая цепь – это система звеньев, связанных между собой кинематическими парами. Любой механизм представляет собой кинематическую цепь (к. ц.) звеньев, соединенных в кинематические пары (к.п.). К. ц. могут быть простыми и сложными, открытыми и замкнутыми, плоскими и пространственными. В простой к. ц. каждое из ее звеньев входит в состав одной или двух к. п., а в сложной к. ц. имеются звенья, входящие в состав трех и более к. п. В открытой к. ц. имеются звенья, входящие в состав одной к. п., а в замкнутой цепи каждое звено входит в состав 2-х и более к. п. (рис.6,а-в). Если точки всех звеньев двигаются в одной или параллельных плоскостях, то к. ц. называется плоской, в противном случае к. ц. – пространственная (точки звеньев описывают плоские кривые в непараллельных плоскостях или пространственные кривые).

Кинематический анализ плоских рычажных механизмов аналитическим методом.

Графический (метод диаграмм) и графоаналитический методы (метод планов скоростей и ускорений) кинематического анализа механизмов имеют недостатки: невысокая точность, определяемая точностью графических построений, и большая трудоёмкость. При иcпользовании графического метода необходимо построить диаграммы перемещений, скоростей и ускорений для каждой исследуемой точки механизма, а при использовании графоаналитического метода – несколько планов скоростей и ускорений механизма, чтобы определить динамику изменения скорости и ускорения интересующих нас точек (т.е. при различных положениях механизма).

Эти недостатки отсутствуют в аналитическом методе. Но при этом необходимо составлять достаточно сложные аналитические зависимости (формулы) и иметь возможность решать их с использованием компьютерных техники и технологии, что в последнее время возможно и доступно.

Методы аналитического исследования:

метод замкнутых векторных контуров (метод Зиновьева) удобен для кинематического анализа практически всех используемых в технике несложных рычажных механизмов;

метод преобразования координат (метод Морошкина) удобен для кинематического анализа многозвенных механизмов типа манипуляторов промышленных роботов.

Виды зубчатых передач. Передаточное отношение, передаточное число.

Зубчатые механизмы предназначены для передачи вращательного движения от одного вала к другому. Цилиндрические – передают вращение между параллельными валами. Могут передавать большие нагрузки и достаточно просто изготавливаются. Зуб – это выступ на звене для передачи движения посредством взаимодействия с соответствующим выступом другого звена. Зубчатое звено – звено, имеющее один или несколько зубьев. Зубчатое колесо – зубчатое звено с замкнутой системой зубьев, обеспечивающее непрерывное движение другого звена. Зубчатая передача – трехзвенный механизм; в котором два сдвижных звена являются зубчатыми колесами образующими с неподвижным звеном вращательную или поступательную пару.

Цилиндрические передачи классифицируют:

· по пространственному расположению – на внешние, внутренние и реечные.

· по форме зуба – на прямо- и косозубые. У первых линия зуба паралл. оси колеса, у вторых – расположена под углом.

· по боковой поверхности – на эвольвентные, зацепление Новикова (боковая поверхность очерчена по дуге окружности) и др.

· по передаточному отношению.

Передаточное отношение - это отношение угловой скорости ведущего зубчатого колеса к угловой скорости, ведомого зубчатого колеса. U1=-w1/w2 – для внешнего зацепления; U1= w1/w2 – для внутреннего. Передаточное число – отношение числа зубьев колеса к числу зубьев шестерни. Колесо - зубчатое колесо передачи с большим числом зубьев. Шестерня - колесо с меньшим числом зубьев. Различают передачи с положительным и отрицательным передаточным отношением, с U>1 (редукторы) и U<1 (мультипликаторы).

Методичка динамика стр 14

Режимы движения машин стр 304. Коэффициент неравномерности движения.

Методичка динамика страница 20

Силовой расчет механизмов

Силовой расчет механизмов относится к решению первой задачи динамики, первая задача включает в себя две части: изучение сил, действующих на звенья механизма; определение неизвестных сил при заданном законе движения на входе (эта вторая часть и есть задача силового расчета).

С точки зрения решения задач динамики силы (в данном случае под силой понимается обобщенное понятие силового фактора – собственно сила или момент) можно классифицировать следующим образом:

а) по взаимодействию звена механизма с другими объектами. По этому признаку силы подразделяются на внешние и внутренние:

- внешние силы – это силы взаимодействия звена механизма с какими-то телами или полями, не входящими в состав механизма;

- внутренние силы – это силы взаимодействия между звеньями механизма (реакции в кинематических парах);

- движущая сила – это сила, которая помогает движению звена и развивает положительную мощность;б) по мощности, развиваемой силой. По этому признаку силы делятся на силы движущие и силы сопротивления (рисунок 16):

- сила сопротивления препятствует движению звена и развивает отрицательную мощность.

Рисунок 16

В свою очередь силы сопротивления можно разделить на силы полезного сопротивления и силы вредного сопротивления:

- силы полезного сопротивления – это силы, для преодоления которых и создан механизм. Преодолевая силы полезного сопротивления, механизм создает полезную работу (например, преодолевая сопротивления резанию на станке, добиваются необходимого изменения формы детали; или, преодолевая сопротивление воздуха в компрессоре, сжимают его до требуемого давления и т.д.);

- силы вредного сопротивления – это силы, на преодоление которых затрачивается мощность и эта мощность теряется безвозвратно. Обычно в качестве вредных сил сопротивления выступают силы трения, гидравлического и аэродинамического сопротивлений. Работа по преодолению этих сил переводится в тепло и рассеивается в пространство, поэтому коэффициент полезного действия любого механизма всегда меньше единицы;

в) силы веса – это силы взаимодействия звеньев механизма с гравитационным полем земли;

г) силы трения – силы, сопротивляющиеся относительному перемещению соприкасающихся поверхностей;

д) силы инерции – силы, возникающие при неравномерном движении звена и сопротивляющиеся его ускорению (замедлению). Сила инерции действует на то тело, которое заставляет ускоряться (замедляться) данное звено. В общем случае при неравномерном движении возникает сила инерции и момент сил инерции:

F_ин=-m ^. a_s , M_ин=-I_s ^. e ,

где

F_ин – главный вектор сил инерции, приложенный в центре масс звена;

M_ин – главный момент сил инерции;

m – масса звена;

I_s – момент инерции звена относительно центра масс;

a_s – ускорение центра масс звена;

e – угловое ускорение звена.

Знак минус в формулах показывает, что сила инерции направлена противоположно ускорению центра масс звена, а момент сил инерции направлен противоположно угловому ускорению звена. Знак силы или момента учитывается только при установлении истинного направления силы или момента на расчетной схеме, а в аналитических вычислениях используется абсолютные их значения.

Рисунок 17

При силовом анализе механизмов могут встретиться различные случаи, когда один или оба силовых инерционных фактора могут иметь нулевое значение. На рисунке 17, приведенном выше, показаны некоторые случаи возникновения сил и моментов сил инерции при движении звеньев механизма.

Непосредственно силовой расчет сводится к определению неизвестных сил, действующих на звенья механизма. Как известно из теоретической механики для определения неизвестных сил используются уравнения статики.

Механизм же является неравновесной системой, т.к. большинство его звеньев имеет неравномерное движение, а точки, принадлежащие этим звеньям, движутся по сложным криволинейным траекториям (состояние равновесия – это состояние покоя или прямолинейного равномерного движения).

Поэтому для решения поставленной задачи применяется метод кинетостатики. Метод кинетостатики основан на принципе Даламбера: если ко всем внешним силам, действующим на звенья механизма, добавить силы инерции и моменты сил инерции, то данный механизм будет находиться в состоянии статического равновесия. То есть это искусственный прием, приводящий неравновесную систему в состояние равновесия.

Искусственность приема заключается в том, что силы инерции прикладываются не к тем телам, которые заставляют двигаться звенья ускоренно (замедленно), а к самим звеньям.

Применив этот прием, в дальнейшем можно производить силовой расчет с использованием уравнений статики. Однако, чтобы решить задачу с помощью только уравнений равновесия, система должна быть статически определимой.

Условие статической определимости плоской кинематической цепи:

Для каждого звена, расположенного в плоскости, можно составить три независимых уравнения статики. Если в кинематической цепи имеется "n" подвижных звеньев, то в совокупности для этой цепи можно записать 3n независимых уравнений статики (равновесия). Эти уравнения используются для определения реакций в кинематических парах и неизвестных внешних сил.

На плоскости существуют кинематические пары только пятого и четвертого классов. Пары пятого класса представлены вращательной кинематической парой (шарниром) и поступательной парой (соединение ползуна с направляющей). В шарнире усилие между звеньями может передаваться в любом направлении, поэтому у реакции в шарнире неизвестными являются величина и направление (два компонента), т.е. для определения полной реакции во вращательной паре надо затратить два уравнения статики.

В первом приближении расчет ведется без учета сил трения. В этом случае перемещению ползуна вдоль направляющей ничто не препятствует. Перемещаться же поперек направляющей и поворачиваться ползун не может, поэтому в поступательной паре реакция направлена перпендикулярно направляющей и возникает реактивный момент, препятствующий повороту ползуна.

При силовом расчете обычно реактивный момент не определяют, а находят условную точку приложения реакции (произведение реакции на расстояние до ее условной точки приложения и есть реактивный момент). На определение реакции в поступательной паре также надо затратить два уравнения статики (определить два компонента – величину и точку приложения). Таким образом, на определение полной реакции в кинематической паре пятого класса необходимо затратить два уравнения статики.

Пары четвертого класса (высшие пары) на плоскости представляют соприкасающиеся между собой профили. В высшей паре усилие между звеньями передается по общей нормали к касающимся профилям (без учета сил трения). Поэтому в высшей паре четвертого класса реакция неизвестна только по величине (точка приложения реакции в точке контакта профилей, направление вдоль общей нормали к этим профилям).

Таким образом, для определения реакции в паре четвертого класса надо затратить одно уравнение статики (определить один компонент – величину реакции).

Если в кинематической цепи количество пар пятого класса равно Р₅ , то на определение реакций во всех этих парах надо затратить 2Р₅ уравнений статики. На определение реакций во всех парах четвертого класса используется число уравнений, равное количеству этих пар Р₄ .

Таким образом, из 3n независимых уравнений статики 2Р₅ уравнений используются для определения реакций в парах пятого класса и Р₄ – для определения реакций в парах четвертого класса. Оставшиеся уравнения используются для определения неизвестных внешних сил, действующих на звенья механизма.

Пусть X – число уравнений, оставшихся для определения неизвестных внешних сил, тогда

X=3n–2Р₅–Р₄,

но эта формула совпадает с формулой Чебышева для определения числа степеней свободы плоской кинематической цепи. В результате можно сформулировать условие статической определимости кинематической цепи следующим образом: кинематическая цепь статически определима в том случае, когда число неизвестных внешних сил, действующих на ее звенья, не превышает числа степеней свободы этой цепи.

Так как методы решения разработаны для групп Ассура, то необходимо сформулировать условие статической определимости группы Ассура. Группа Ассура – это кинематическая цепь, имеющая собственную степень свободы, равную нулю. Поэтому группа Ассура статически определима, если на ее звенья не действуют неизвестные внешние силы. Уравнений в группе Ассура достаточно лишь для определения реакций в кинематических парах. Это обстоятельство предопределяет порядок силового расчета механизма:

- разбивают механизм на группы Ассура, взяв в качестве начального то звено, на которое действует неизвестная внешняя сила;

- решение начинают с последней присоединенной группы и заканчивают начальным звеном.

При таком подходе на группы Ассура всегда будут действовать только известные внешние силы и из рассмотрения их равновесия будут определены реакции в кинематических парах, а из рассмотрения условий равновесия начальных звеньев будут определены оставшиеся реакции и неизвестные внешние силы.

Поскольку решение ведется по группам Ассура, то ниже рассматривается принцип силового расчета групп на примере групп второго класса.

Уравновешивание механизмов

Целью уравновешивания механизмов является устранение переменных во времени и пространстве воздействий стойки, станины механизма на опору, фундамент, вызывающих колебания фундамента и здания, а также уменьшение вибрации.

Рис. 6.4

Приведённые массы в точках В и С равны:

;

.

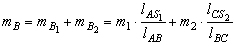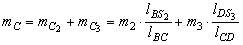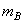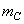Так как заменяющие массы и совершают вращательное движение, то для уравновешивания сил инерции необходимы противовесы с массам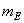и и 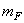, определяемыми из условий (рис. 6.4, б):

; ,

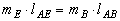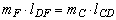где, задавая длины противовесов, можно получить их массы и наоборот.

Рассмотрим моментное уравновешивание на примере четырёхшарнирного механизма. Его приближённое моментное уравновешивание можно осуществить после статического уравновешивания, введя в схему механизма два одинаковых дополнительных противовеса 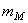(рис. 6.5), соединённых с зубчатыми колёсами “a” и “b”. Колесо “a” жёстко связано с кривошипом 1 и вращается с угловой скоростью 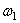, а равное ему колесо “b” вращается с той же угловой скоростью 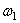, но угловые координаты противовесов отличаются на 180⁰, поэтому момент пары сил инерции от противовесов 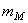равен 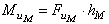. Подбирая положение точки E, можно обеспечить направление 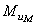, противоположное направлению 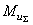, а массу противовесов 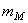определяют из условия .

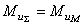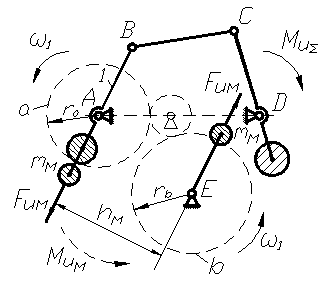
Рис.6.5

Рис.6.6

При проектировании детали типа кулачка уравновешиваются так: в деталь с центром на оси вращения вписывается окружность, подсчитываются площади ограниченные контуром кулачка и расположенные вне или внутри окружности, определяется массы и центры масс 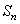неуравновешенных частей кулачка, находится эксцентриситет 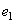центра масс 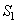кулачка по величине и направлению и определяется его дисбаланс с помощью корректирующей массы 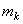, размещаемой на эксцентриситете 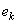, создается дисбаланс 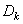равный по величине и противоположный по направлению .

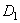Рис.6.7

На детали выбирают две плоскости коррекции и каждый вектор дисбаланса раскладывают на две составляющие, расположенные в плоскостях коррекции. Затем составляющие векторы дисбалансов в плоскостях коррекции суммируются и их равнодействующий дисбаланс, например, , уравновешивается соответствующей корректирующей массой .Пример такого уравновешивания изображен на рис. 6.7.

Статическое уравновешивание масс плоских рычажных механизмов (ме­тодом статического размещения масс).

Коэффициент формы зуба

Геометрическая форма зуба в значительной мере определяет показатели его как изгибной, так и контактной прочности. Оценка влияния геометрии зуба на изгибную прочность осуществляется коэффициентом формы зуба Y. Этот коэффициент определяется через параметры балки параболиче-

ского сечения (балки равного сопротивления изгибу), которая вписывается в контур зуба так, чтобы вершина параболы располагалась в точке пересечения оси зуба и нормали к профилю в вершине, а ветви касались профиля зуба у основания ( см. схему на рис. 13.4). где Sp - толщина зуба по хорде на окружности, проходящей через точки касания параболы и профиля зуба, l - высота от вершины параболы до хорды Sp .

Кинематические цепи и их классификация.

Кинематическая цепь – это система звеньев, связанных между собой кинематическими парами. Любой механизм представляет собой кинематическую цепь (к. ц.) звеньев, соединенных в кинематические пары (к.п.). К. ц. могут быть простыми и сложными, открытыми и замкнутыми, плоскими и пространственными. В простой к. ц. каждое из ее звеньев входит в состав одной или двух к. п., а в сложной к. ц. имеются звенья, входящие в состав трех и более к. п. В открытой к. ц. имеются звенья, входящие в состав одной к. п., а в замкнутой цепи каждое звено входит в состав 2-х и более к. п. (рис.6,а-в). Если точки всех звеньев двигаются в одной или параллельных плоскостях, то к. ц. называется плоской, в противном случае к. ц. – пространственная (точки звеньев описывают плоские кривые в непараллельных плоскостях или пространственные кривые).