Замена переменных в определенном интеграле.
[T] пусть функция f(x) непрерывна на сегменте [a,b] и пусть выполнены следующие условия:
1) функцию х=j(t) дифференцируема на [a,b] и j’(t) непрерывна на [a,b]
2) Множеством значений функции х=j(t) является отрезок [a,b]
3) j(a)=a и j(b)=b, то справедлива формула 
Доказательство: По формуле Ньютона- Лейбница: 
, где F(x)-какая-нибудь первообразная для функции f(x) на [a,b]. С другой стороны, рассмотрим сложную функцию Ф(t)=F(j(t)) Согласно правилу дифференцирования сложной функции находим: Ф’(t)=F’(j(t))*j’(t)=f(j(t))j’(t). Отсюда следует, что функция Ф(t) является первообразной для функции f(j(t))j’(t), непрерывной на [a,b] и поэтому согласно формуле Ньютона-Лейбница получаем, 
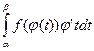= Ф(b)-Ф(a)=F(j(b))-F(j(a))=F(b)-F(a)=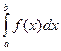 
Это формулы замены переменной или подстановки в определенном интеграле.
Замечание1. Если при вычислении неопределенного интеграла с помощью замены переменной мы должны были от новой переменной t возвращаться к старой переменной х, то при вычислении определенного интеграла этого можно не делать, т.к. цель- найти число, которое в силу доказанной формыл равно значению каждого из рассматриваемых интегралов.
Формула интегрирования по частям в определенном интеграле.
[T] Если функция u(x) и v(x) имеют непрерывные производные на сегменте [a,b] то справедлива формула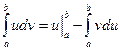 
Доказательство Так как функция u(x) и v(x) по условию имеют производные, то по правилу дифференцирования произведения [u(x)v(x)]’=u(x)v’(x)+v(x)u’(x). Откуда следует, что функция u(x)v(x) является первообразной для функции u(x)v’(x)+v(x)u’(x). А т.к. функция u(x)v’(x)+v(x)u’(x) непрерывна на отрезке [a,b], то интеграл от нее существует, т.е. она интегрируема на этом отрезке и по формуле Ньютона-Лейбница 
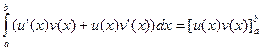Отсюда по свойству 4 определенных интегралов получим, что то же 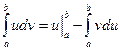, ч т.д.
Приложение определенного интеграла Рассмотрим криволинейную трапецию, ограниченную снизу сегментом [a,b] оси Ох, с боков прямыми x=a, x=b и графиком непрерывной и неотрицательной функции y=f(x) на [a,b]. Докажем, что площадь этой криволинейной трапеции S=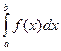
Доказательство: Разобьем произвольно отрезок [a,b] на n частей, т.е. рассмотрим разбиение сегмента [a,b] на {Xn} точками a=Xo<X1<X2<…<Xi-1<Xi<…<Xn=b, выберем на каждом частичном отрезке [Xi-1, Xi], I=1,2,…,n? Произвольно точку xI (Xi-1£xI£Xi) и рассмотрим ступенчатую фигуру. Ее площадь будет приблизительно равной площади криволинейной трапеции. S» 
, где Dхi= хi- хi-1.Таким образом, получена интегральная сумма s. Т.к. Функция f(x) непрерывна на [a,b], то предел этой суммы существует при c= 
и площадь S криволинейной трапеции численно равна определенному интегралу от функции f(x) на [a,b] S=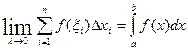 
Геометрический смысл определенного интеграла: определенный интеграл от неотрицательной непрерывной функции f(x) на [a,b] численно равен площади криволинейной трапеции с основанием [a,b] ограниченной сверху графиком функции y=f(x).