Понятие неопределенного интеграла.

Понятие неопределенного интеграла.

Def Если функция F(x) является первообразной для функции f(x) на промежутке Х, то множество функций {F(x)+C}, где С- произвольная постоянная называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом òf(x)dx=F(x)+C. При этом f(x) называется подынтегральной функцией, f(x)dx- подынтегральным выражением, а переменная х- переменная интегрирования. òf(x)dx- выражает множество всех первообразных для функции f(x) на промежутке Х.

DefВосстановление функции по ее производной или что тоже самое: отыскание неопределенного интеграла называется интегрированием этой функции, т.к. F’(x)=f(x) òF’(x)dx=F(x)+C

Интегрирование- операция обратная дифференцированию и правильность интегрирования определяется следующим образом: мы должны продифференцировать результат и если получили подынтегральную функцию, то операция выполнена верно.

Основные свойства неопределенного интеграла:

1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. (òf(x)dx)’=f(x) и d( òf(x)dx)=f(x)dx Док-во: (òf(x)dx)’=(F(x)+C)’=F’(x)=f(x) и dòf(x)dx=(òf(x)dx)’dx=f(x)dx

2. d(òf(x)dx)=f(x)dx, дифференциал от неопределенного интеграла на промежутке Х равен подынтегральному вырожению.

Док-во: d(òf(x)dx)=d(F(x)+C)=(F(x)+C)’dx=F’(x)dx=f(x)dx

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. òdF(x)=F(x)+C. Док-во: т.к. òdF(x)=F’(x)dx, то по определению òF'(x)dx=F(x)+C

4. Постоянный множитель можно вынести из-под знака интеграла, т.е. если k=const¹0, то òkf(x)dx=kòf(x)dx. Док-во: пусть F(x) первообразная для f(x) на промежутке Х, т.е. "xÎX F’(x)=f(x)ÞkF(x) первообразная для kf(x), т.е. (kF(x))’=kF’(x)=kf(x). Из определения следует, что kòf(x)dx=k[F(x)+C]=kF(x)+C1=òkf(x)dx, где С1=кС, ч.т.д.

5. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно, т.е. ò(f(x)±g(x))dx=òf(x)dx±òg(x)dx. Док-во: пусть F(x) и G(x) являются первообразными для функций f(x) и g(x) на промежутке Х, т.е. "хÎХ F’(x)=f(x), G'(x)=g(x). Тогда функции F(x)±G(x) являются первообразными для функция f(x)±g(x). Следовательно, òf(x)dx±òg(x)dx=(F(x)+C1)±(G(x)+C2)=(F(x)±G(x))+(C1±C2)=[F(x)±G(x)]+C=ò(f(x)±g(x))dx

Это свойство справедливо для любого конечного числа слагаемых.

Методы замены переменной

1. Непосредственное интегрирование.

С помощью табл осн интегралов.

2. Метод подстановки или метод замены переменных.

Достаточно часто введение новой переменой позволяет свести интеграл к табличному

[Т] Пусть функция х=j(t) определена и дифференцируема на некотором промежутке Т и пусть Х- множество значений этой функции, на котором определена функция y=f(x), т.е. на T определена сложная функция y=f[j(t)]. Тогда если на множестве Х функция f(x) имеет первообразную F(x), то справедлива формула òf(x)dx|_x=j(t)= òf[j(t)]j’(t)dt. Док-во: Пусть функция F(x) является первообразной для функции f(x) на множестве Х. Рассмотрим на множестве T сложную функцию F[j(t)]. Продифференцируем ее по правилам дифференцирования сложной функции: F’[j(t)]*j’(t)=f’[j(t)]*j’(t)Þ мы получили что эта функция имеет на множестве Т первообразную F[j(t)]. òf[j(t)]*j’(t)dt=F[j(t)]+C=F(x)+C|_x=j(t)= òf(x)dx|_x=j(t). Получили искомую формулу замены переменных в неопределенном интеграле.

Замечание: При замене переменныхв неопределенном интеграле иногда более удобно задавать не х как функцию t, а задавать t как функцию от х.

Метод неопределенных коэффициентов.

Метод неопределенных коэффициентов

Он заключается в том, чтобы следовать алгоритму: Записать представление 1, привести правую часть к общему знаменателю и группировать при степенях Х, получим дроби с равными знаменателями, присваиваем числители. Получим 2 многочлена, они равны если равны коэффициенты при соответствующих степенях Я, следовательно составляем систему уравнений, приравнивая коэффициенты при соответствующих степенях Х.

Доказательство:

1 вариант (учебники): возьмем любое значение xÎ[a,b] и придадим ему приращение 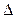х¹0 такое, чтобы х+ 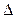хÎ[a,b], т.е. a£x+ 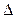х£b. Тогда функция Ф(х) по определению получит новое значение: Ф(х+ 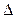х)=

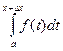
Согласно второму свойству определенного интеграла, имеем: Ф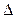(х+ х)= 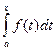+ 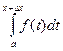=Ф(х)+ 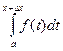DФ=Ф(х+DХ)-Ф(х),
т.к. f(x) непрерывна на [a,b] то существует число cÎ[x, x+Dx]:[ 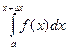=f(c)Dx]. Если устремить приращение аргумента к нулю, получим : 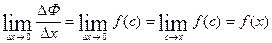=f(x) или Ф’(х)=f(x), ч т.д. Можно записать, что òf(x)dx=Ф(x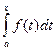)+C= +C

2 вариант (Деревенских) Ф’(х)= 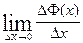DФ(х)= 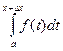- 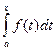= 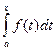+ 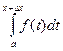- 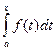= =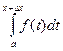f(c)* Dx. По теореме о среднем существует cÎ[x, x+Dx]

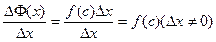Ф’(x)= 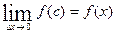Отсюда следует, что Ф’(x)=f(x)

Формула Ньютона-Лейбница.

Пусть функция f(x) непрерывна на отрезке [a,b] и имеет на этом отрезке семейство первообразных, одной из которых является Ф(х)= .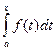

[Т] Если функция f(x) непрерывна на [a,b], то верно следующее равенство 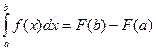. Т.е. определенный интеграл от непрерывной функции равн разности значений любой ее первообразной на верхнем и нижнем пределах интегрирования соответственно. Она называется формулой Ньютона-Лейбница.

Доказательство: Пусть F(x) другая первообразная для функции f(x) на том же отрезке, которая отличается от Ф(х) не более чем на константу, т.е. Ф(х)=F(x)+C, 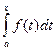=F(x)+C, где С- некоторое число, a£x£b. Подставляя в это равенство значение х=а и используя свойство 1, имеем: 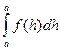=0, получим: 0= 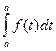, F(a)+C, C=-F(a)

Т.е. для любого хÎ[a,b] 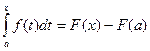Полагая здесь х=b получим искомую формулу.

А R

DEF

Предел интеграла при e®0 называется несобственным интегралом второго рода и обозначается . Если этот предел конечный, то говорят что интеграл существует или сходится, а функцию f(x) называют интегрируемой на промежутке [a,b), если предела нет или он бесконечен, то говорят что интеграл расходится. Аналогично, если особой является точка х=а, то несобственных интеграл второго рода определяется как Если функция f(x) не ограничена в окрестности некоторой внутренней точки сÎ[a,b], то по определению полагают 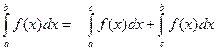, где несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам предыдущим. Если а и b особые точки, т.е. функция f(x) ограничена и интегрируема на интервале (a,b), то несобственный интеграл второго рода определяется в виде суммы 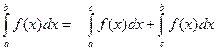, где с- произвольная точка на (a,b), а несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам.

19. Метрические, линейные, нормированные, евклидовы пространства.

Функции многих переменных:

Пусть у=f(x), D(f)=XÌR, Е(f)=YÌR

Y=f(x1, x2, … xn) это точки n-мерного Эвклидового пространства

Метрические пространства.

На множестве Х определена фигура метрического пространства, если задана функция r(x,y) двух произвольных элементов этого множества, удовлетворяющих следующим аксиомам:

1. 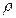(x,y)=0 тогда и только тогда, когда x=y

3. r(x,y)£r(x,z)+r(z,y) (неравенство )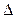

r(х,y) функция метрики или функция расстояния между точками х и у, принадлежащих Х.

Т.о. метрическое пространство R образует множество Х, с введенной на этом множестве функции расстояния метрического пространства R=(X, r). Если положим, что х=у, то 0£r(x,z)+r(z,y)

Р(x,y) функция метрики или функция расстояния между точками х и у, принадлежащих Х. Т.о. метрическое пространство R образует множество Х, связанной на этом множестве функции расстояния метрического пространства R=(X,р)

Если положим, что х=у, то 0£р(xz)+p(z,x)

2p(x,z)>0 метрика не отрицательна

Введем понятие n-мерного координатного пространства Аⁿ

Def M-мерным координатным пространством А^m называется множетсво всевозможных упорядоченных совокупностей m действительных чисел (x1, x2, x3,…, xm)

Каждую упорядоченную совокупность (x1, x2,…,xm) называют точкой этого пространства и обозначают одной буквой М, при этом числа x1, x2, …,xn называются координатами точки М, что символически записывается так М( x1, x2,…xn)

Чтобы множество Х было метрическим пространством нужно:

Выберем в качестве множества Х n- мерное координатное пространство, возьмем люые х,у принадлежащие этому пространству. Х(х1…хn), y(y1..yn)

Введем функцию расстояния на Х между х и у. Р(х,у)=

Линейное пространство L

Множество элементов L, содержащее хотя бы один элемент, называется линейным или векторным пространством, если выполнены следующие аксиомы:

1. Любые x,y принадлежат L, однозначно определен 3 элемент z, называемый их суммой, обозначаемый z=x+y, причем справедливые следующие свойства:

А) х+у=у+х (ассоциативность)

Б) (х+у)+z=x+(y+z)

В) Существует элемент (его обычно обозначают за 0) такой, что x+0=X

Г) Существует элемент Х, называемый противоположным, такой что x+x’=0

2) Для любого числа a и любого элемента х принадлежащего L определен элемент у из множества L= ax при этом справедливы следующие свойства:

a(b^х)=(ab)^х

(b+a)х=aх+bх

a(х+у)=aх+aу

1*x=x

х=х, где ab некоторые числа, х и у точка множества L. Если в аксиоме b и a принадлежат множеству вещественных чисел, то множества L называется действительным линейным пространством

Нормированное пространство N

Возьмем функция f(x)=||x||, ставящая каждому элементу х из множества L в соответствие вещественное число x принадлежащее L – называется нормой в линейном пространстве L, если выполнены следующие аксиомы:

1.f(x)=||x||=0 тогда и только тогда, когда х=0

2. f(aх)=|a|*||x||=|a|*f(x)

3. f(x+y)=||x+y||£||x|| +||y||=f(x)+f(y)

Пространство L, сведенное на этом множестве функцией норма X называют нормированным пространством и обозначают через N. ||x||>0

Следует отметить, что в любом норм. Пространстве может быть введена функция расстояния b(x,y)=||x*y|| как норма элемента х и у.

Def Координатное пространство Аⁿ называют n- мерным евклидовым пространством, если между двумя любыми точками х(х1, х2, …, хn) и у(у1, у2…уn) введена функция расстояния р(х,у) по формуле р(х,у)=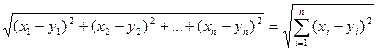

Обозначается n- мерное Евклидово пространство через Еⁿ

Следует отметить, что в этом пространстве могут быть ||x-y||=p(x,y)

Метрические пространства.

Будем говорить, что на множестве Х определена структура метрического пространства, если задана ф-я r(х,у) двух элементов х,уÎХ, удовлетворяющих следующим аксиомам:

1.r(х,у)=0 тогда и только тогда, когда х=у

2.r(х,у)=r(у,х) – аксиома симметрии

3.r(x,z)£r(x,y)+r(x,z)

Ф-я r(х,у) – метрика или ф-я расстояния между точками х,уÎХ.

Т.о. метрическое пространство R=(X,r): ф-я Х с введенной на этом множестве функцией метрикой.

r(х,х)£r(х,у)+r(у,х)

0£2r(х,у)

r(х,у)³0

Примеры:

1).X=R=E¹ (множество рациональных чисел)

r(х,у)=|х-у| - удовлетворяет условиям.

2). n-мерным пространством Аⁿ называют множество всевозможных упорядоченных совокупностей n вещественных чисел (х₁, х₂,…,х_n). Каждую упорядоченную совокупность называют точкой n-мерного пространства, а точки х₁, х₂,…,х_n – координатами точки. На Аⁿ, например, метрика:

n

r(х,у) = å((x_i-y_i)²)^1/2

i=1

Линейные пространства.

Множество элементов L, содержащее хотя бы 1 элемент называется линейным или векторным пространством, если выполнены следующие аксиомы:

1. Аксиомы сложения. Для любых двух элементов х,уÎL однозначно определен третий элемент z, называемый их суммой и обозначаемый z=x+y, и справедливы следующие свойства:

а)х+у = у+х

б)(x+y)+z = x+(y+z)

в)$ элемент, называемый нулевым и обозначаемый 0, такой, что для любых хÎL: х+0 = х

г) Для любого хÎХ $ элемент х¹, называемый противоположным, такой, что х+х¹ = 0

2. Аксиомы умножения на число. Для любого числа а и любого хÎL, определен элемент уÎL, называемый умножением числа а на элемент х и обозначаемый а*х, обладающий следующими свойствами (для любых чисел а, b и любых х,уÎL):

а) a(bx) = ab(x)

б) (a+b)x = ax+bx

в) a(x+y) = ax+ay

г) 1*x = 1

Замечание: если в аксиомах 2 a,bÎR, то линейное пространство называют действительным или вещественным линейным пространством.

Примеры:

1). А¹=R. В кач-ве операций сложения – сложение вещественных чисел; в кач-ве операций умножения – умножение вещественных чисел .

2). Aⁿ

1)а) z = x+y = (x₁+y₁, x₂+y₂,…,x_n+y_n) и так далее все свойства 1) и 2) групп по аналогии.

Нормированные пространства.

F(x) = ||x|| - “норма икс”, ставящая в соответствие любому хÎL (линейн. простран.) вещественное число ||х||, наз. нормой в лин. Пространстве, если она удовлетворяет следующим аксиомам:

1. ||х|| = 0 тогда и только тогда, когда х = 0

2. f(ax) = ||ax|| = ||a||*||x|| = |a|*f(x)

3. f(x+y) = ||x+y|| £ ||x||+||y|| = f(x)+f(y) (x,y - точки)

N – нормированное пространство.

||x||³0

В любом N может быть введена ф-я метрики r(x,y) = ||x-y|

Пример: А¹=R=L. F(x) = ||x||=|x| - удовлетворяет условиям.

n-мерное Евклидово пространство.

Координатное пространство Аⁿ называют n-мерным Евклидовым пространством и обозначают Еⁿ, если между двумя его точками ХÎЕⁿ и YÎЕⁿ введена ф-я расстояния r(х,у) по формуле:

n

||x|| = (å(x_i-y_i)²)^1/2

i=1

Еⁿ можно считать нормированным пространством, у которого

||x-y|| = r(x,y)

Неявные функции.

Def Если переменная u, являющаяся по смыслу функцией переменных х1,х2,…,хn задается посредством функций уравнений F(U,X1,x2,…,xn)=0, то говорят, что функция задана неявно.

Частные производные неявно заданной функции вычисляются по формулам:

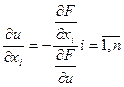
Рассмотрим совокупность М неявных функций, которые задаются посредством системы М функциональных уравнений:

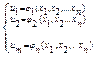(1)

Пусть функции определены, как решение М функциональных уравнений (2)

(2)

Решением системы (2) будет называться совокупность функций, таких что при их подстановки в систему все уравнения этой системы образуются в тождества.

Def Это решение будем называть непрерывным и дифференцируемом в некоторой области D изменения переменных Х1,Х2,…Хn Если каждая из функций U1,U2,…Um непрерывна и дифференцируема в этой области.

=

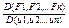
Такой определитель называют определителем Якоби или Якобианом.

[T] Система (2) будет разрешима, а решение непрерывно и дифференцируемо, если функция f1,f2,…,fn дифференцируема в окрестности точки Мо, 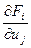непрерывна в точке Мо, Якобиан 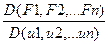отличен от 0 и F1=F2=…=Fn в точке Мо

Условный экстремум

Задача отыскания экстремума функции аргументы которой удовлетворяют дополнительному условию связи называется задачей отыскания условного экстремума.

Рассмотрим вопрос отыскания экстремума функции z=f(u1,u2,…um,x1,x2,…,xn)

Будем говорить, что эта функция при наличии условий связи (2) имеет условный максимум (минимум) в точке Мо, координаты которой удовлетворяют этим условиям связи, если существует окрестность точки Мо, для которой значение этой функции в точке Мо является наибольшим (наименьшим) среди всех точек координаты которых удовлетворяют эти условиям связи.

Первый способ решения задачи условного экстремума:

Основная его идея – переход от задачи условного экстремума к задаче безусловного экстремума.

Пусть у функции F1, F2, …Fm дифференцируема в окрестности точки Mо и 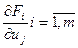непрерывны в окрестности точки Мо. Пусть, кроме того, Якобиан 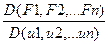неравен 0 в точке Мо. Тогда система (2) имеет непрерывное дифференцируемое решение 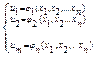. Подставим это решение в функцию 2: z=

Метод множителей Лагранжа.

Метод неопределенных множителей Лагранжа. Если система функций уравнений (2) неразрешима, либо ее решение затруднительно для вас, используют более универсальный способ – метод неопределенных множителей Лагранжа. Идея та же – переход от условного экстремума к безусловному.

L=f+l1F1+l2F2+…+lmFm (4)

Функция Лагранжа.

Теперь находим экстремум этой функции. Здесь l1, l2,…ln –множители Лагранжа.

Предположим, что функция дифференцируема

L(u1,u2,…um,x1,x2,…,xn,l1,l2,…ln)

Необходимые условия экстремума:

Эта система содержит u+2m уравнений и u+2m переменных.

Мо(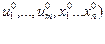

lо(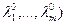

Для полученных точек проверяем достаточное условие экстремума.

Признак сравнения.

Пусть для двух рядов си неотрицательными членам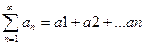и (1)и 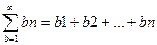(2)выполняется неравенство a£b для всех n. Тогда из сходимости ряда (2) следует сходимость ряда (1), а расходимость ряда (1) влечет за собой расходимость ряда (2)

Доказательство: Пусть Sn и Sn’ частичные суммы соответственно рядов 1 и 2. Из условия теоремы следует, что Sn£Sn’ Если ряд 2 сходится, то по теореме о необходимом и достаточном условии сходимости ряда последовательность {Sn’} ограничена, значит, монотонная последовательность {Sn} также ограничесна, т.е. она также сходится. Если ряд 1 расходится, то ряд 2 не может сходиться, иначе в силу первой части доказательства будет сходится и ряд 1. ч.т.д.

Замечание: для того, чтобы проверить сходимость-расходимость числового ряда его надо сравнить с заведомо сходящимся рядом *например бесконечно убывающей геометрической прогрессией) или заведомо расходящимся (например с грамоническим рядом или бесконечной программой с q>1)

41.

Признак Даламбера.

Пусть дан ряд åa_n (111) с положительными членами и существует

n=1

предел lim ((a_n+1)/(a_n))=r. Тогда:

n®¥

а) при r<1 ряд сходится; б) при r>1 ряд расходится.

Док-во: а) Пусть r<1 и lim ((a_n+1)/(a_n))=r. Докажем, что ряд (111)

n®¥

сходится. .По определению предела числовой последовательности для любого e>0 существует номер N такой, что при n³N выполняется неравенство ½(a_n+1)/(a_n) - r½< e. Отсюда следует, что r-e< (a_n+1)/(a_n)<r+e (1). Т. к. r<1, то e можно взять настолько малым, что будет выполнено неравенство r+e<1. Полагая r+e= q, на основании правого из неравенств (1) имеем (a_n+1)/(a_n)<q, или a_n+1 < a_nq для n=N, N+1, N+2… (2) Придавая n эти значения, из последнего неравенства получаем a_N+1<a_Nq, a_N+2<a_N+1q< a_Nq², a_N+3<a_N+2q< a_Nq³, …….., т.е. члены ряда a_N+1+a_N+2+ a_N+3+… меньше соответствующих членов ряда, составленного из элементов геометрической прогрессии: a_Nq+ a_Nq²+ a_Nq³+… (3). Так как q<1 , то ряд (3) сходится. Но ряд (2) получен из данного ряда (111 ) в результате отбрасывания конечного числа первых членов, след-но, по теореме о свойстве сходящихся рядов ряд (111) сходится.

б) Пусть теперь r>1. Докажем, что ряд (111) расходится. Возьмём e настолько малым, чтобы r-e<1. Тогда при n³N в силу левого из неравенств (1) выполняется неравенство (a_n+1)/(a_n)>1 или a_n+1> a_n. Таким образом, члены ряда , начиная с некоторого номера N , возрастают с увеличением их номеров, т.е. общий член ряда a_n не стремится к нулю при n®¥. Следовательно, по теореме о необходимом условии сходимости ряда, ряд (111) сходится.

Замечание. При r=1, как показывают примеры, ряд (111) может как сходиться, так и расходиться. В этом случае необходимо дополнительное исследование ряда с помощью др. признаков.

42. Интегральный признак Коши.¥

Пусть дан ряд f(1)+f(2)+f(3)+…+f(n)+…= åf(n)

n+1 (222) , члены которого являются значениями некоторой функции f(x , положительной, непрерывной и убывающей на +¥

полуинтервале [1, +¥). Тогда, если ò f(x)dx (333) сходится, то сходится и

1

ряд (222).Если же (333)расходится , то и ряд (222) также расходится.

Док-во: Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции y=f(x), с боковых сторон прямыми x=1, x=n, снизу осью Ох. Впишем в эту трапецию и опишем около нее две ступенчатые фигуры, состоящие из прямоугольников с основаниями [1,2], [2,3],…, [n-1,n] и высотами f(1), f(2), f(3),…, f(n-1), f(n). Тогда, принимая во внимание геометрический смысл определённого интеграла, имеем

n

f(2)+f(3)+…+f(n)<òf(x)dx (444)<f(1)+f(2)+…+f(n-1) , или, короче,

n 1

S_n-f(1)<òf(x)dx<S_n-f(n).

1 n n

Отсюда получаем: S_n<f(1) + òf(x)dx (1), S_n>f(n) + òf(x)dx (2) ,где S_n –

1 1

частичные суммы рассматриваемого ряда. Пусть интеграл (444) сходится. Это значит, что существует lim (444)=I.

n®¥ Так как f(x)>0, то последовательность (444) возрастает с увеличением n и ограничена сверху своим пределом: (444)<I. Из неравенства (1) следует , что S_n<f(1) + I, т.е. последовательность частичных сумм {S_n} ряда (222) ограничена. По теореме о необходимом и достаточном условиях сходимости ряда с неотрицательными членами ряд (222) сходится.

Пусть теперь интеграл (333) расходится. В этом случае (444)®+¥ при n®¥ (как монотонно возрастающая неограниченная последовательность). Из неравенства (2) следует, что S_n®+¥ при n®¥, т.е. последовательность частичных сумм {S_n} ряда (222) расходится и, следовательно, ряд расходится.

Степенные ряды.

¥

Ряд вида a₀ + a₁x +a₂x² +a₃x³+…+a_nxⁿ+…=åa_nxⁿ (1) называется степенным рядом.

n=0

Числа a₀, a_1, a_2,…,a_n,… называются коэффициентами степенного ряда.

Придавая х различные числовые значения , будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений х , при которых ряд (1) сходится, называется областью его сходимости. Это множество всегда не пусто, т.к. любой степенной ряд сходится при х=0. Очевидно, что частичная сумма S_n (х)= a₀ + a₁x +…+a_nxⁿ является функцией переменной х. Поэтому и сумма ряда S также является некоторой функцией переменной х, определённой в области

сходимости ряда:

¥ ¥

S=S(x)= åa_nxⁿ (или f(x)= åa_nxⁿ).

n=0 n=0

Теорема Абеля.

1) Если степенной ряд (1) сходится при х=х₀ (х₀¹ 0), то он сходится, и притом абсолютно, для всех х, удовлетворяющих условию я½ х½<½ х₀½.

2) Если ряд (1) расходится при х= х₁,то он расходится для всех х, удовлетворяющих условию ½х½<½х₁½.

¥

Док-во: 1)т.к. по условию числовой ряд åa_nx₀ⁿ сходится, то его общий член a_nx₀ⁿ ®0 при

n=0

n®¥, откуда следует, что последовательность { a_nx₀ⁿ } ограничена , т.е. существует число M>0 такое, что ½ a_nx₀ⁿ ½<M, n =0, 1, 2… (2) Перепишем ряд (1) в виде

a₀ + а₁х₀ (х/х₀) + а₂х²₀ (х/х₀)² +…+ а_n хⁿ₀ (х/х₀)ⁿ +… (3) и рассмотрим ряд, составленный из абсолютных величин его членов : ½a₀½+ ½а₁х₀½½х/х₀½ + ½а₂х²₀½½х/х₀½² +…+ ½а_n хⁿ₀½½х/х₀½ⁿ +… (4).

Члены ряда (4) в силу неравенства (2) меньше соответствующих членов ряда

М+ М½х/х₀½ + М½х/х₀½² +…+М½х/х₀½ⁿ +… (5) При ½ х½<½ х₀½ ряд (5) представляет собой геометрическую прогрессию со знаменателем q=½х/х₀½<1 и, следовательно, сходится.

Т.к. члены ряда (4) меньше соответствующих членов ряда (5) то, по признаку сравнения, ряд (4) также сходится, а это значит, что ряд (1) при ½ х½<½ х₀½ сходится абсоютно.

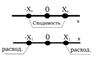По условию, в точке x₁ ряд (1) расходится. Требуется показать, что он расходится для всех x , удовлетворяющих условию ½ х½>½ х₁½. Предположим обратное, т.е. допустим, что при некотором значении х таком, что ½ х½>½ х₁½, ряд (1) сходится. Тогда по только что доказанной первой части теоремы ряд (1) должен сходиться и в точке х₁, т.к. ½ х₁½<½ х½. Но это противоречит тому, что в точке х₁ ряд расходится.

Теорема Абеля утверждает, что если х₀ – точка сходимости степенного ряда, то во всех точках, расположенных на интервале (-½х₀½,½ х₀½), этот ряд сходится абсолютно, а если х₁ – точка расходимости степенного ряда, то во всех точках, расположенных вне интервала (-½х₁½,½ х₁½), ряд расходится.

Понятие неопределенного интеграла.

Def Если функция F(x) является первообразной для функции f(x) на промежутке Х, то множество функций {F(x)+C}, где С- произвольная постоянная называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом òf(x)dx=F(x)+C. При этом f(x) называется подынтегральной функцией, f(x)dx- подынтегральным выражением, а переменная х- переменная интегрирования. òf(x)dx- выражает множество всех первообразных для функции f(x) на промежутке Х.

DefВосстановление функции по ее производной или что тоже самое: отыскание неопределенного интеграла называется интегрированием этой функции, т.к. F’(x)=f(x) òF’(x)dx=F(x)+C

Интегрирование- операция обратная дифференцированию и правильность интегрирования определяется следующим образом: мы должны продифференцировать результат и если получили подынтегральную функцию, то операция выполнена верно.

Основные свойства неопределенного интеграла:

1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. (òf(x)dx)’=f(x) и d( òf(x)dx)=f(x)dx Док-во: (òf(x)dx)’=(F(x)+C)’=F’(x)=f(x) и dòf(x)dx=(òf(x)dx)’dx=f(x)dx

2. d(òf(x)dx)=f(x)dx, дифференциал от неопределенного интеграла на промежутке Х равен подынтегральному вырожению.

Док-во: d(òf(x)dx)=d(F(x)+C)=(F(x)+C)’dx=F’(x)dx=f(x)dx

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. òdF(x)=F(x)+C. Док-во: т.к. òdF(x)=F’(x)dx, то по определению òF'(x)dx=F(x)+C

4. Постоянный множитель можно вынести из-под знака интеграла, т.е. если k=const¹0, то òkf(x)dx=kòf(x)dx. Док-во: пусть F(x) первообразная для f(x) на промежутке Х, т.е. "xÎX F’(x)=f(x)ÞkF(x) первообразная для kf(x), т.е. (kF(x))’=kF’(x)=kf(x). Из определения следует, что kòf(x)dx=k[F(x)+C]=kF(x)+C1=òkf(x)dx, где С1=кС, ч.т.д.

5. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно, т.е. ò(f(x)±g(x))dx=òf(x)dx±òg(x)dx. Док-во: пусть F(x) и G(x) являются первообразными для функций f(x) и g(x) на промежутке Х, т.е. "хÎХ F’(x)=f(x), G'(x)=g(x). Тогда функции F(x)±G(x) являются первообразными для функция f(x)±g(x). Следовательно, òf(x)dx±òg(x)dx=(F(x)+C1)±(G(x)+C2)=(F(x)±G(x))+(C1±C2)=[F(x)±G(x)]+C=ò(f(x)±g(x))dx

Это свойство справедливо для любого конечного числа слагаемых.

Методы замены переменной

1. Непосредственное интегрирование.

С помощью табл осн интегралов.

2. Метод подстановки или метод замены переменных.

Достаточно часто введение новой переменой позволяет свести интеграл к табличному

[Т] Пусть функция х=j(t) определена и дифференцируема на некотором промежутке Т и пусть Х- множество значений этой функции, на котором определена функция y=f(x), т.е. на T определена сложная функция y=f[j(t)]. Тогда если на множестве Х функция f(x) имеет первообразную F(x), то справедлива формула òf(x)dx|_x=j(t)= òf[j(t)]j’(t)dt. Док-во: Пусть функция F(x) является первообразной для функции f(x) на множестве Х. Рассмотрим на множестве T сложную функцию F[j(t)]. Продифференцируем ее по правилам дифференцирования сложной функции: F’[j(t)]*j’(t)=f’[j(t)]*j’(t)Þ мы получили что эта функция имеет на множестве Т первообразную F[j(t)]. òf[j(t)]*j’(t)dt=F[j(t)]+C=F(x)+C|_x=j(t)= òf(x)dx|_x=j(t). Получили искомую формулу замены переменных в неопределенном интеграле.

Замечание: При замене переменныхв неопределенном интеграле иногда более удобно задавать не х как функцию t, а задавать t как функцию от х.