Линейная зависимость векторов.

РАЗЛОЖЕНИЕ ВЕКТОРА ПО СИСТЕМЕ ВЕКТОРОВ.

РАНГ МАТРИЦЫ

Вопросы

1. Определение однородной системы линейных алгебраических уравнений.

2. Когда однородная система имеет единственное решение.

3. Что называется линейной комбинацией системы векторов.

4. Какая линейная комбинация векторов называется нулевой.

5. Когда вектор 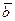разлагается по системе векторов .

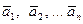6. Когда система векторов будет линейно зависимой.

7. Когда система векторов будет линейно независимой.

8. Что такое ранг матрицы.

9. Как найти ранг матрицы.

10. Чему равен ранг транспонированной матрицы.

11. Теорема Кронекера-Капелли.

12. Ранг произведения матриц.

СЛАУ называется однородной, если все ее свободные члены равны 0.

……….

.

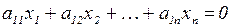
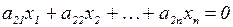
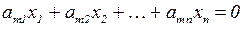Однородная СЛАУ имеет единственное решение, когда ее определитель не равен 0.

.

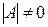Линейной комбинацией системы векторов 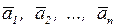с коэффициентами 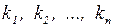называется выражение:

.

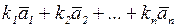Например: линейная комбинация векторов 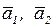с коэффициентами 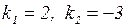имеет вид:

.

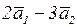Линейная комбинация называется нулевой,если в результате получается нуль-вектор :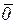

.

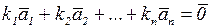Вектор 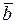разлагается по системе векторов 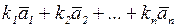, если он может быть представлен в виде линейной комбинации этих векторов, то есть: .

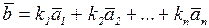Система векторов 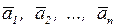называетсялинейно зависимой,если найдутся такие коэффициенты 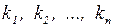, не все равные нулю одновременно, такие, что линейная комбинация данных векторов с этими коэффициентами будет нулевой:

.

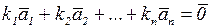Система векторов 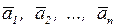называетсялинейно независимой,если нулевая линейная комбинация этих векторов возможна только при равных нулю коэффициентах, то есть:

.

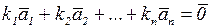
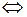
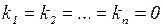Ранг матрицы –это максимальное число ее линейно независимых строк (или столбцов). Чтобы найти ранг матрицы надо привести ее к ступенчатому виду.

Матрица ступенчатого вида выглядит так:

Темным цветом помечены угловые элементы – числа, не равные 0.

Правее и выше угловых элементов – любые числа.

Левее и ниже угловых элементов – нулевые элементы.

При приведении матрицы к ступенчатому виду используют элементарные преобразования I и II типа над строками матрицы.

Количество угловых элементов матрицы равно рангу этой матрицы.

Ранг матрицы А равен рангу транспонированной матрицы .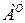

Теоре́ма Кро́некера –Капе́лли – критерий совместности системы линейных алгебраических уравнений:

СЛАУ совместна (имеет решения) тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Ранг произведения двух матриц А и В не выше ранга каждого из сомножителей: .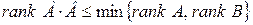

ВЕКТОРЫ В ПРОСТРАНСТВЕ. ОПЕРАЦИИ НАД ВЕКТОРАМИ

Вопросы

1. Что такое геометрический вектор.

2. Что называется модулем вектора.

3. Какой геометрический вектор называется нулевым (его длина и направление).

4. Когда равны два геометрических вектора.

5. Что такое свободный вектор.

6. Как найти сумму нескольких геометрических векторов.

7. Как сложить два вектора по правилу параллелограмма.

8. Как определяется вектор 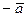, противоположный к вектору .

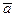9. Как найти разность векторов 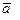и .

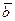10. Как определяется вектор 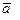, умноженный на скаляр k.

11. Свойства векторного сложения и умножения вектора на скаляр.

12. Какие два вектора называются коллинеарными. Основное свойство коллинеарных векторов.

13. Как выглядит условие коллинеарности векторов.

14. Какие три вектора называются компланарными.

15. Как выглядит условие компланарности векторов.

16. Как найти длину (модуль) вектора в .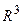

17. Как найти координаты вектора, зная координаты его начала и конца.

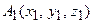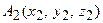18. Как найти расстояние между точками и в .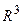

19. Что называется скалярным произведением векторов в .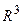

20. Свойства скалярного произведения.

21. Какие векторы называются ортогональными.

22. Чему равно скалярное произведение ортогональных векторов.

23. Как выглядит условие ортогональности векторов.

Вектором в пространстве 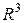называется направленный отрезок. Направление вектора обозначается стрелкой.

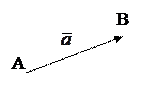Вектор .

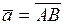Длиной вектора называется длина отрезка.

Нулевым вектором называется вектор, длина которого равна 0. Считается, что направление нулевого вектора произвольно.

Два вектора равны, если они имеют одинаковую длину и направление.

Свободный вектор, это вектор, который можно перемещать в пространстве без изменения длины и направления.

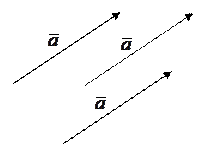
Вектор, противоположный к вектору 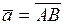, это вектор 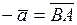, имеющий туже длину и направленный в противоположную сторону.

Суммой нескольких векторов называется вектор по длине и направлению равный замыкающему пространственной ломаной построенной на этих векторах (рис.1)

Рис 1.

Сумма двух векторов 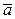и 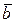может быть найдена по правилу параллелограмма:

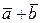– это диагональ параллелограмма, построенного на этих векторах, выходящая из общей точки их приложения (рис.2).

Рис 2.

Разностью векторов 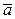и 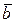называется вектор 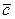, такой что 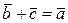(рис.3)

Рис 3.

При умножении вектора 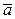на скаляр k получается вектор 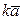, длина которого равна 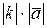, а направление совпадает с направлением вектора 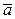, если 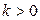и противоположно направлению вектора 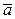, если 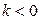. Если 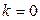, направление 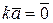произвольно.