Тема. 4.3 Основы математической статистики.

Студент должен:

знать: - методы исследования статистических данных;

-определение эмпирической функции;

-генеральные и выборочные совокупности; оценки параметров;

- несмещенные и состоятельные оценки;

- точность оценки и доверительные интервалы.

уметь: - составлять эмпирическую функцию и строить ее график;

- определять смещенную и нормальную оценки;

-определять точность оценки;

- определять доверительные интервалы.

Выборочный метод исследования статистических данных, эмпирическая функция распределения. Генеральная и выборочная совокупности. Несмещенные эффективные и состоятельные оценки параметров. Генеральная средняя, выборочная средняя. Оценка генеральной средней по выборочной средней. Генеральная дисперсия, генеральное среднее квадратичное отклонение. Оценка генеральной дисперсии по исправленной выборочной. Точность оценки, доверительная вероятность, доверительный интервал. Доверительные интервалы для параметров нормально распределенной генеральной совокупности.

Методические указания.

Цель математической статистики состоит в указании методов сбора и группировки статистических сведений, которые получены в результате экспериментов или наблюдений. Вторая задача- это разработка методов анализа статистических данных: оценки вероятности события, а также функций и параметров распределения; оценка зависимости случайной величины от других случайных величин; проверка статистических гипотез о виде и виде величинах параметров неизвестного распределения.

Вопросы для самоконтроля.

1. Дайте определение генеральной и выборочной совокупности.

2. Укажите способы отбора.

3. Дайте определение статистического распределения выборки и его характеристики

4. Что называют эмпирической функцией распределения?

5. Как строится график эмпирической функции?

6. Что называют полигоном и гистограммой?

7. Какие виды статистических оценок вы знаете?

8. Что такое доверительный интервал?

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

Номер темы	Номер и наименование работы	Количество аудиторных часов
1.1 1.2	Вычисление матричного многочлена. Решение систем линейных уравнений методом Крамера.
	Действия над комплексными числами в алгебраической, тригонометрической и показательных формах
3.1 3.2 3.3	Производная сложной функции. Исследование функции и построение графика
4.1 4.2 4.3	Решение простейших задач на определение вероятности. Нахождение математического ожидания и дисперсии случайной величины по заданному закону распределения

ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

ОБЩИЕ ТРЕБОВАНИЯ

Требования к выполнению и оформлению контрольной работы.

1. Работа выполняется в отдельной тетради школьного формата. Следует пронумеровать страницы и оставить на них поля не менее 3 см для замечаний преподавателя.

2. На обложке тетради должен быть приклеен титульный лист утвержденного образца и аккуратно записаны все данные: шифр, Ф. И. О. студента, предмет и номер работы.

3. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво.

4. Решение задачи располагайте в порядке номеров, указанных в задании, номера задач следует указывать перед условием.

5. Условия задач должны быть обязательно переписаны полностью в контрольную тетрадь.

6. При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения. Перечислим важнейшие из этих требований:

- студенты должны соблюдать абзацы, всякую новую мысль следует начинать с новой строки;

- важные формулы равенства, определения нужно выделять в отдельные строки;

- при описании решения задачи краткая запись условия отделяется от решения и в конце решения ставится ответ;

- серьезное внимание следует уделять правильному написанию сокращенных единиц измерения;

- необходимо правильно употреблять математические символы.

7. Решения задач должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.

8. Чертежи следует выполнять карандашом с использованием чертежных инструментов, соблюдая масштаб.

9. В конце работы следует указать литературу, которой вы пользовались, проставить дату выполнения работы и подпись.

10. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки.

Контрольные работы должны быть выполнены в срок (в соответствии с учебным планом - графиком). В период сессии работы на проверку не принимаются. Если в работе допущены недочеты и ошибки, то студент должен выполнить все указания преподавателя, сделанные в рецензии.

Студенты, не имеющие зачет по контрольной работе, к экзамену не допускаются. Во время экзамена зачтенные контрольные работы предоставляются преподавателю.

Контрольная работа имеет 30 вариантов. Вариант работы выбирается согласно двум последним цифрам шифра студента.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

К решению первой задачи контрольной работы следует приступить после изучения темы «Матрицы и определители».

Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов:

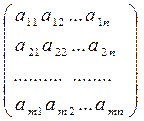
Сокращенно можно записать 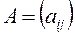, где

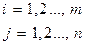
Любой элемент -это элемент, находящейся на пересечении 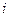-той строки и 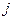-того столбца.

Если количество строк n не равно количеству столбцов m, то матрицу называют прямоугольной.

Пример.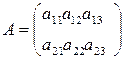

Если количество строк n равно количеству столбцов m, то матрицу называют квадратной.

Пример. .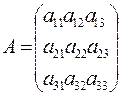

Число строк и столбцов квадратной матрицы называют порядком квадратной матрицы.

Рассмотрим квадратную матрицу порядка n: 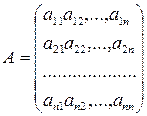.Диагональ, содержащая элементы 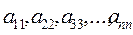- главная диагональ, диагональ содержащая 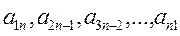-побочная диагональ.

Матрица вида 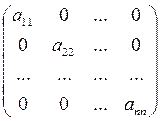называется диагональной.

Пример. .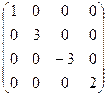

Если у диагональной матрицы все числа равны, то есть 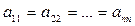, то матрица называется скалярной. Скалярную матрицу, у которой все числа главной диагонали равны единице, называют единичной и обозначают E.

Пример. .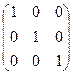

Матрицу, у которой все элементы равны 0, называют нулевой матрицей и обозначают 0=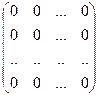

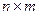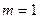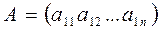В прямоугольной матрице типа , если , то - матрица- строка.

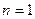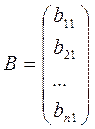Если , то -матрица- столбец

Матрицы-строки и матрицы-столбцы иначе называются векторами.

Две матрицы называются равными, если у них одинаковое число строк m и одинаковое число столбцов n и их соответствующие элементы равны: .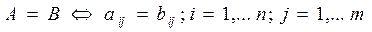

Пример: .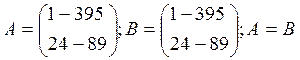

Пусть дана матрица размерности 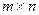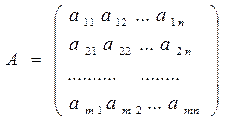.Переставляя строки со столбцами, получаем матрицу размерности 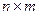, которую называют транспонированной и обозначают .

.

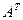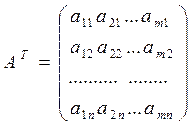Операции над матрицами.

1. Сложение (вычитание) матриц одинаковых размерностей.

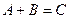. Чтобы найти сумму (разность) двух (и более) матриц с одинаковым числом строк и столбцов необходимо сложить (вычесть) соответствующие элементы.

Пример. ; .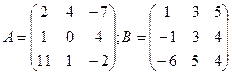

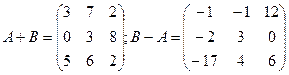Так как сложение матриц сводится к сложению чисел, то данная операция обладает теми же свойствами, что и сложение чисел, а именно:

1. .

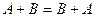2.

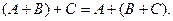
3.

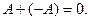
2. Умножение матрицы на число 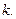Каждый элемент матрицы умножаем на число

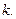
Пример. .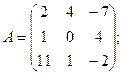

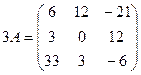Свойства:1.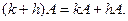

2. .

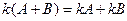3.

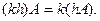
3. Умножение матриц. Матрицы можно перемножить тогда, когда число столбцов матрицы равно числу строк матрицы 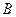. Чтобы найти элемент стоящий на 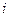-той строке и 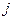-том столбце матрицы 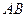, нужно умножить соответствующие элементы 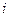строки и 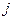столбца и сложить произведения.

Пример.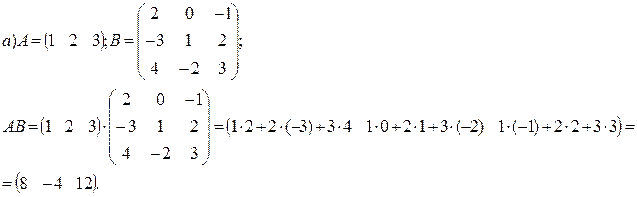

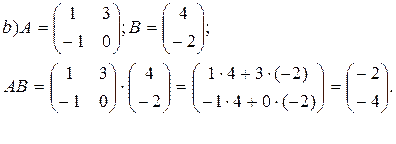
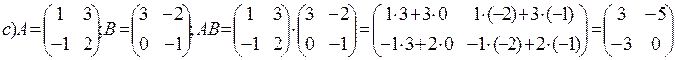
Свойства:

1. .

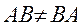2. .

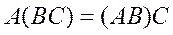3. .

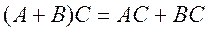Для квадратичных матриц возможно составление многочленов. Многочлен степени 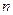от квадратичной матрицы называется выражение

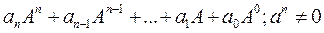или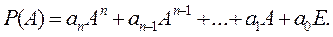

Если 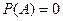, то матрица называется корнем многочлена 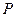, сам многочлен называется аккумулирующим для матрицы .

Пример. Найти значение матричного многочлена ( ):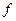

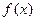=-x³+3x²+x-2, = .

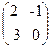Решение. В многочлен 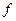вместо 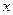подставляем матрицу и в ответе получаем матрицу той же размерности, что и матрица .

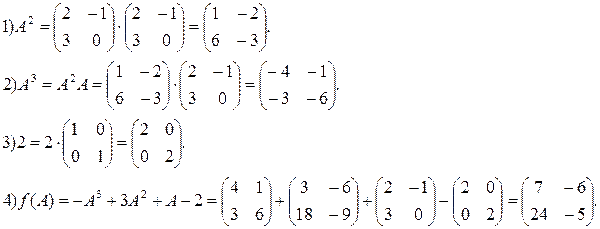
Пусть дана квадратная матрица второго порядка.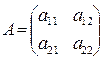

Определителем (детерминантом) второго порядка, соответствующей данной матрице, называется число равное разности произведений элементов главной и побочной диагонали. Обозначение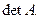

.

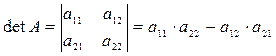Пример. Вычислить .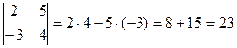

Рассмотрим квадратную матрицу третьего порядка .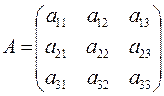

Определитель (детерминант) третьего порядка вычисляется по формуле:

.

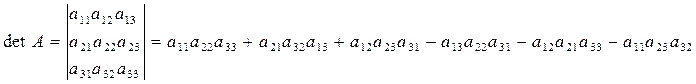Пример. Вычислить

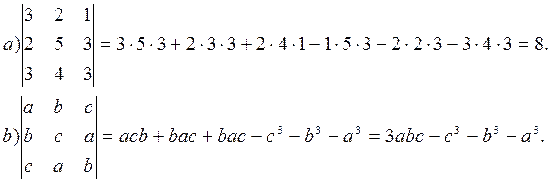
Свойства определителей.

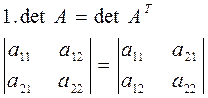
2. При перестановке двух строк или столбцов определитель изменить свой знак на противоположный.

3. Общий множитель всех элементов строки или столбца можно вынести за знак определителя.

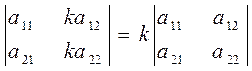
4. Определитель с двумя одинаковыми строками или столбцами равен нулю. Пример. .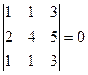

5. Определитель, у которого все элементы двух строк или двух столбцов пропорциональны, равен нулю. Пример.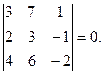

6. Если к какой-либо строке или столбцу определителя прибавить элементы другой строки или столбца, умноженные на одно и то же число, то определитель не изменит своей величины.

.

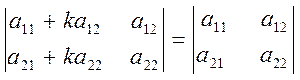7. Треугольный определитель, у которого все элементы лежащие выше или ниже главной диагонали- нули, равен произведению элементов главной диагонали.

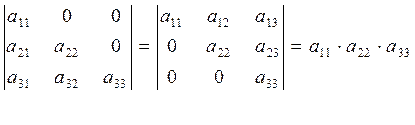
Свойства 6 и 7 дают еще один способ вычисления определителей: приводим определитель к треугольному виду, пользуясь свойством 6 ,и вычисляем его значение, опираясь на свойство 7.

Пример.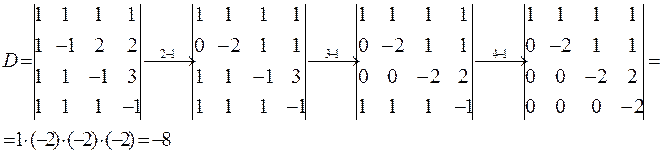

Рассмотрим определитель .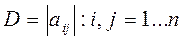

Минором 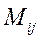элемента 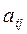определителя 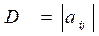называется новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих данный элемент.

Пример. 1)Минор элемента 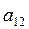будет .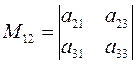

2)Выпишем все миноры определителя третьего порядка .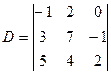

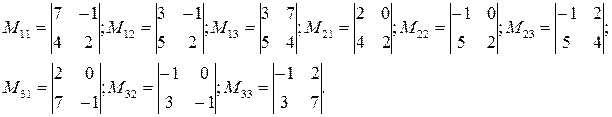
Алгебраическим дополнением элемента 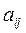определителя 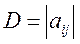называется минор 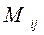этого элемента, взятый со знаком 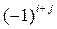, и обозначается . .

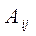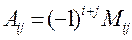Пример.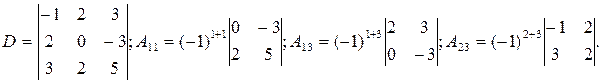

Сумма произведений элементов любой строки или столбца определителя 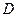на их алгебраические дополнения равна этому определителю.

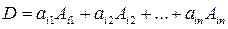- разложение определителя по элементам 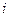-той строки. 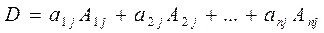- разложение определителя по элементам 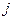-того столбца.

Пример. 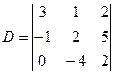. Найдем значение этого определителя разложением по первому столбцу.

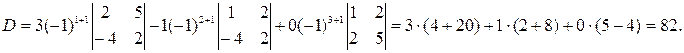
Таким образом – это третий способ вычисления значений определителей, который позволяет найти значение определителей более высоких порядков.

Пример.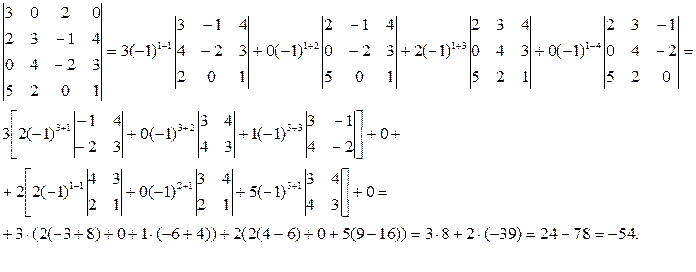

К решению второгозадания приступить после изучения темы «Системы линейных уравнений».

Пусть дана система m линейных уравнений с n неизвестными

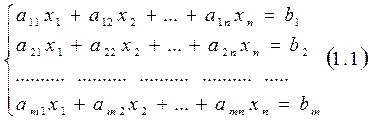
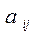-коэффициенты системы, 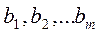- свободные члены.

Если 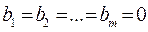, то система называется однородной, иначе неоднородной.

Матрица , составленная из коэффициентов системы (1.1) 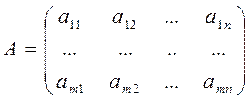-называется матрицей системы (1.1) или основной матрицей.

Определитель 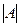- определитель исходной системы уравнений (1.1).

Расширенной матрицейлинейной системы (1.1) называется матрица, которая получается из основной прибавлением столбца свободных членов:

.

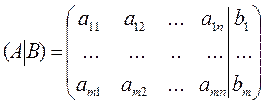Решением системы (1.1) называется совокупность чисел 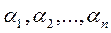, обращающих все уравнения системы в тождество.

Если система линейных уравнений не имеет решения, то она называется несовместной. Если система имеет хотя бы одно решение, то она называется совместной.

Две системы называются эквивалентными, если множество их решений совпадают.

1.Матричный способ.

Если ввести обозначение

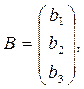
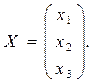
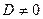то исходную систему можно записать в виде -это матричное уравнение. Такое уравнение решается следующим образом. Пусть матрица невырожденная ( ), тогда существует обратная матрица 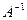. Умножив на нее обе части матричного уравнения, имеем .
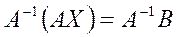Используя сочетательный закон умножения, перепишем это равенство в виде 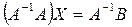. Поскольку 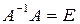и 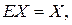, находим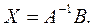

Таким образом, чтобы решить систему матричным способом, нужно:
1. Записать систему в виде матричного уравнения и решить ее. Найти обратную матрицу .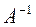
2.Найти произведение обратной матрицы 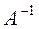на матрицу-столбец свободных членов 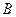, т. е.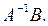
3. Пользуясь определением равных матриц, записать ответ.
Пример 1. Решим систему уравнений 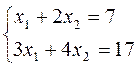. Запишем систему в виде матричного уравнения 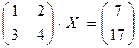. Для этого будем искать обратную матрицу 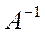. Найдем определитель матрицы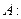

.

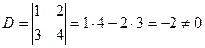Вычислим алгебраические дополнения каждого элемента матрицы :

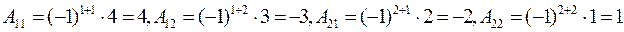
Запишем матрицу 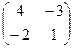и транспонируем ее: 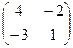. Учитывая, что 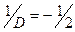, запишем обратную матрицу .

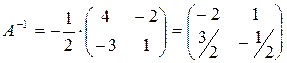2.Умножим матрицу 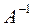на матрицу :

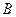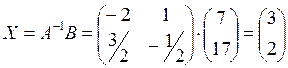
3. Так как 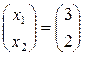, то по определению равных матриц получим .

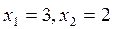Метод Крамера.

Рассмотрим систему n линейных уравнений с n неизвестными
.

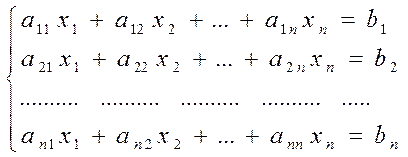Составим определитель исходной матрицы .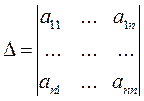

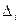-определитель, полученный из определителя 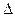заменой 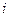-го столбца из коэффициентов при неизвестном 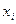на столбец свободных членов, то есть , , …, .

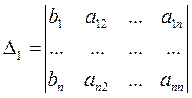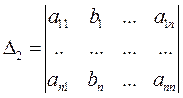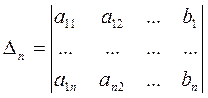Если 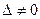, то система имеет единственное решение и по формулам Крамера 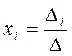, где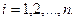

Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта:

1. 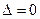и каждый определитель 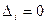. Это имеет место только тогда, когда коэффициенты при неизвестных 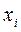пропорциональны, т.е. каждое уравнение системы получается из первого уравнения умножением обоих его частей на число 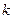. Очевидно, что при этом система имеет бесчисленное множество решений.

2. 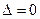и хотя бы один из определителей 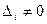. Это имеет место только тогда, когда коэффициенты при всех неизвестных, кроме 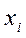, пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решений.

Пример 2. Решим систему, применяя метод Крамера .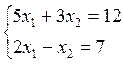

Вычислим определитель системы 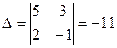. Вычислим определители 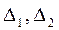: 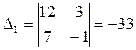; 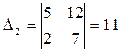. Найдем значения 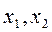по формулам Крамера: 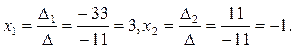Итак, решение системы есть (3;-1).

Метод Гаусса.

При решении систем линейных уравнений используют также метод Гаусса (метод последовательного исключения неизвестных). Он состоит в следующем: систему приводят к эквивалентной ей системе с треугольной матрицей или к ступенчатому виду. Эти действия называют прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).

При выполнении прямого хода используют следующие преобразования:

1) умножение или деление коэффициентов свободных членов на одно и то же число;

2) сложение и вычитание уравнений;

3) перестановку уравнений системы;

4) исключение из системы уравнений, в которых все коэффициентов при неизвестных и свободные члены равны нулю.

Пример 3. Используя метод Гаусса, решим систему уравнений .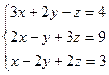

Решение. Запишем расширенную матрицу 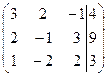. Переставим третью и первую строки местами: 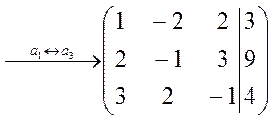. Чтобы в 1-м столбце получить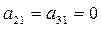 , умножим 1-ю строку сначала на 3, а затем на 2 и вычтем результаты из 2-ой и 3-й строк: 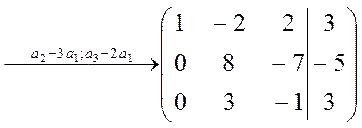. Разделим 2-ю строку на 8, полученную результаты умножим на 3 и вычтем из 3-й строки:. 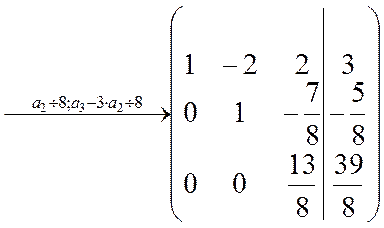Разделим 3-ю строку на :.

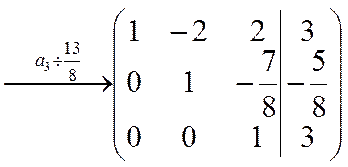Выполняя обратный ход, с помощью последовательных подстановок находим неизвестные: 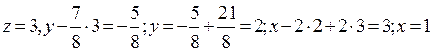. Итак, получаем ответ(1;2;3).

К решению третьего задания приступайте после изучения темы «Основы теории комплексных чисел».

Комплексным числом называется число вида 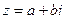, где 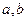- действительные числа, а число 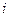, определяемое равенством 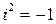, называется мнимой единицей.

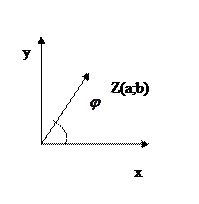
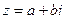, можно рассмотреть как вектор 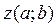. Ось oy-мнимая, ось ox- действительная.

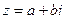- алгебраическая форма комплексного числа.

Действия над комплексными числами в алгебраической форме

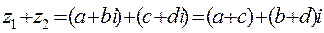
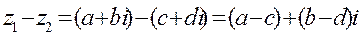
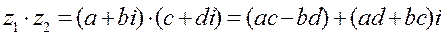
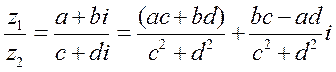
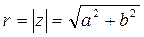-модуль комплексного числа

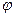- угол, образованный между вектором 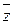и положительным направлением оси ox- аргумент

Аргумент определяем по формулам 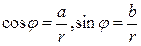( угол будет со знаком «+», если он берется против часовой стрелки, и со знаком «-», если по часовой стрелке). Иногда угол легко определяется по рисунку.

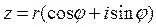-тригонометрическая форма.

Правило перехода от алгебраической формы к тригонометрической форме:

Находят модуль комплексного числа 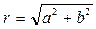. Для нахождении аргумента 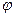сначала определяют геометрически, в какой четверти находится точка z. Составляют уравнения 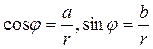и по решению одного из них находят угол 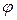. Записывают комплексное число в тригонометрической форме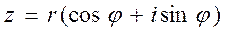

Действия над комплексными числами в тригонометрической форме

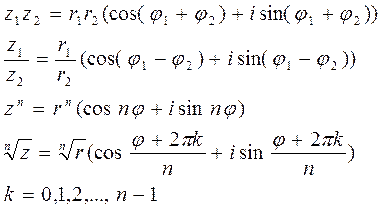
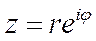- показательная форма комплексного числа.

Действия над комплексными числами в показательной форме

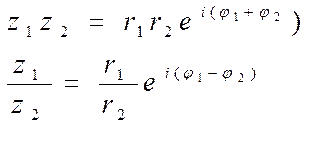
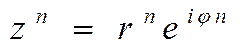
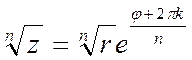, где k принимает n значений: 0, 1, 2, …, n-1.

Пример. 1)Выполните действия: 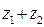, , 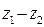, , 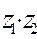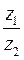где

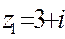
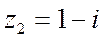
Решение.

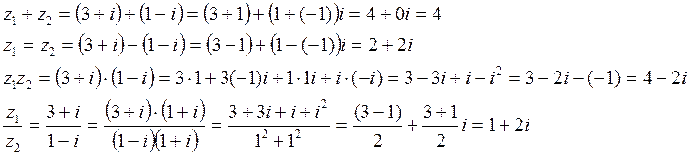
2) Возведите в степень .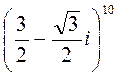

Решение. Сначала переведем комплексное число в тригонометрическую форму.

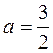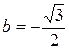, . Модуль 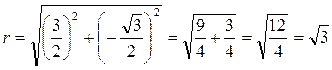,точка изображающее данное число, лежит в 4 четверти и 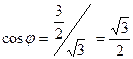, поэтому .

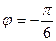Следовательно 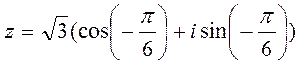. 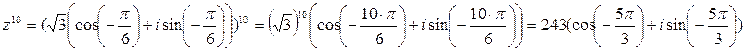3) Извлеките корень .

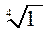Решение. Для начала представим число в тригонометрической форме: 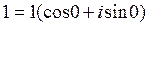Воспользуемся формулой .

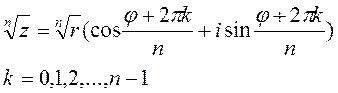В нашем случаи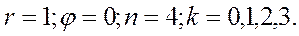

Получаем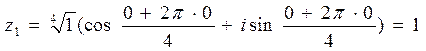

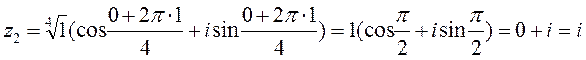
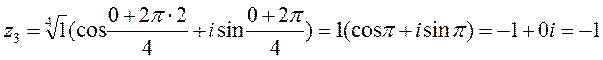
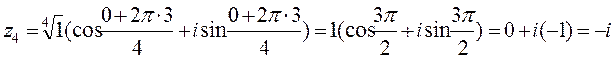
К решению четвертогозадания нужно приступить после изучения темы «Функции, пределы, непрерывность».

ОБЩИЙ ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИЙ

И ПОСТРОЕНИЯ ГРАФИКОВОВ

Под «исследованием функции» обычно понимается разыскание:

1. области определения функции, выявление четности и нечетности, периодичности функции; точек пересечения с координатными осями;

2. точек разрыва функции;

3. асимптот графика (если требуется, то дополнительно исследовать поведение функции при )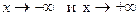

4. интервалов возрастания и убывания;

5. точек максимума и минимума, а также экстремальных значений;

6. областей выпуклости вверх (вниз) графика функции, точек перегиба.

На основании проведенного исследования строится график функции.

Пример. Построить график функции .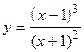

1) Область определения функции: 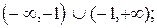пересечение оси 0х в точке (1;0), а оси 0у - (0;-1);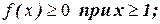

2) 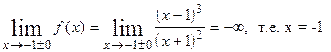точка разрыва;

3) из 2) 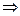х=-1 вертикальная асимптота;

Находим наклонную асимптоту:

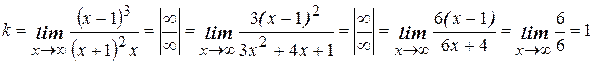
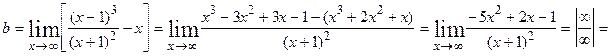
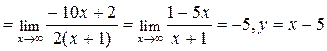- наклонная асимптота при

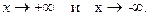
4) =

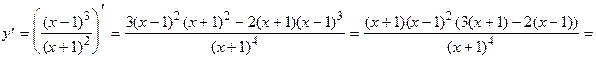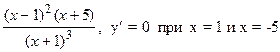
при 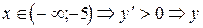(возрастает)

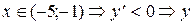(убывает)

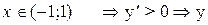(возрастает)

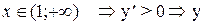(возрастает)

5) Из предыдущего 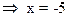точка максимума,

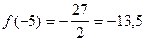- max;

6)

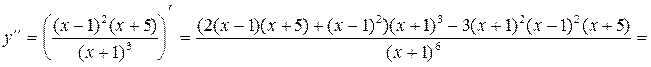
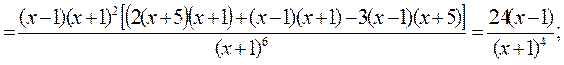
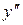=0 при х=1;

При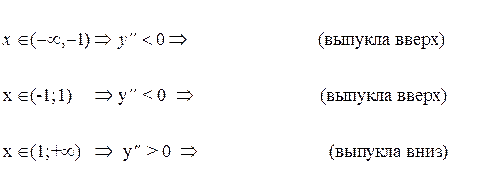

х=1 абсцисса точки перегиба, у (1)=0.

Результаты исследования внесем в следующую таблицу

х		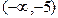-5	(-5;-1)	(-1;1)		(1;+4)
	+		-	+		+
	-	-	-	-		+
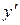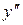y		-27/2- max

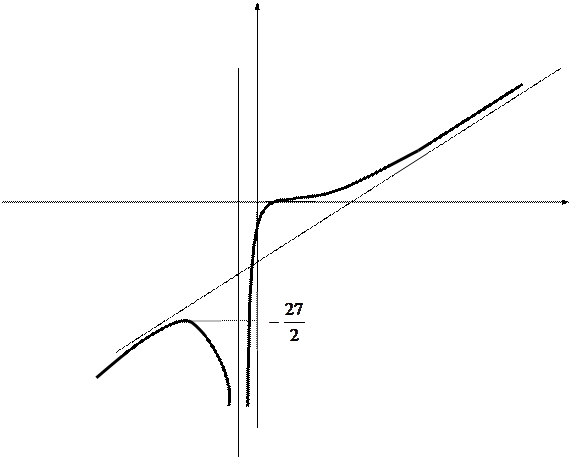
К решению пятого заданияконтрольной работы следует приступить после изучения темы "Дифференциальное и интегральное исчисление" (Производная функции).

Предел отношения приращения функции D у к вызвавшему его приращению аргументу D х при стремлении D х к нулю, то есть 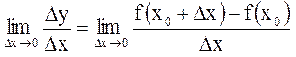называется производной функции у = f (х) по аргументу х в точке х0.

Производная обозначается одним из символов: у', f ' (х), 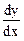, а ее значение при х = х0 обозначается у' (х0), f ' (х0) , .

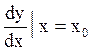Операция нахождения производной называется дифференцированием, сама функция называется дифференцируемой, если имеет конечную производную.

Производная сложной функции.

Если у = f (и), и = 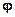(х) - дифференцируемые функции своих аргументов, то производная сложной функции у = f( 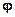(х)) существует и равна произведению производной функции у по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной х:

ух' = уu'.их'

Эта формула распространяется и на сложные функции, которые задаются с помощью цепочки, содержащей три звена и более.

Правила дифференцирования

Во всех приведенных формулах буквами U;V обозначены дифференцируемые функции независимой переменной х: U= U(х), V= V(х), а буквами а, C, n - постоянные.

1. с' = 0 4. (UV)’=U’V+UV’

2. х' = 1 5. (CU)' = CU'

3. (U+V)' = U’ +V ' 6.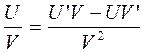

Формулы дифференцирования

Основные элементарные Сложные формулы

формулы

7. 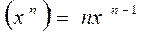7a.

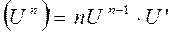
8. 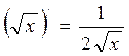8а.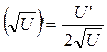

9. (sin x)' = cos x 9а. (sin U)'= cos U . U'

10. (cos x)' = - sin x 10а. (cos U)'= - sin U . U'

11. 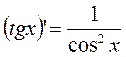11а.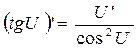

12. 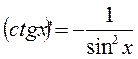12а.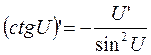

13. 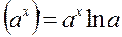13а.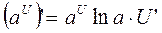

14. 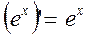14а.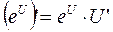

15. 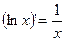15а.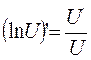

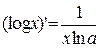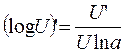16. 16а . где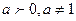

17. 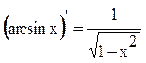17а.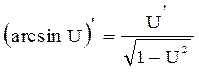

18. 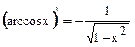18а.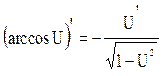

19. 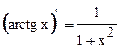19а.

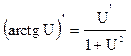
20. 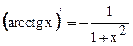20а.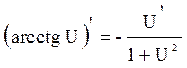

Пример 1

Найдите производную функции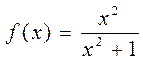

Решение

Применяя правила 6, 3, 1 и формулу 7 получим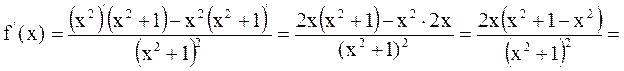

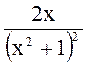
Пример 2

Найдите производную функции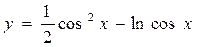

Решение

Это сложная функция с промежуточным аргументом cos х. Применяя правила 3,5 и формулы 7а, 10, 15а, получим :