Решение многокритериальной задачи управления

В общем виде многокритериальная задача оптимального управления, именуемая также векторной задачей математического программирования, формулируется следующим образом: для системы, описываемой векторным дифференциальным уравнением

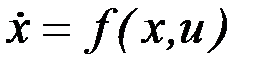(6.41)

с начальным условием

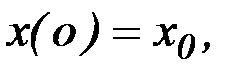(6.42)

определить на отрезке времени 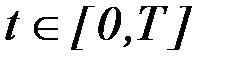вектор управления 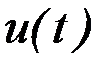, на который наложены ограничения

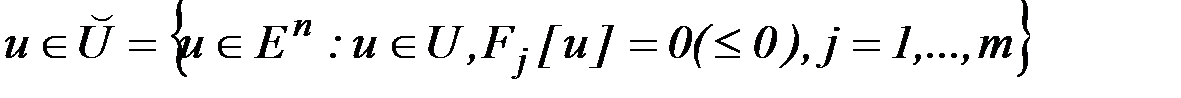, (6.43)

из условия минимума векторного критерия

.

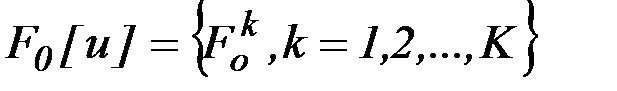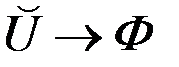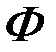В этой задаче задается отображение , где - область допустимых значений критериев, образуемая допустимыми значениями векторов 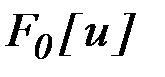при управлениях, удовлетворяющих условиям (6.43).

Решением многокритериальной задачи может быть только компромиссное решение, удовлетворяющее в том или ином смысле всем компонентам векторного критерия .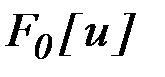

В качестве опорного множества для выбора единственного решения многокритериальной задачи может служить множество неулучшаемых по Парето ( 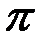-оптимальных) управлений 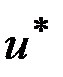, принадлежащих множеству 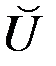. Это множество является неулучшаемым в том смысле, что для каждой точки (управляющей зависимости) 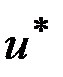этого множества не существует другой допустимой точки (управляющей зависимости) 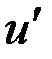, для которой

, ,

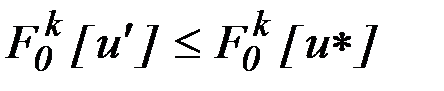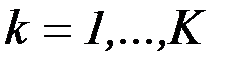причем хотя бы для одного критерия должно выполняться строгое неравенство.

Получение единственного решения многокритериальной задачи, имеющей множество решений как множество Парето, возможно путем сведения задачи к однокритериальной или к заранее определенной последовательности однокритериальных задач.

1. Методы, основанные на свертывании критериев.

Задача легко сводится к однокритериальной, если удается обосновать введение весовых коэффициентов 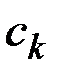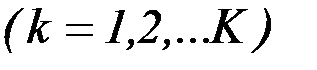, характеризующих относительную важность соответствующих им критериев. Весовые коэффициенты обычно нормируются, составляя в сумме единицу. Однокритериальная задача формирования управления в этом случае формулируется следующим образом. Определить управление 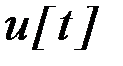для системы (6.41) с начальным условием (6.42), удовлетворяющее ограничениям (6.43) и минимизирующее функционал

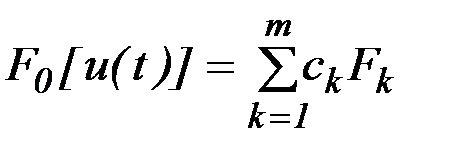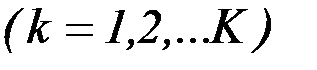, . (6.44)

Основным достоинством методов, основанных на свертывании критериев в соответствии с (6.44), является выполнение условий оптимальности по Парето. К недостаткам рассматриваемого подхода относится то, что обычно известна лишь сопоставимая важность критериев, но трудно априори найти численные значения весовых коэффициентов, удовлетворяющие всем возможным ситуациям. Кроме того, в ряде случаев малым приращениям весовых коэффициентов соответствуют большие приращения целевых функций и полученное решение является неустойчивым.

2. Методы, использующие ограничения на критерии.

Автоматизировать поиск единственного решения многокритериальной задачи позволяет метод последовательных уступок. В этом случае критерии располагаются и нумеруются в порядке убывания важности. Затем производится последовательная оптимизация критериев, начиная с первого, при условии наличия возможности некоторого ухудшения предыдущих критериев (допустимой уступки). После оптимизации последнего по важности критерия при условии выполнения заданных ограничений на все критерии решение задачи считается найденным.

К недостаткам методов, построенных на последовательных уступках, относится то, что, во-первых, полученное решение в общем случае не оптимально по Парето, а, во-вторых, затруднительно априорное на все возможные случаи назначение величин уступок, которые, как правило, несоизмеримы между собой.

3. Методы целевого программирования.

Эти методы предполагают наличие определенной цели по каждому из критериев. Величины целей используются при преобразовании исходной задачи в задачу целевого программирования, которая представляется как минимизация некоторой суммы отклонений с нормированными весами.

Основными недостатками методов целевого программирования являются несоизмеримость разностей критериев и величин соответствующих целей, а также трудности с выбором весов.

4. Методы, основанные на отыскании компромиссного решения.

Эти методы обеспечивают гарантированный результат решения задачи управления из условия поиска максимума минимального (максимин) или минимума максимального (минимакс) критерия.

Распространенным подходом, позволяющим выбрать единственное решение задачи управления, является сведение рассматриваемой задачи к минимаксной: найти управление 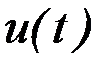для системы (6.41) с начальным условием (6.42), удовлетворяющее ограничениям (6.43) и доставляющее минимум функционалу

,

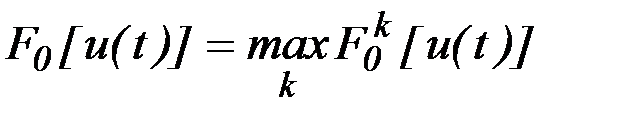
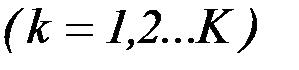т.е. найти

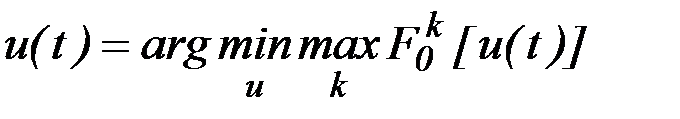
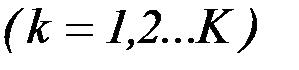(6.45)

при условии выполнения ограничений (6.43).

При решении минимаксной задачи функционалы 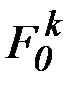сравниваются по величине, и поэтому численному решению этой задачи предшествует операция нормализации функционалов.

Существование решения минимаксной задачи (6.45), удовлетворяющего ограничениям (6.43), гарантирует существование решения поставленной задачи управления и притом единственного. Управление, являющееся решением минимаксной задачи, сформулированной соответствующим образом, по сравнению с другими управлениями гарантирует, в частности, наибольшее удаление наихудшего из функционалов от границы области допустимых значений.

Рассмотрим подход, основанный на отыскании компромиссного решения (гарантированного результата) в виде (6.45).

Пусть известны диапазоны изменения 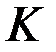критериев задачи

,

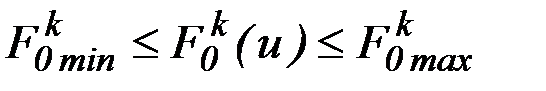
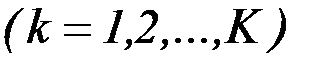где 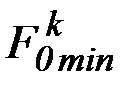- минимальное значение 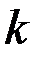-го критерия, полученное в результате решения однокритериальной задачи оптимизации без учета остальных критериев и достигаемое при управлении 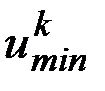, 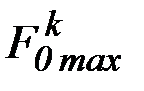- максимальное значение 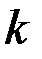-го критерия среди значений, соответствующих управлениям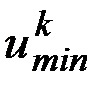 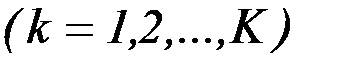. В этом случае обоснована нормализация

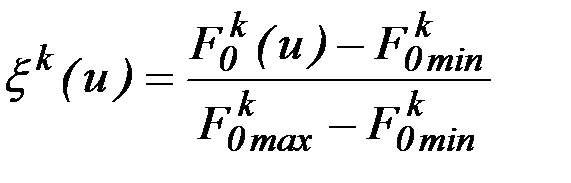
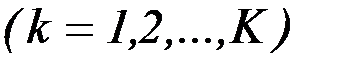, (6.46)

при которой 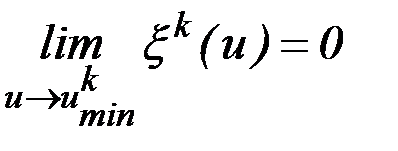, 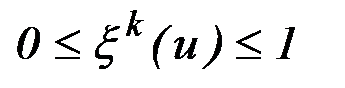. Значения 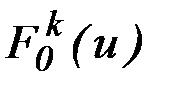вычисляются для текущего приближения искомого управления .

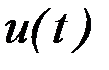Будем считать, что для нормализованных критериев решение многокритериальной задачи определяется в соответствии с принципом минимакса (гарантированного результата). Рассмотрим итерационную процедуру решения многокритериальной задачи, которая сводится к выполнению следующих действий.

1. Решение 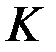задач однокритериальной оптимизации с целью нахождения управлений 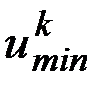и соответствующих им значений критериев 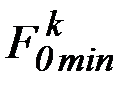и .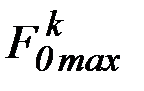

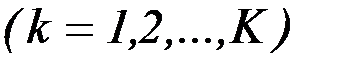2. Выбор начального приближения искомого управления 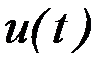из управлений 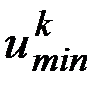и формирование множества значений .

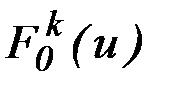3. Нормализация критериев при текущем приближении искомого управления.

4. Выбор наихудшего критерия 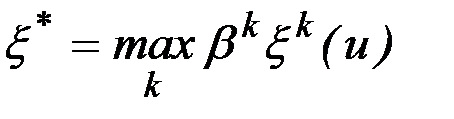, где 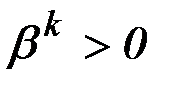- коэффициенты важности критериев, .

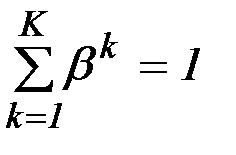5. Минимизация наихудшего критерия с целью нахождения следующего приближения текущего управления:

.

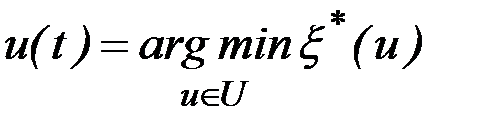Управление 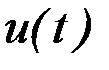принимается в качестве решения многокритериальной задачи, если на двух смежных итерациях значения наихудших критериев отличаются на значение, меньшее заданной точности, в противном случае выполняется следующая итерация, начиная с пункта 3.

Поиск приближенно-оптимального управления с учетом всех ограничений при выполнении пунктов 1 и 5 выполняется с помощью алгоритмов на основе метода последовательной линеаризации.

На каждой итерации решения многокритериальной задачи минимизируется наихудший критерий, в качестве которого может выступать любой критерий. В процессе поиска формируется приближение множества Парето, из которого в соответствии с коэффициентами важности критериев автоматически выбирается единственное решение.

Приведенная процедура может использоваться при формировании командного многокритериального управления. Для этого необходимо обеспечить выполнение требований к алгоритмам реального времени, в частности, априорную определенность числа выполняемых вычислительных операций.

В этом случае пункты 1 и 2 не выполняются, соответствующие им операции выполняются заранее: значения критериев 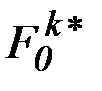, 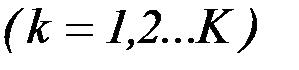не рассчитываются, а принимаются равными полученным при решении задачи формирования номинального управления, начальное приближение управления 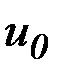принимается равным полученному при этом номинальному управлению. Количество итераций поиска задается заранее.

Приближенно-оптимальное управление можно получить с использованием аппроксимации в 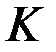-мерном пространстве критериев поверхности 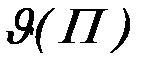, образованной сочетаниями критериев при 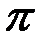-оптимальных управлениях. В соответствии со свойствами множества Парето поверхность 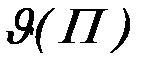строго монотонна и представляет собой левую нижнюю границу множества 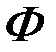. Поверхность 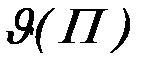является выпуклой, если множество 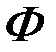выпукло. В этом случае поверхность 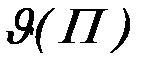может быть аппроксимирована гиперповерхностью.

В двухкритериальной задаче гиперболическая кривая (рис. ), проходящая через точки аппроксимаци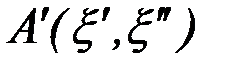и и 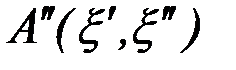, с центром в начале координат и асимптотами - координатными осями (в результате нормализации критериев) определяется уравнением

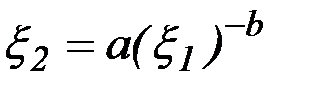
с коэффициентами

, .

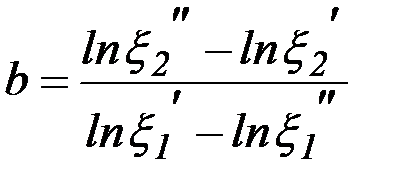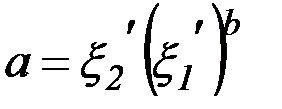В общем случае 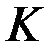критериев уравнение аппроксимирующей гиперповерхности, проходящей через 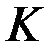точек аппроксимации 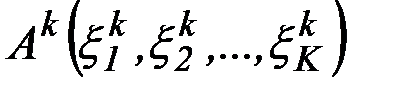( 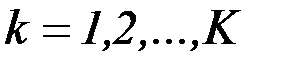) имеет вид

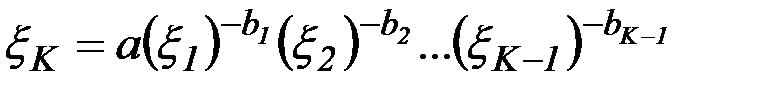
с коэффициентами 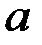, , 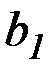,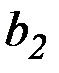…, , 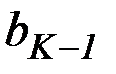получаемыми в результате решения системы уравнений

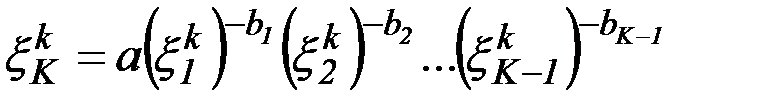
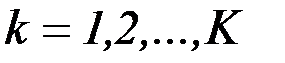. (6.47)

С учетом известного свойства нормализованные критерии при минимаксно-оптимальном управлении равны между собой. В двумерном случае точка, образованная сочетанием критериев при этом управлении, принадлежит биссектрисе первого квадранта. Вследствие этого координаты вершин аппроксимирующих гипербол (точки 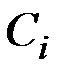, 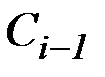на рис. 6.1) соответствуют приближенным решениям двухкритериальной задачи.

Для формирования управления, являющегося приближенным решением многокритериальной задачи, необходимо выполнить следующее.

1. Определить 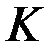векторов управления, обеспечивающих сочетания критериев, при которых значения ( 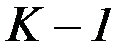) критериев фиксированы, а один критерий достигает минимума.

2. Определить коэффициенты аппроксимирующей поверхности путем решения системы (6.46).

3. Вычислить координаты вершины аппроксимирующей поверхности по формуле

.

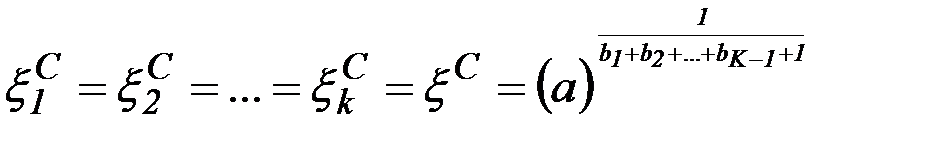Рис. 6.1. Формирование аппроксимирующих гипербол

Сочетание критериев в вершине аппроксимирующей поверхности и соответствующий вектор управления представляют собой приближенное решение многокритериальной задачи.

Уточнение приближенного решения может быть выполнено с помощью итерационной процедуры минимизации максимального для данного приближения критерия при фиксированных значениях других критериев. Управление, полученное в результате скалярной минимизации, позволяет сформировать соответствующую аппроксимирующую гиперповерхность, координаты вершины которой являются опорным управлением на следующей итерации.

Сходимость итерационной процедуры обеспечивается за счет выбора шага 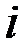-й итерации 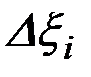(рис. 6.1) таким образом, чтобы выполнялось условие

,

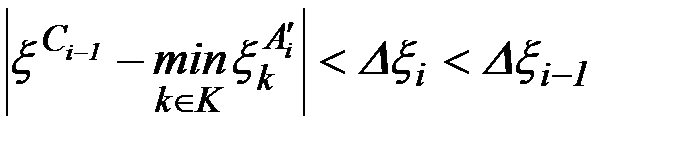за счет чего вершина аппроксимирующей гиперповерхности на каждой итерации оказывается между точками аппроксимаци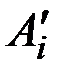и и .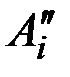

Шаг на 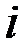-й итерации можно вычислить по формуле

.

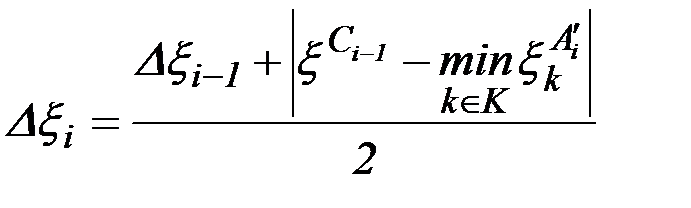Список литературы

1. Эльсгольц, Л.Э. Дифференциальные уравнения и вариационные исчисление / Л.Э. Эльсгольц. – М.: Наука, 1969. – 279 с.

2. Понтрягин, Л.С. Математическая теория оптимальных процессов / Л.С. Понтрягин, А.Г. Болтянский [и др.]; под ред. Л.С. Понтрягина. – М.: Наука, 1976. – 392 с.

3. Брайсон, А. Прикладная теория оптимального управления / А. Брайсон, Хо-Ю-ши. – М.: Наука, 1972. – 554 с.

4. Химмельблау, Д. Прикладное нелинейное программирование: пер. с англ. / Д. Химмельблау. – М.: Мир, 1975. – 534 с.

5. Кротов, В.Ф. Методы и задачи оптимального управления. / В.Ф. Кротов, В.И. Гурман. – М: Наука, 1973. – 279 с.

6. Беллман, Р. Динамическое программирование / Р. Беллман. – М.: ИЛ, 1960.

7. Малышев, В.В. Теория оптимальных систем: конспект лекций / В.В. Малышев. – М.: МАИ, 1973. – 196 с.

8. Основы автоматического управления/ под ред. В.С. Пугачева – М.: Наука, 1974. – 720 с.

9. Лебедев, А.А. Основы синтеза систем летательных аппаратов / А.А. Лебедев, В.Н. Баранов, В.Г. Бобронников [и др.]; под ред. А.А. Лебедева. – М.: Машиностроение, 1987. – 224 с.

10. Банди, Б. Методы оптимизации. Вводный курс / Б. Банди. – М.: Радио и связь, 1988. – 128 с.

11. Салмин, В.В. Оптимизация космических перелетов с малой тягой / В.В. Салмин. – М.: Машиностроение, 1987. – 208 с.

12. Интриллигатор, М. Математические методы оптимизации и экономическая теория / М. Интриллигатор. – М.: Прогресс. 1979. – 606 с.

13. Болтянский, В.Г. Математические методы оптимального управления. / В.Г. Болтянский . – М.: Наука, 1969. – 502 с.

14. Лебедев, В.Н. Расчет движения космического аппарата с малой тягой / В.Н. Лебедев // Математические методы в динамике космических аппаратов. Вып.5. – М.: ВЦ АН СССР, 1968. – 108 с.

15. Расчет и анализ движения летательных аппаратов. Инженерный справочник / под ред. С.А. Горбатенко. – М.: Машиностроение, 1971. – 438 с.

16. Дуров, В.Р. Боевое применение и боевая эффективность истребителей-перехватчиков / В.Р. Дуров. – М.: Воениздат, 1972. – 278 с.

17. Моисеев, Н.Н. Численные методы в теории оптимальных систем / Н.Н. Моисеев. – М.: Наука, 1971. – 424 с.

18. Сиразетдинов, Т.К. Методы решения многокритериальных задач синтеза технических систем / Т.К. Сиразетдинов. - М.: Машиностроение, 1988.

19. Федоренко Р.П. Приближенное решение задач оптимального управления / Р.П. Федоренко. – М.: Наука, 1978. – 488 с.

20. Федоренко Р.П. Введение в вычислительную физику. – М.: Изд-во Моск. физ.-тех. ин-та, 1994. – 528 с.

21. Шкадов Л.М. Механика оптимального пространственного движения летательных аппаратов в атмосфере / Л.М. Шкадов, Р.С. Буханова, В.Ф. Илларионов, В.П. Плохих. – М.: Машиностроение, 1972. – 240 с.

22. Салмин, В.В. Методы оптимального управления и численные методы в задачах синтеза технических систем / В.В. Салмин, Ю.Н. Лазарев, О.Л. Старинова. – Самара: Изд-во Самар. гос. аэрокосм. ун-та, 2007. – 160 с.

23. Лазарев, Ю.Н. Управление траекториями аэрокосмических аппаратов / Ю.Н. Лазарев. – Самара: Самар. науч. центр РАН, 2007. – 274 с.

24. Лазарев, Ю.Н. Управление траекториями аэрокосмических аппаратов. Теоретические основы, алгоритмы, результаты решения задач / Ю.Н. Лазарев. – Germany, Saarbrucken: LAP LAMBERT Academic Publishing, 2012. – 294 с.