Задача на условный экстремум

Исследуем на экстремум функционал, зависящий от 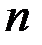функций,

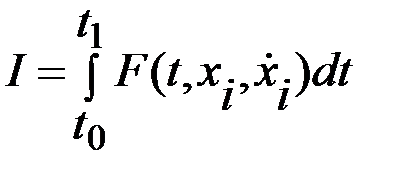
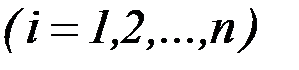
при граничных условиях

, ,

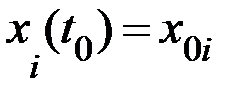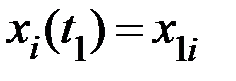и связях

.

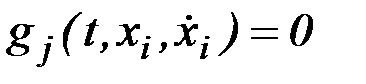
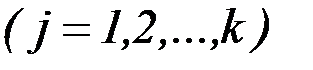Такая задача называется задачей на условный экстремум. Справедлива следующая теорема [1].

Теорема. Если функции 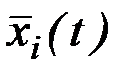обеспечивают условный экстремум функционалу 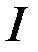, то существуют функции 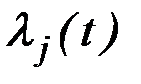, такие, что 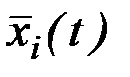являются экстремалями функционала

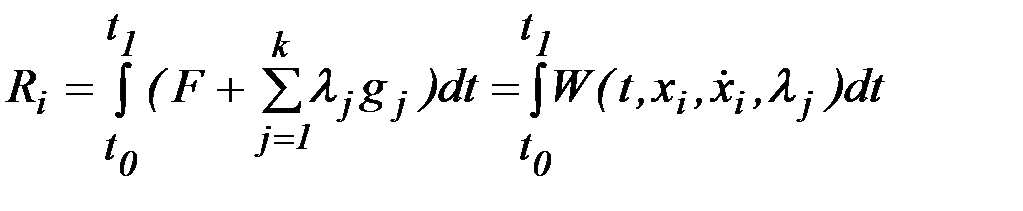, (2.16)

т.е. должны удовлетворять системе уравнений Эйлера

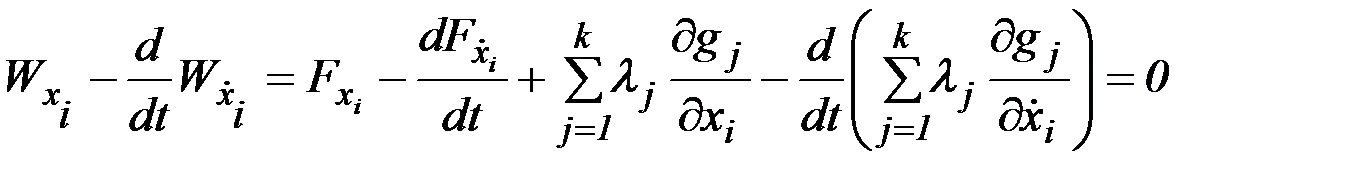, (2.17)

где , , ,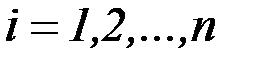

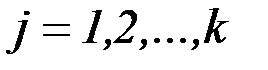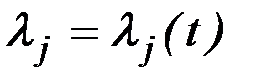и 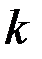условиям связи:

.

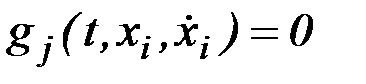Таким образом, при решении задачи составляются 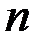дифференциальных уравнений второго порядка и 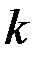уравнений первого порядка. Постоянные интегрирования определяются из граничных условий и условий связи.

2.9. Негладкие экстремали и условия

Вейерштрасса-Эрдмана

В некоторых классах вариационных задач решение достигается на негладких экстремалях (т.е. имеющих угловые точки). Предположим, что решается задача с закрепленными концами и что на искомой экстремали имеется точка излома 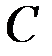, в которой терпит разрыв первая производная (рис. 2.6).

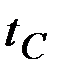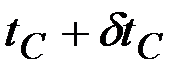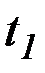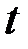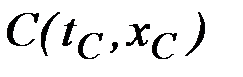Рис.2.6. Задача с закрепленными концами и изломом на экстремали

Найдем условия, которым должны удовлетворять решения с угловой точкой задачи об экстремуме функционала

.

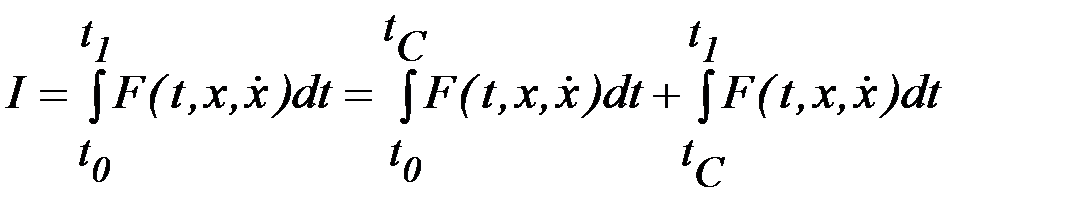Считая, что отдельные гладкие дуги ломаной экстремали являются интегральными кривыми уравнения Эйлера, что точка 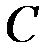может произвольно перемещаться, используя основную формулу для вариации функционала (2.11), получим

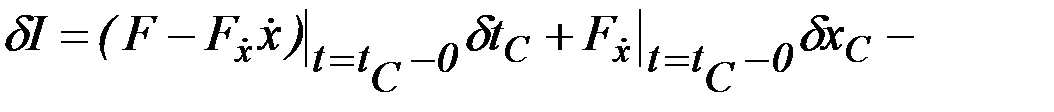
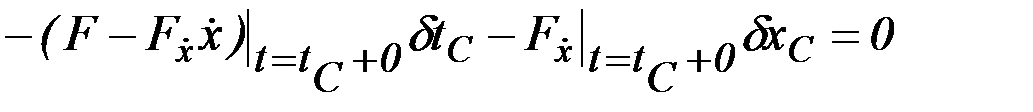, (2.18)

откуда

.

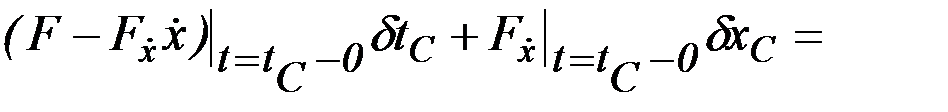
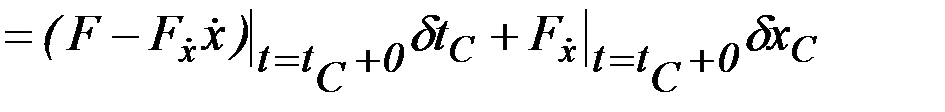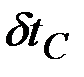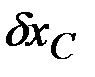Так как и независимы, имеем

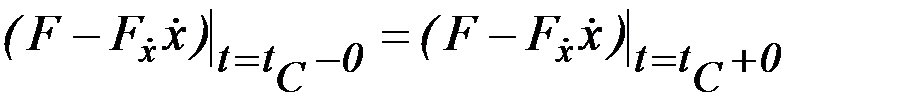, (2.19)

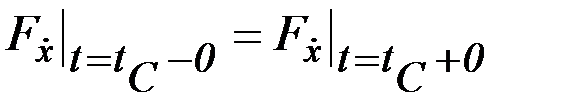. (2.20)

Эти условия называются условиями Вейерштрасса-Эрдмана и вместе с условиями непрерывности искомой экстремали позволяют определить координаты угловой точки .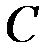

Каноническая форма уравнений Эйлера

Введем новые переменные и преобразуем основную формулу для вариации функционала (2.11):

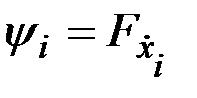, (2.21)

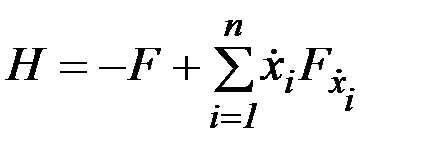, (2.22)

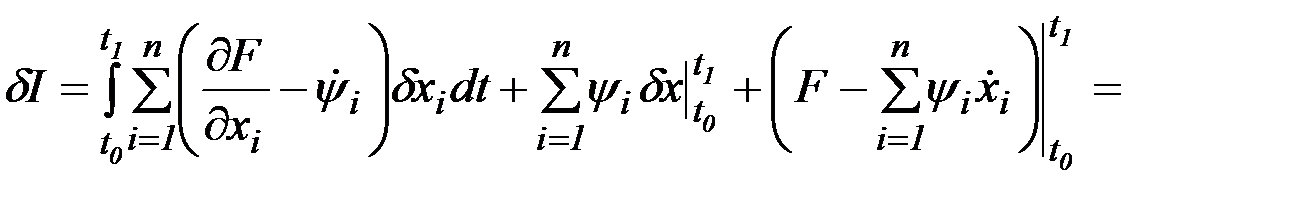
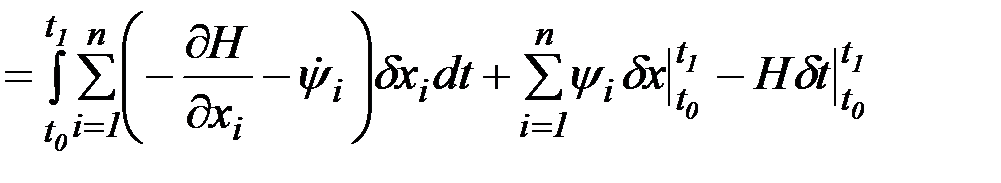. (2.23)

Система уравнений Эйлера

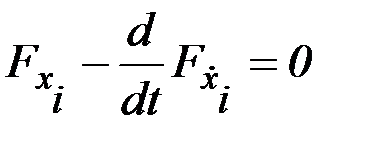
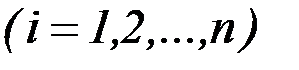(2.24)

заменяется системой 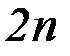уравнений первого порядка канонического вида:

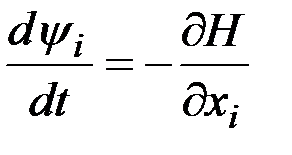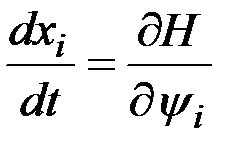
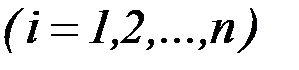, . (2.25)

Функция 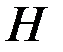называется функцией Гамильтона, а переменные 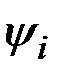- сопряженными переменными. Дифференциальные уравнения для сопряженных переменных (2.25) называются сопряженной системой уравнений.

Если функция 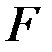не зависит явно от 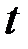, то функция 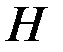является первым интегралом уравнений Эйлера. Действительно,

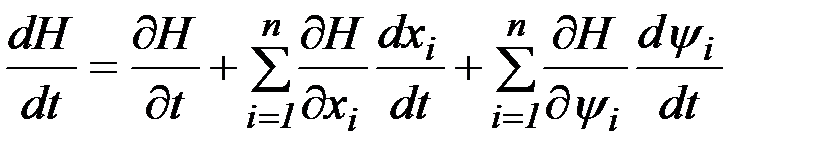, (2.26)

используя каноническую форму уравнений Эйлера, получим при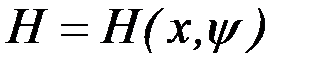

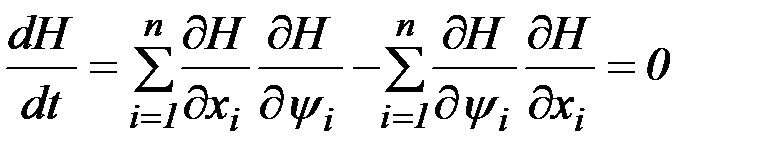, (2.27)

откуда следует, что .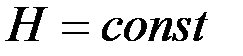

Рассмотрим некоторую функцию .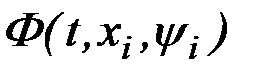

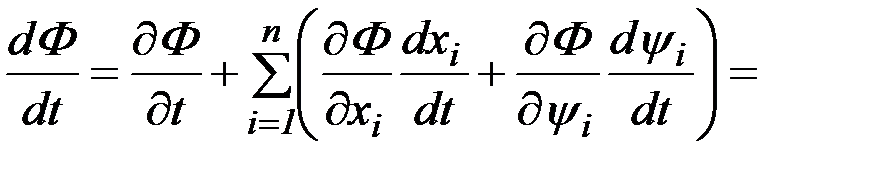
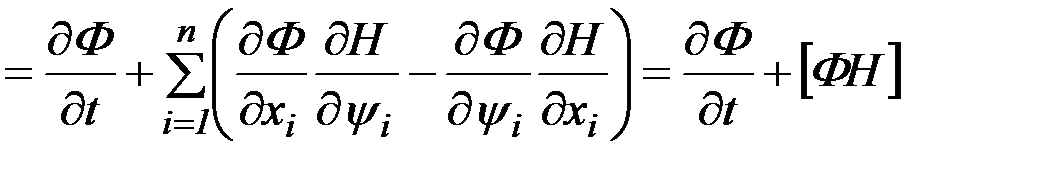. (2.28)

Выражение 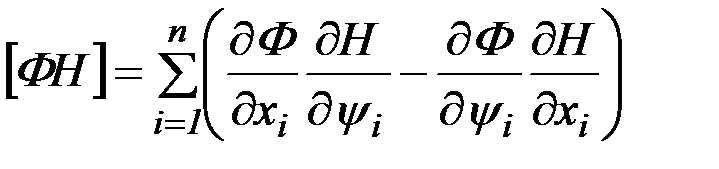называется скобкой Пуассона. Таким образом, чтобы функция 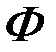, не зависящая явно от 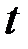, была первым интегралом уравнений Эйлера ( 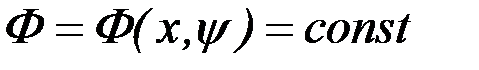), необходимо и достаточно, чтобы .

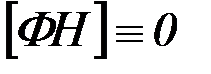Уравнение Гамильтона-Якоби

Рассмотрим центральное поле экстремалей с центром в точке 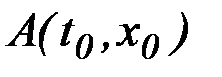для функционала

.

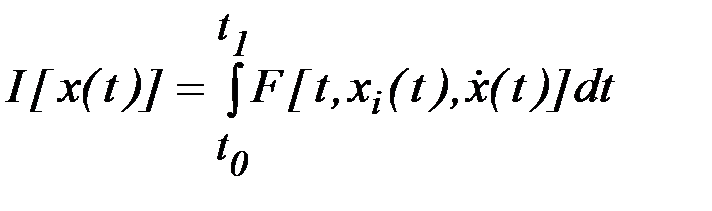
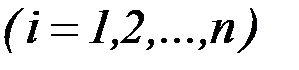На экстремалях поля функционал 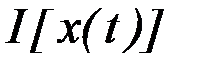превращается в функцию 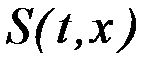координат второй граничной точки 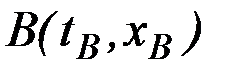. Воспользуемся выражением для вариации функционала (2.11)

.

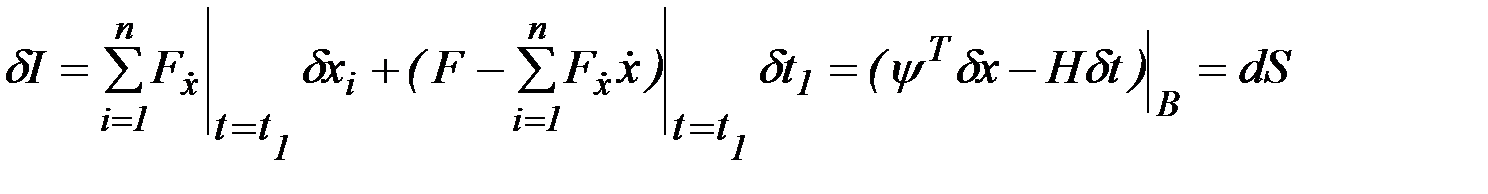(2.29)

С другой стороны .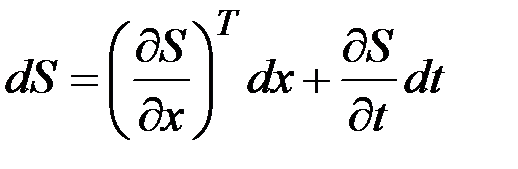

Для точки 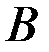: 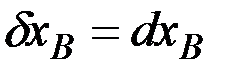, , 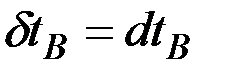тогда

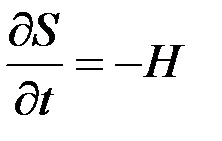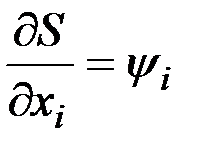, . (2.30)

Следовательно,

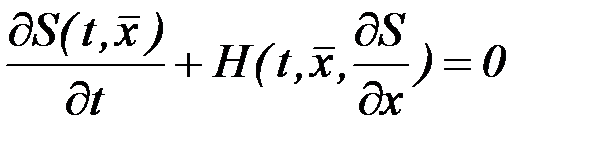. (2.31)

Это уравнение называется уравнением Гамильтона-Якоби.

В этом случае решение канонической системы равносильно решению дифференциального уравнения в частных производных относительно неизвестной функции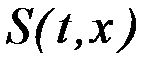

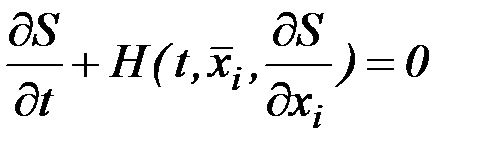
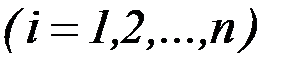(2.32)

с граничным условием .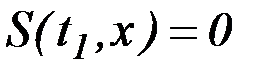

2.12. Вторая вариация функционала.

Необходимое условие слабого минимума функционала

Для нахождения необходимого условия слабого минимума функционала введем понятие второй вариации функционала. Функционал 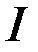имеет вторую вариацию, если его приращение можно представить в виде

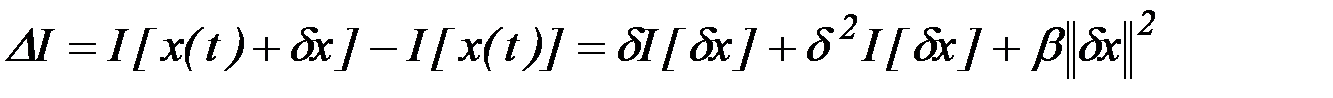, (2.33)

где 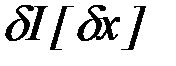- линейный относительно вариации функции 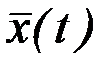функционал (первая вариация функционала),

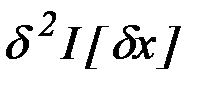- квадратичный относительно 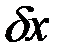функционал (вторая вариация функционала),

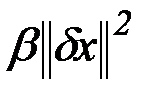- содержит члены высших порядков малост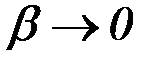и ( при ).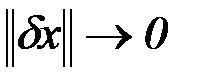

Теорема. Для того, чтобы функционал достигал своего минимума на кривой 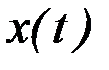, необходимо чтобы выполнялись условия

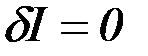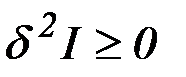, . (2.34)

Доказательство

Пусть имеется кривая 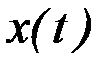, которая неограниченно приближается к экстремали 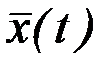. Это означает, что 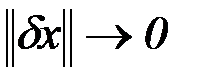, т.е. кривые сближаются. Тогда 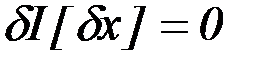, , 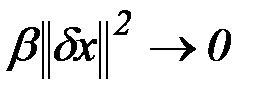следовательно, знак 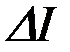определяется знаком 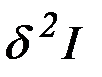. Это означает, что неотрицательность второй вариации обеспечивает минимум функционала.

Получим формулу для второй вариации функционала в задаче с закрепленными концами. Зададим функционал

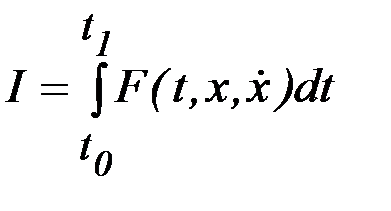
с граничными условиями 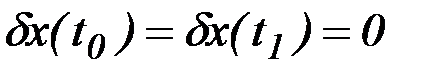. В этом случае первая и вторая вариации функционала определяются формулами

,

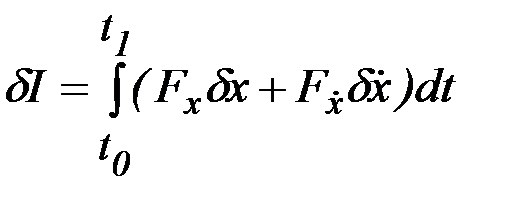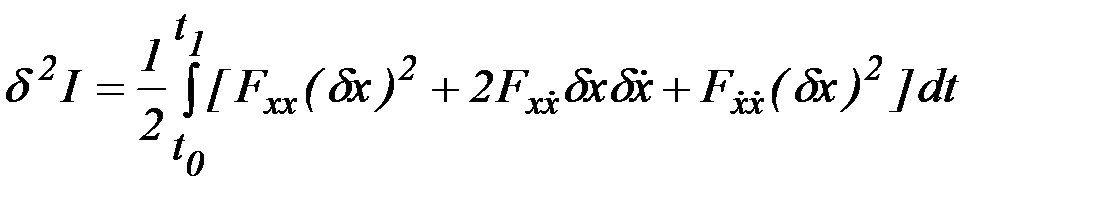. (2.35)

Интегрируя по частям среднее слагаемое в подынтегральном выражении формулы (2.35), получим

.

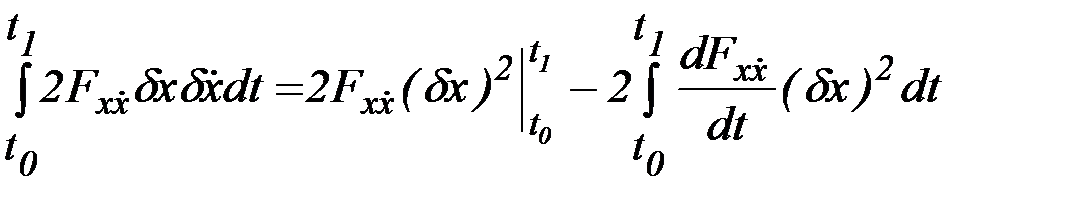Тогда с учетом граничных условий получим

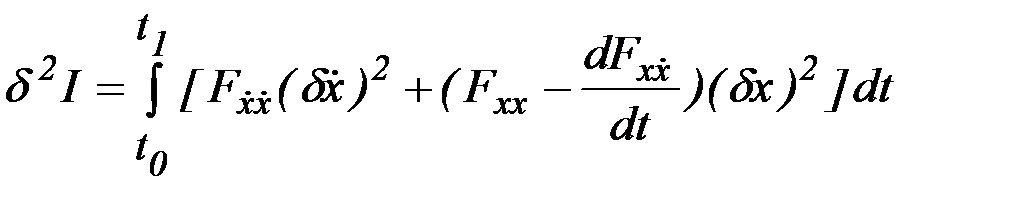. (2.36)

Получим условие, при котором 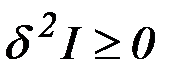. Если 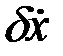мала, то с учетом граничных условий мала и сама 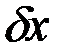, а если мала 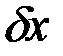, то 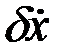может быть не мала. Поэтому слагаемое 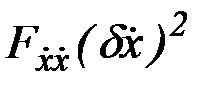в выражении для 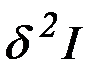играет определяющую роль и знак второй вариации функционала определяется знаком 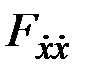. Следовательно, необходимым условием минимума функционала 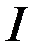является условие

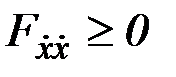. (2.37)

Это условие называется условием Лежандра.

Замечание. Для случая функционалов, зависящих от 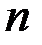функций 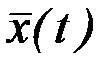условие Лежандра сводится к требованию положительной определенности матрицы

.

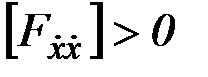Условие Лежандра, как и условие Эйлера, носит локальный характер, т.е. относится не к кривой в целом, а к ее отдельным точкам и поэтому не является достаточным для экстремума.