Задача с подвижными границами
При исследовании функционала (2.1) на экстремум предположим, что одна или обе граничные точки могут перемещаться по заданным кривым 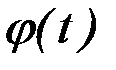 и
и 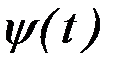 . Эта задача называется задачей с подвижными границами. В этом случае класс допустимых кривых расширяется. Поэтому если на кривой
. Эта задача называется задачей с подвижными границами. В этом случае класс допустимых кривых расширяется. Поэтому если на кривой 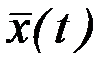 достигается экстремум в задаче с подвижными границами, то экстремум тем более достигается по отношению к более узкому классу кривых, имеющих общие граничные точки с кривой
достигается экстремум в задаче с подвижными границами, то экстремум тем более достигается по отношению к более узкому классу кривых, имеющих общие граничные точки с кривой 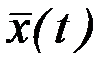 . Следовательно, функция
. Следовательно, функция 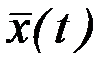 должна быть решением уравнения Эйлера, и все кривые
должна быть решением уравнения Эйлера, и все кривые 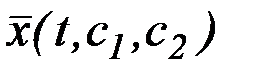 , на которых реализуется экстремум в задаче с подвижными концами, должны быть экстремалями.
, на которых реализуется экстремум в задаче с подвижными концами, должны быть экстремалями.
Общее решение уравнения Эйлера содержит две произвольные постоянные, для определения которых необходимо иметь два условия. В задаче с закрепленными концами такими условиями были 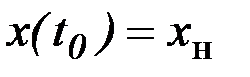 и
и 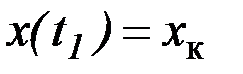 . В задаче с подвижными границами одно или оба эти условия отсутствуют. Недостающие условия для определения произвольных постоянных должны быть получены из основного необходимого условия экстремума - равенства нулю вариации
. В задаче с подвижными границами одно или оба эти условия отсутствуют. Недостающие условия для определения произвольных постоянных должны быть получены из основного необходимого условия экстремума - равенства нулю вариации 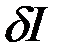 .
.
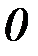 |
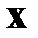 |
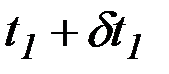 |
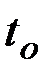 |
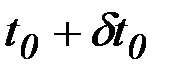 |
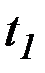 |
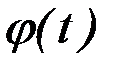 |
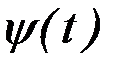 |
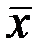 |
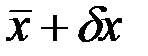 |
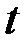 |
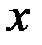 |
| Рис.2.5. Задача с подвижными концами |
Рассмотрим следующую задачу с подвижными границами. Найти экстремум функционала
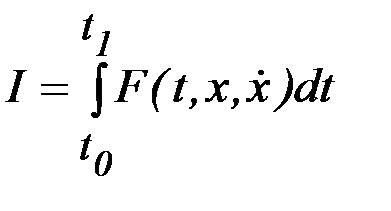 ,
,
определенного на кривых, концы которых могут перемещаться по линиям 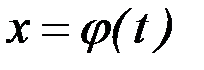 и
и 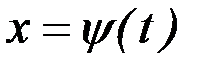 (рис. 2.5).
(рис. 2.5).
Искомые кривые (экстремали) должны удовлетворять уравнению Эйлера, поэтому в выражении для вариации функционала остается только внеинтегральный член. Учитывая, что
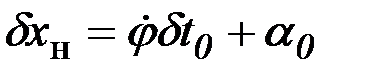 ,
,
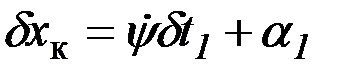 ,
,
где 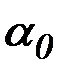 и
и 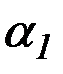 - бесконечно малые величины, имеем
- бесконечно малые величины, имеем
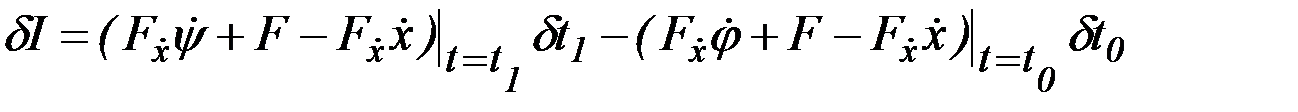 .
.
Вариации независимой переменной 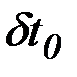 и
и 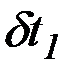 не равны нулю, поэтому выражения
не равны нулю, поэтому выражения 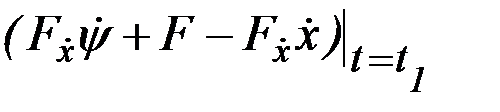 ,
, 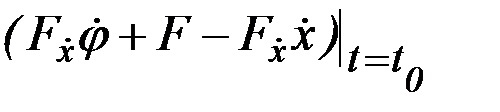 должны обращаться в нуль:
должны обращаться в нуль:
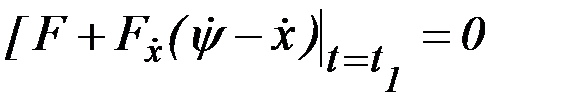 , (2.13)
, (2.13)
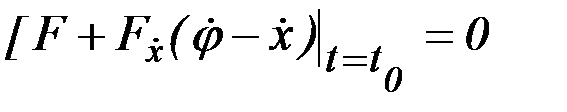 . (2.14)
. (2.14)
Эти граничные условия называются условиями трансверсальности. Про искомую экстремаль 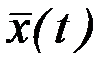 говорят, что она трансверсальна кривым
говорят, что она трансверсальна кривым 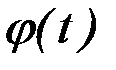 и
и 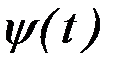 . Условия трансверсальности позволяют определить две постоянные интегрирования после решения уравнения Эйлера.
. Условия трансверсальности позволяют определить две постоянные интегрирования после решения уравнения Эйлера.
Изопериметрическая задача
Изопериметрическими задачами в узком смысле этого слова называются задачи об отыскании геометрической фигуры максимальной площади при заданном периметре.
В настоящее время изопериметрическими задачами называется значительно более широкий класс задач, а именно, все вариационные задачи, в которых требуется определить экстремум функционала
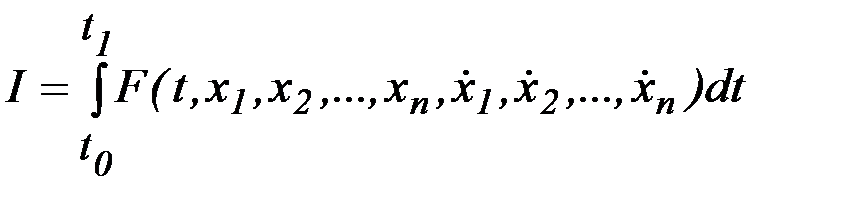 ,
,
при наличии так называемых изопериметрических условий
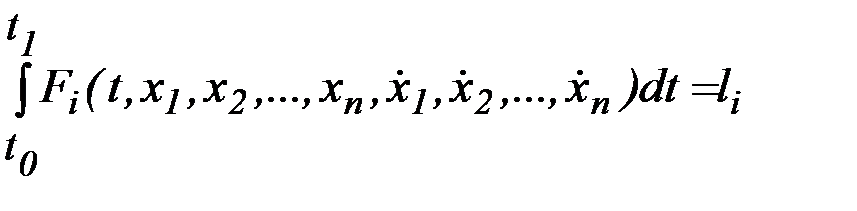
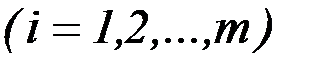 ,
,
где 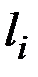 - постоянные, а
- постоянные, а 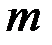 может быть больше, меньше или равно
может быть больше, меньше или равно 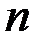 .
.
Рассмотрим следующую изопериметрическую задачу.
Среди всех кривых 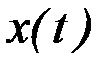 , удовлетворяющих условиям
, удовлетворяющих условиям 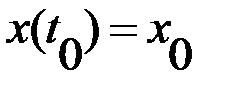 ,
, 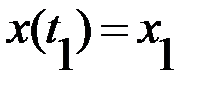 , на которых функционал
, на которых функционал
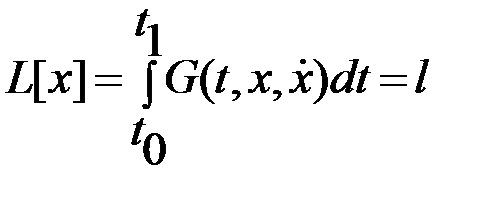 ,
,
найти такую, которая дает экстремум функционалу
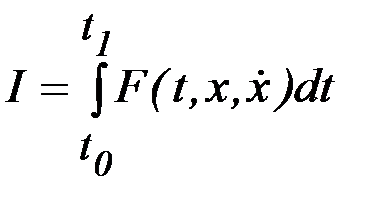 .
.
Пусть 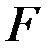 и
и 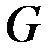 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 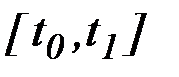 . Предположим, что искомая кривая не является экстремалью
. Предположим, что искомая кривая не является экстремалью 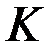 , тогда имеет место теорема [1].
, тогда имеет место теорема [1].
Теорема. Если кривая 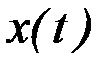 обеспечивает экстремум функционала
обеспечивает экстремум функционала 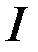 и удовлетворяет условиям
и удовлетворяет условиям 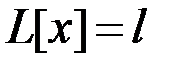 ,
, 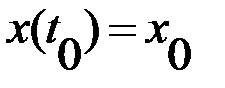 ,
, 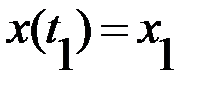 , но не является экстремалью
, но не является экстремалью 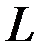 , то существует такое число
, то существует такое число 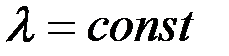 , что
, что 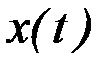 является экстремалью функционала
является экстремалью функционала
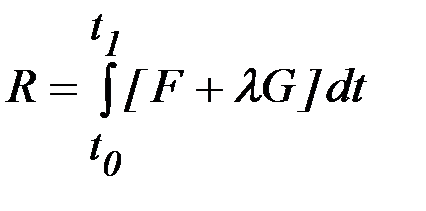 . (2.15)
. (2.15)
Этот результат используется следующим образом. Составляется уравнение Эйлера для функционала 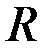 . Получается дифференциальное уравнение второго порядка и находится его общее решение, которое содержит параметр
. Получается дифференциальное уравнение второго порядка и находится его общее решение, которое содержит параметр 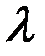 и две произвольные постоянные. Эти три величины определяются из граничных условий и условия
и две произвольные постоянные. Эти три величины определяются из граничных условий и условия 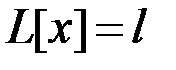 .
.
