О среднем значении при известной и неизвестной дисперсиях.

Гипотеза – это предположение о том, что эмпирическое распределение описывается некоторым теоретическим распределением, или о при­надлежности выборочных данных к одной генеральной совокупности, или относительно одного или нескольких параметров совокупности и т. д., подвергаемое статистической проверке.

Статистической гипотезой, обозначаемой Н,называется любое предположение относительно вида или параметров распределения слу­чайной величины X, которое может быть проверено по результатам выборки.

Статистическим критерием для проверки гипотез Н₀, H₁, ..., H_m называют случайную величину δ=δ(Х), принимающую значения 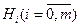, т.е. .

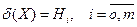Критической областью для данного статистического критерия δ гипотезы H₀ называется множество значений статистической характе­ристики гипотезы, которые, согласно правилу δ, приводят к отвержению гипотезы Н₀.

Проверка гипотез проводится по следующей схеме.

1. Формулировка основной и альтернативной гипотез.

2. Выбор соответствующего уровня значимости критерия: 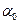= 0,05; 0,01; 0,001.

3. Определение объема выборки n (если выборки нет).

4. Определение статистической характеристики критерия.

5. Вычисление критической области и области принятия гипотезы.

6. Формулировка правила проверки гипотезы: гипотеза Н₀ прини­мается при заданном уровне значимости α, если выборочное значение статистической характеристики попадает в область принятия гипотезы; гипотеза Н₀ отвергается, если выборочное значение статистической характеристики попадает в критическую область.

Если критические области располагаются слева и справа от мате­матического ожидания случайной величины δ, то критическая область называется двусторонней, а критерий δ – двусторонним критерием значимости. Если же критическая область располагается слева или справа от математического ожидания случайной величины δ, то крити­ческая область называется односторонней, а критерий — односторон­ним.

Рассмотрим нормально распределенную случайную величину X с неизвестным математическим ожиданием, среднее квадратическое от­клонение которой σ известно. Чтобы проверить гипотезу H₀: 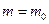т. е. проверить предположение о равенстве математического ожидания всей совокупности значению 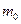при альтернативной гипотезе H₁ : 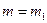нужно воспользоваться статистической характеристикой

.

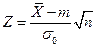Если 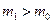, то критическая область [ 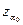;+∞) определяется из равенства P(Z ) = .

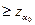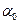По таблице значений функции

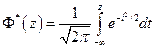
находим значение 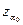, такое, что Ф*( 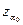) = 1– .

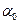Тогда, если Z_pacч 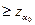то, гипотеза H₀ отвергается; в противном случае нет оснований отвергать нулевую гипотезу.

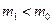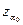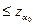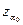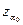Если , то критическая область (–∞, ] определяется из равенства P(Z )=Ф*( )= . Если Z_paсч 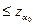, то гипотеза H₀ отвергается; в про­тивном случае нет оснований отвергать нулевую гипотезу.

Если же альтернативная гипотеза Н₁ определена не однозначно, то критическая область определяется так, чтобы ей принадлежали все значения статистической характеристики Z, которые не больше – 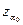и не меньш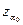е , где 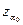определяется из равенства

P(Z<– 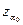)=P(Z> )=

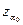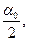
т. е. Ф*( 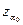) = 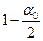. При выполнении неравенства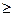 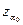Z или Z 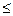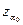гипотеза H₀ отвергается; в противном случае нет оснований отвергать нулевую гипотезу.

В случае, когда наблюдаемая случайная величина X подчиняется нормальному закону распределения с неизвестным средним квадратич­еским отклонением, статистической характеристикой служит величина

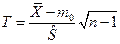, (3.1)

имеющая закон распределения Стьюдента с 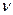=n–1 степенями, сво­боды.

Для того чтобы при заданном уровне значимости 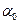проверить нулевую гипотезу Н₀ : 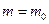, при альтернативной гипотезе Н₁ : 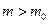, по таблице распределения Стьюдента находят квантиль 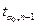из равенства .

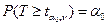Если T_расч 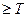,то нулевая гипотеза H₀ отвергается на уровне значимости α; в противном случае (если T_расч< t_α;n–1) нет оснований отвергать нулевую гипотезу H₀.

При альтернативной гипотезе H₁: 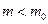, по таблице распределения Стьюдента находят квантиль 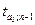из равенства .

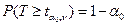Если T_расч. 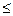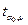то нулевая гипотеза Н₀ отвергается на уровне значимости 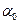, в противном случае (T_расч> 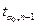) нет оснований от­вергать нулевую гипотезу.

При альтернативной гипотезе H₁: m 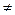m₀, сравнивают модуль стати­стической характеристики Т с квантилем 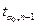распределения Стьюдента, найденным из равенства .

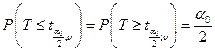Если |Т_расч|< 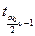то нет оснований отвергать нулевую гипо­тезу Н₀; в противном случае (|Т_расч|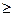 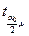) нулевая гипотеза Н₀ отвергается.

Задачи

3.1. Предельная сила натяжения прядильной нити в среднем равна 20 г. Выборку нити из 64 мотков обработали некоторым химическим составом. После просушки была заново измерена предельная сила на­тяжения нити. В среднем она оказалась равной 21 г. Предполагая, что среднее квадратичное отклонение 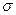предельной силы натяжения нити равно 2 г до и после обработки химическим составом, проверить гипотезу о том, что эта обработка не увеличила предельной силы натя­жения нити.

Решение. Обозначим среднюю предельную силу натяжения пря­дильной нити через М(Х) = .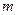

Решение задачи разобьем на ряд этапов.

1. Формулировка нулевой и альтернативной гипотез. Сформулируем следующие гипотезы: основная гипотеза Н₀ : 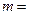20, альтернативная гипотеза H₁ : 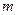>20 (односторонняя проверка, так как нас интересует, увеличится ли предельная сила натяжения нити в среднем после обра­ботки химическим составом).

2. Выбор соответствующего уровня значимости α₀. Возьмем α₀=0,05.

3. Определение объема выборки. В условии выборка определена (n=64).

4. Выбор статистики критерия. В качестве статистики возьмем
величину

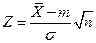, (3.2)

имеющую приближенное стандартное нормальное распределение при условии, что гипотеза Н₀ верна.

5. Вычисление критической области и области принятия гипотезы. При 5%-м уровне значимости для односторонней проверки наибольшее значение величины Z, при котором Н₀ еще не отвергается, будет равно 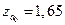. Это наибольшее значение определяется из таблицы 3.1. Таким образом, область принятия гипотезы – полуинтервал (–∞;1,65), а крити­ческая область – интервал [1,65;+∞).

Таблица 3.1

Критическое значение статистики (3.2)	Уровень значимости,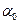
0,05	0,01	0,001
Односторонняя проверка	1,65	2,33	3,08
Двусторонняя проверка	1,69	2,58	3,27

6. Формулировка правила проверки гипотезы.

Предельная сила натяжения прядильной нити в среднем увеличится, если значение статистики Z, вычисленное по выборке, больше 1,65. В других случаях считаем, что предельная сила натяжения нити в сред­нем не увеличится.

7. Проверка гипотезы. По выборочным данным находим, что

.

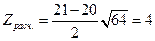Предельная сила натяжения прядильной нити в среднем увеличится, так как Z_расч=4>1,6= 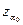. Этот вывод будет неверным менее чем для 5% всех случаев.

Ответ: предельная сила натяжения нити в среднем увеличивается.

3.2. Для анализа выпуска химической смеси производится случайная выборка из дневной партии и определяется процентное содержание воды двумя способами. Результаты, полученные в течение 8 дней, указаны в таблице 3.2.

Таблица 3.2

Способ определения процентного содержания воды	Дни
А
В

Необходимо проверить гипотезу о том, что методы анализа суще­ственно различаются между собой.

Решение. Как видно из таблицы 3.2, имеется заметное различие в процентном содержании воды в химической смеси. Эти колебания не дают возможности определить различие в способах определения про­центного содержания воды.

Наблюдения, в которых результаты экспериментов объединены в пары и каждая пара представляет собой самостоятельную эксперимен­тальную единицу, исследуем, применив критерий сравнения. Каждая пара дает одно сравнение, которое определяет меру эффекта некоторого действия.

Обозначим через d разность результатов каждой пары. Оно будет иметь нормальное распределение со средним 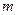и средним квадратичным отклонением S. Значения величины d для дней 1, 2, …, 8 будут равны соответственно: – 3;1; –2; 0; – 1;1; –5; –2.

Сформулируем следующие гипотезы: основная гипотеза Н₀ : 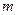= 0 (способ определения процентного содержания воды не имеет значения); альтернативная гипотеза Н₁: 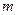>0 (способ В превосходит способ А для определения процентного содержания воды).

Гипотеза Н₁ односторонняя, поэтому определяем одностороннюю критическую область при α₀=0,05 и n=8.

Статистикой является величина (3.1)

,

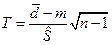имеющая t-распределение Стьюдента с 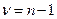степенями свободы.

Так как критическое значение 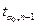для 7 степеней свободы равно 1,89, областью принятия гипотезы является интервал (–∞; 1,89).

Если значение T, вычисленное по данным выборки, не меньше 1,89, то можно сделать вывод о том, что способ В имеет преимущество перед способом А. Если Т_расч 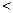1,89, то гипотеза Н₀ принимается, т. е. способы А и В равнозначны.

По данным выборки имеем:

.

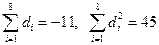Отсюда

.

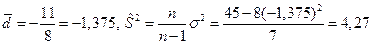Поэтому

.

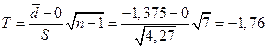Так как –1,76<1,89, то можно утверждать, что при 5%-м уровне значимости методы анализа процентного содержания воды равносильны. Таким образом, различия между способами А и В не установлено.

Ответ: методы анализа не различаются.

3.3. По паспортным данным автомобильного двигателя расход топлива на 100 км пробега составляет 8 л. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки проводятся испытания 50 случайно отобранных автомобилей с модернизированным двигателем. Среднее арифметическое расхода топлива на 100 км пробега, у отобранных автомобилей, по результатам испытаний составило 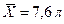. Предположим, что случайная величина Х характеризующая расход топлива на 100 км пробега подчиняется нормальному закону распределения со средним m и дисперсией 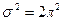. Проверить гипотезу о том, что модернизация двигателя не повлияла на расход топлива.

Решение. В данной задаче нужно проверить гипотезу о математическом ожидании m нормального распределения генеральной совокупности. Проверку гипотезы проведем по этапам:

1. Проверяемая основная гипотеза H₀ состоит в том, что математическое ожидание m нормального распределения случайной величины X составляет 8 л, т.е. H₀ : m=8л, при альтернативной гипотезе H₁: 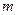<8л (односторонняя проверка; нас интересует, будет ли среднее меньше гарантированного минимума).

1. Выбираем уровень значимости .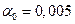

2. Объем выборки задан, n=50.

3. В качестве статистической характеристики выбираем случайную величину:

,

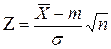имеющую нормальное распределение с параметрами m=0, 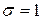: N(0;1).

5. Так как альтернативная гипотеза H₁: m<8, то критическая область определяется неравенством Z_расч.< 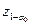. По таблице 1 (в приложении 1) находим из равенства 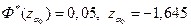. Таким образом, область принятия гипотезы – интервал ( 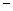∞; - 1,645).Критическая область 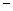полуинтервал .

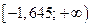6. Правило проверки гипотезы.

По выборочным данным находим значение статистической характеристики:

.

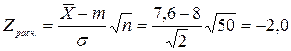Поскольку Z_расч.=-2,0< 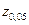=-1,645, то гипотеза H₀ отвергается и принимается альтернативная гипотеза H₁: следует считать, что изменения конструкции двигателя привело к уменьшению расхода топлива.

Ответ: Изменение конструкции двигателя привлекло к уменьшению расхода топлива.

3.4.Известно, что при некотором технологическом процессе за смену (n=8 часов) выпускается в среднем 350 единиц изделия. После некоторых изменений в производственном процессе за смену стало выпускаться в среднем 355 изделий. Предположим, что случайная величина X характеризующая число выпускаемых изделий за смену (n=8 часов) подчиняется нормальному закону распределения со средним m и дисперсией 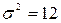единиц. Проверить гипотезу о том, что модернизация производственного процесса не повлияла на увеличение производства изделий при уровне значимости α₀=0,05.

3.5. В соответствии с техническими условиями среднее время безотказной работы приборов из партии, содержащей 10000 приборов равно 1000 часам. При контрольной проверке 36 приборов из данной партии среднее время безотказной работы составило 950 часов. Предположим, что случайная величина X характеризующая время безотказной работы прибора подчиняется нормальному закону распределения со средним m и дисперсией 100 часов. Проверить гипотезу о том, что вся партия приборов не удовлетворяет техническим условиям при уровне значимости α₀=0,05.

3.6. Технология производства некоторого вещества дает в среднем 640 кг вещества в сутки (n=8 часов). После некоторых изменений в производственном процессе стали получать в среднем в сутки 700 кг вещества. Предполагается, что случайная величина X, характеризующая производство вещества, подчиняется нормальному закону распределения со средним m и дисперсией 100 кг. Проверить гипотезу о том, что изменения в технологическом процессе привели к повышению производительности.

3.7. Из статистического сборника известно, что 7% всех застраховавших свою жизнь умирает по достижении 60 лет. В группе из 1000 человек этого возраста, работающих в сфере обслуживания, умерло 85 человек. Проверить гипотезу о том, что застрахованные люди, работающие в сфере обслуживания, чаще умирают в 60 лет, чем все остальные застрахованные. Принять α₀=0,05.

Решение. В данной задаче нужно сравнить вероятность появления события в каждом испытании с заданной вероятностью p₀=0,07.

1. Сформулируем основную гипотезу H₀, состоящую в том, что вероятность застрахованного человека умереть по достижении 60 лет равна 0,07, т.е. H₀ : p=0,07; при альтернативной гипотезе H₁, состоящей в том, что застрахованные люди, работающие в сфере обслуживания чаще умирают в 60 лет, чем все остальные, т.е. H₁ : p>0,07.

2. Выбираем уровень значимости: α₀=0,05.

3. Объем выборки задан: n=1000.

4. В качестве статистической характеристики выбираем случайную величину:

,

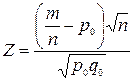имеющую распределение, близкое к нормальному распределению N(0,1).

5. Так как альтернативная гипотеза H₁ : p>0,7, то критическая область при уровне значимости α₀ определяется неравенством 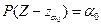, квантиль 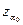находим по таблице 1 (приложение 1) из равенства 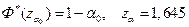. Следовательно, область принятия гипотезы – интервал (-∞;1,645), а критическая область – полуинтервал [1,645;+∞).

6. По выборочным данным находим значение статистической характеристики

.

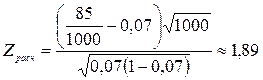Поскольку Z_расч=1,89>z_0,95=1,645 лежит в критической области, то с вероятностью 0,95 принимается альтернативная гипотеза H₁. Следовательно, застрахованные люди, работающие в среде обслуживания, чаще умирают в 60 лет, чем все остальные застрахованные.

Ответ: Застрахованные люди, работающие в среде обслуживания, чаще умирают в 60 лет, чем все остальные застрахованные.

3.8. Количество бракованных деталей в партии не должно превышать 3%. В результате контроля 100 деталей из этой партии обнаружено 5 бракованных. Можно ли считать, что процент брака превосходит допустимый при α₀=0,05?

3.9. При исследовании 100 корпусов упаковки стеклянных изделий, случайным образом выбранных из большой партии этих изделий, оказались, что 8-ем из них не имеют необходимой прочности. Согласуются ли эти данные с утверждением о том, что данная партия содержит более чем 90% прочных корпусов, если α₀=0,05.

3.10. Из суточной продукции кондитерского цеха случайным образом отобрано и проверено 20 кондитерских продукта. При этом 5 единиц продукта признаны не соответствующими госту. Можно ли считать, что годная продукция кондитерского цеха составляет 99%, если α₀=0,05?

3.11.Для исследования на прочность волокон некото­рого вида после химической обработки было отобрано и пронумеровано шесть мотков волокон. Каждый отобран­ный моток был разделен пополам, одна половина под­верглась химической обработке, другая – нет. Затем с помощью прибора, измеряющего прочность волокон, была замерена прочность (в %) двенадцати кусков во­локон. Результаты представлены в таблице 3.3.

Таблица 3.3

Номер исследуемого куска
Обработанная половина	18,1	17,3	19,1	18,4	17,2	16,7
Необработанная половина	16,3	17,0	18,4	17,6	17,0	16,2

Увеличила ли химическая обработка прочность во­локна?

3.12. Обследование выпущенных видеомагнитофонов показало, что 5% из них имеют брак. Проверить гипотезу Н₀ : вероятность того, что магнитофон бракованный, равна 0,05, взяв в качестве уровня значимости критерия α₀= 0,01. Объем производимой выборки n принять равным 400 видеомагнитофонов. Какое нужно принять решение относительно гипотезы Н₀, если в произведенной выборке окажется 26 бракованных видеомагнитофонов?

3.13. Считается, что завод, производящий за неделю 1000 телевизоров, работает удовлетворительно, если в среднем частость бракованных телевизоров при контроле качества не превышает 3%. Допустим, что в течение некоторой недели было забраковано 38 телевизоров. Необходимо ли директору завода провести более полную проверку качества изготовления телевизоров на производственной линии или же следует отнести высокий процент дефектной продукции этой недели за счет случайных изменений в условиях производства? Воспользоваться односторонней проверкой гипотезы с 5%-м уровнем значимости.

3.14. По утверждению фирмы, средний размер дебиторского счета 187,5 тыс. р. Ревизор составляет случайную выборку из 50 счетов и обнаруживает, что средняя арифме­тическая выборки равна 175 тыс. р. при среднем квадра­тичном отклонении 35 тыс. р. Может ли оказаться в действительности правильным объявленный размер дебитор­ского счета? Уровень значимости принять равным 0,05 и 0.01.

3.15. По техническим условиям средняя прочность на разрыв троса составляет 2000 кг. В результате испытаний 20 кусков троса было установлено, что средняя прочность на разрыв равна 1955 кг при средней ошибке 25 кг. Удо­влетворяет ли образец троса техническим условиям? Уровень значимости принять равным 0,05.

3.16. Фирма, производящая электрические лампочки, утверждает, что среднее время безотказной работы лампочек мощностью 120 Вт равно по меньшей мере 800 ч со средним квадратичным отклонением 120 ч. Из некоторой партии 120-ваттных лампочек производится выборка 25 лампочек, для которой выборочное среднее времени работы лампочек оказалось равным 750 ч. Можно ли на основании этого сказать, что исследуемая выборка лампочек не удовлетворяет гарантии?

3.17.Поставщик трехпроходных ламп накаливания утверждает, что их средний срок службы равен 2500 ч. Для выборки из 37 ламп средний срок службы равен 2325 ч при среднем квадратичном отклонении 600 ч. Можно ли считать, что при уровне значимости α₀=0,05 срок службы ламп оказался значительно ниже гарантированного поставщиком?

3.18. Предельная сила натяжения прядильной шерстя­ной нити в среднем равна 8 г. Выборку нити из 64 мотков обработали некоторым химическим составом. После просушки была заново измерена предельная сила натяжения нити. В среднем она оказалась равной 8,5 г. Предполагая, что среднее квадратичное отклонение предельной силы натяжения нити равно 2 г до и после обработки химическим составом, проверить гипотезу о том, что эта обработка не увеличила предельной силы натяжения нити. Сделать проверку при уровне значимости 0,05 и 0,01.