Принцип максимального значения

В этом параграфе мы докажем свойство решений одномерного уравнения теплопроводности, которое называется принципом максимального значения. Оно может быть сформулировано как теорема.

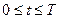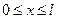Т е о р е м а. Если функция u(x,t), определенная и непрерывная в замкнутой области и , удовлетворяет в этой области уравнению теплопроводности

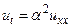, (40)

то максимальное и минимальное значения функции u(x,t) достигаются или в начальный момент времени или в граничных точках x = 0 или x = l.

Функция 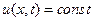, очевидно, удовлетворяет уравнению (40) и достигает своего максимального (минимального) значения в любой точке. Однако это не противоречит теореме, так как из её условия следует, что если максимальное (минимальное) значение достигается внутри области, то оно также должно достигаться или при t=0, или при x =0 илипри x=l.

Физический смысл этой теоремы очевиден и заключается в следующем. Если температура на границе или в начальный момент не превосходит некоторого значения M, то при отсутствии источников тепла внутри тела не может создаться температура, больше чем М.

Остановимся на доказательстве теоремы для максимального значения. Оно ведется от противного. Итак, пусть М – максимальное значение функции u(x,t) при t = 0 (0 ≤ x ≤ l) или при x = 0 илипри x = l (0 ≤ t ≤ T). Допустим теперь, что в некоторой точке области (x₀, t₀), такой, что 0 < x₀ < l и0 < t₀ ≤ T , функция u(x,t) достигает своего максимального значения, превосходящего М на величину ε, т.е.

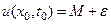
Тогда в точке (x₀, t₀) должны выполняться соотношения

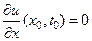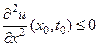и (41)

Далее так как u(x₀, t) достигает максимального значения при 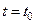, то

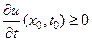, (42)

причем при всех значениях 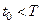будет выполняться знак равенства.

Далее найдем такую точку (x₁, t₁), в которо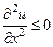й и 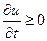. Для этого рассмотрим вспомогательную функцию

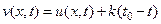, (43)

где k – постоянный коэффициент. Очевидно, что

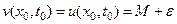
и

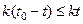
Выберем 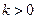так, чтобы kT было меньше ε/2, т.е. 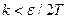, тогда максимальное значение v(x, t) при t = 0 (0 ≤ x ≤ l) или при x = 0 илипри x = l не будет превосходить 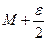, т.е.

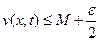(при t = 0 или x = 0 или x = l ), (44)

так как для этих аргументов первое слагаемое в формуле (43) не превосходит М, а второе .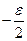

В силу непрерывности функции v(x, t), она должна в некоторой точке (x₁,t₁) достигать своего максимального значения, причем

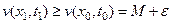
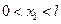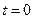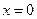Момент времени t₁ строго больше нуля и , так как при или , или 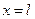имеет место неравенство (44). В точке (x₁, t₁), по аналогии с (41) и (42), должно быть

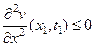и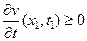

Имея в виду определение функции v (x, t) (43), получим

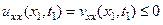
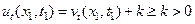
Отсюда следует, что

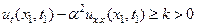
т.е. уравнение (40) во внутренней точке (x₁,t₁) не удовлетворяется. Тем самым доказано, что решение u(x,t) уравнения теплопроводности (40) внутри области не может принимать значений, превосходящих наибольшее значение u(x,t) на границе.

Аналогично может быть доказана и вторая часть теоремы для минимального значения.

Приведем и докажем следствия из принципа максимального значения:

Следствие 1. Если два решения уравнения (40) 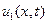и 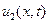удовлетворяют условиям:

,

,

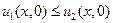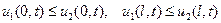то:

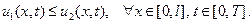
Доказательство. В силу линейности (40) функция 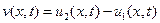является его решением, следовательно, удовлетворяет принципу максимального значения. При этом:

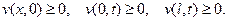
Следовательно:

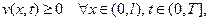
в противном случае 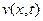имела бы отрицательное минимальное значение. Следствие 1 доказано.

Следствие 2. Если три решения уравнения (40) 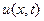, 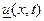и 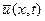удовлетворяют условию:

,

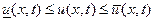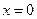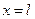при , и , то это же неравенство выполняются и для всех .

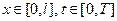Доказательство. Проводится просто применением следствия 1 к парам функц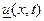ий 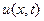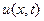и , и .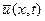

Следствие 3. Если для двух решений уравнения (40) 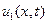и 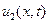имеет место неравенство:

,

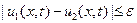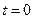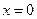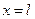при , и , то это же неравенство выполняются и для всех .

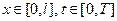Доказательство Проводится применением следствия 2 к следующим решениям уравнения (1): 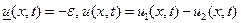и .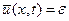

Замечание.

Покажем, что благодаря следствию 3 можно установить важнейшее свойство, обеспечивающее корректность постановки первой краевой задачи для (40), а именно непрерывную зависимость решения от начального и граничных условий.

Рассмотрим в решение уравнения (1), соответствующее начальному и граничным условиям вида:

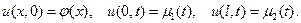
Пусть 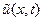есть решение уравнения (40), соответствующее возмущенным начальному и граничным условиям, задаваемыми функциям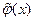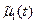и , и 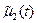, такими, что:

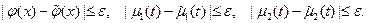
Используем следствие 3, можем заключить, что: 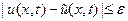, что и подразумевает сколь угодную близость решений исходной и возмущенной задач.