Применение метода разделения переменных

Мы в очередной раз воспользуемся методом разделения переменных в задаче о распространении тепла в ограниченном стержне длиной l (см.Рис.25) с теплоизолированной боковой поверхностью без внутренних источников тепла. В этом случае уравнение теплопроводности имеет простой вид:

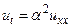(11)

Первоначальное распределение температуры по стержню задается начальным условием

(12)

Как мы помним, для успешной реализации метода разделения переменных граничные условия должны быть однородными. Будем считать, что на границах стержня поддерживается постоянная нулевая температура

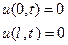(13)

Представим теперь искомую функцию 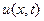в в идее произведения

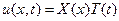(14)

Подставив это выражение в уравнение (26), получим

Разделим обе части на 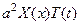, тогда уравнение примет вид

(15)

В отличие от применения этого метода для уравнения колебаний ограниченной струны мы обозначили константу разделения через λ², что не принципиально.

Соотношение (15) позволяет нам записать два уравнения:

(16)

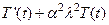(17)

Поскольку граничные условия нулевые, это приводит к тому, что и для функции X(x) могут (и должны) быть записаны нулевые граничные условия.

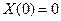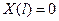и (18)

Решение задачи Штурма-Лиувилля для уравнения (16) с граничными условиями (18) нам уже знакомо, мы сразу можем записать найденные собственные числа и собственные функции. Итак, собственные функции имеют вид

, (n = 1,2,3,…)

где 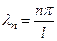, а 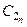– набор произвольных постоянных, которые пока не определены. Таким образом, имеем

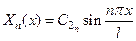, (19)

Обратившись теперь к уравнению (17) с известным уже набором значений λ_n мы придем к необходимости решать бесконечный набор уравнений одного вида

, (20)

где . Решение такого вида уравнений имеет вид

(21)

где A_n – произвольные постоянные.

Таким образом, для уравнения (14) мы можем записать весь набор решений

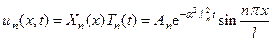(22)

При записи выражения (22) было учтено, что произведение произвольной константы C_2n на произвольную константу A_n будет также давать произвольную константу, которую можно снова обозначить через A_n. Как и в случае ограниченной струны (или стержня), каждая из функций X_n(x) представляет собой стоячую волну, а функция T_n – убывающая функция, стремящаяся к нулю при t стремящемся к бесконечности. Таким образом, и функции u_n(x,t) при t стремящемся к бесконечности стремятся к тождественному нулю.

Сумма всех решений (22) и будет общим решением уравнения (14)

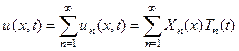(23)

Нам осталось определить константы A_n. Для этого, как и раньше, мы воспользуемся начальным условием. Подставляя решение (23) с учетом (22) в начальное условие (12), получим

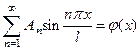
Воспользовавшись, как и в §6 Гл. II, свойством ортогональности системы функций sin(nπx), мы получим выражения для определения коэффициентов A_n

(24)

Следует отметить, что общее решение u(x,t) , как и каждая функция u_n(x,t), тоже стремится к тождественному нулю при t стремящемся к бесконечности. С физической точки зрения это означает, что первоначальное распределение температуры вдоль стержня со временем убывает до нуля, если на концах стержня поддерживается нулевая температура.

В заключении этого параграфа запишем решение нашей задачи полностью

При этом мы внесли под знак интеграла функцию , которая не зависит от ξ, а также операцию суммирования по n. Изменение порядков суммирования и интегрирования всегда законно при t >0 в силу того, что ряд в скобках сходится равномерно по ξ при t >0.

Обозначим выражение в квадратных скобках, которое зависит от переменных x, ξ, t через функцию G от этих переменных

(25)

Эта функция называется функцией мгновенного точечного источника или более подробно функцией температурного влияния мгновенного точечного источника тепла.

Физический смысл функции G(x, ξ, t) состоит в том, что она представляет собой температуру в точке x в момент времени t, вызванную действием мгновенного точечного источника мощностью сρ, помещенного в момент t = 0 в точке x = ξ если температура в начальный момент была равна нулю.