Задача Коши. Характеристики.

Запишем уравнение гиперболического типа в общем виде

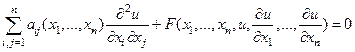, (1)

где a_ij – заданные вещественные функции в некоторой области D n-мерного пространства x₁,…, x_n. Не ограничивая общности, можно считать .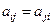

Пусть в области D задана достаточно гладкая (n – 1)-мерная поверхность S и в каждой точке этой поверхности некоторая линия l, не являющаяся касательной к поверхности и достаточно гладко изменяющаяся при движении по поверхности S. В частном случае это может быть нормаль.

Пусть, кроме того, на поверхности S заданы значения функции u(x₁,…, x_n) и её производной первого порядка по направлению l. Эти значения на поверхности S называются начальными данными Коши.

Теперь сформулируем задачу Коши для уравнения (1) следующим образом.

Найти решение уравнения (1) в некоторой окрестности поверхности S, удовлетворяющее на этой поверхности начальным данным Коши.

Заметим, что начальные данные Коши позволяют определить на поверхности S все частные производные первого порядка функции u (x₁,…, x_n). Что касается производных второго порядка на поверхности S, то для их определения в нашем распоряжении имеется начальные данные и уравнение (1) и нужно выяснить, когда уравнение (1) однозначно определяет вторые производные по начальным данным.

Сначала выясним это для начальных данных, заданных специальным образом, а именно на гиперплоскости :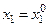

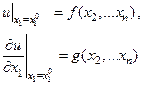(2)

При этом в качестве направления l выбрана нормаль. Начальные данные (2) дают нам возможность определить на гиперплоскости 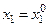все производные первого порядка и все производные второго порядка, кроме 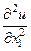. Для определения этой последней производной нам надо воспользоваться самим уравнением (1) , положив в нем 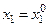. Причем, если 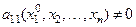, то мы однозначно определим производную 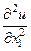на гиперплоскости 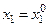. Если же 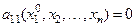, то мы либо получим тождество, либо придем к невозможности равенства.

Рассмотрим теперь общий случай, когда начальные данные заданы на поверхности S, которая определяется уравнением

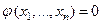(3)

Мы постараемся этот общий случай свести к только что рассмотренному путем выбора в окрестности поверхности S таких новых координат, в которых наша поверхность стала координатной. Для этого одну из новых координат, например ξ₁, выберем таким образом, чтобы на S она обращалась в нуль, т.е.

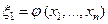, (4.а)

а остальные (n –1) координаты определим следующим образом

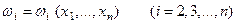, (4.б)

где функции ω _I достаточно гладкие, причем якобиан преобразования отличен от нуля на поверхности S. Запишем производные от функции u по x_i через производные по ξ _I :

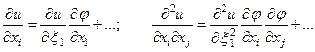
Подставив эти выражения в уравнение (1), мы вместо него получим

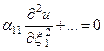(5)

где

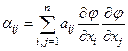(6)

В силу (3), (4.а) и (4.б) начальные данные задаются теперь на гиперплоскости 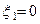, т.е. они имеют тот специальный вид, который мы рассмотрели предварительно, а значит, мы можем воспользоваться полученным при этом рассмотрении результатом.

В результате мы можем утверждать, что для того, чтобы решение задачи определения на поверхности S, т.е. при 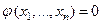, вторых производных функции u по начальным данным и уравнению (1) приводило к неопределенности или несовместности, необходимо и достаточно, чтобы функция 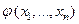удовлетворяла условию

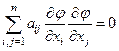(7)

Поверхность 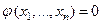называется характеристической поверхностью уравнения (1) или просто характеристикой, если в каждой точке этой поверхности имеет место равенство (7).

Следует обратить внимание на то, что функция φ в соответствии с определением характеристики должна удовлетворять условию (7) только на поверхности 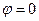. Если потребовать, чтобы условие (7) выполнялось не только на поверхности 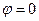, тогда условие (7) будет представлять собой уравнение в частных производных первого порядка. Тогда решение этого уравнения будет давать не одну характеристику, а целое семейство характеристик, определяемых равенством

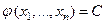, (8)

где С – произвольная постоянная.

С другой стороны, для того, чтобы уравнение (8) определяло семейство характеристик, необходимо и достаточно, чтобы функция 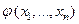удовлетворяла уравнению (7). Можно показать, что всякую характеристику уравнения (1) можно включить в семейство, имеющее вид (8) и что, таким образом, решения уравнения (7) определяют все характеристические поверхности.

Уравнение (7) называется уравнением характеристик дифференциального уравнения (1).

Рассмотрим для примера частный случай волнового уравнения

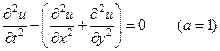(9)

и коническую поверхность в пространстве (x, y, t):

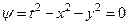
Уравнение (7) при этом будет иметь вид

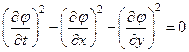(10)

При 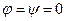это уравнение удовлетворяется. Действительно

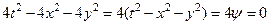
Отсюда следует, что конус 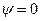является характеристической поверхностью уравнения (9). В то же время поверхности 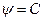при С ≠ 0 уже не является характеристическими. Тогда конус 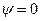можно включить в семейство конусов

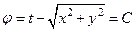
Определенное таким образом φ удовлетворяет уравнению (10) и, следовательно, все поверхности семейства 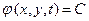являются характеристическими поверхностями уравнения (9).

Слабый разрыв. Фронт волны

Предположим, что существует решение уравнения (1) которое на некоторой поверхности S, задаваемой уравнением (3) для некоторых производных второго порядка имеет разрыв первого рода, причем само решение и его производные первого порядка остаются непрерывными при переходе через поверхность S. Будем рассматривать это решение по разные стороны от поверхности S как два различных решения уравнения (1). Эти решения на поверхности имеют одинаковые начальные данные, но различные значения производных второго порядка, т.е. существует неопределенность при нахождении вторых производных. Это означает, что поверхность S должна быть характеристической поверхностью уравнения (1).

К такому же выводу приводит предположение о том, что не только само решение и его частные производные первого порядка, но и частные производные второго порядка остаются непрерывными при переходе через поверхность S, а разрыв первого рода имеет место лишь для производных порядка выше второго.

И в первом и во втором случае говорят, что на поверхности S имеет место слабый разрыв. В общем случае говорят, что решение уравнения второго порядка (1) имеет слабый разрыв на поверхности S, если при переходе через эту поверхность само решение и его первые производные остаются непрерывными, а некоторые производные порядка выше первого имеют при этом разрыв первого рода.

Обратимся теперь к задачам математической физики, где одна из независимых переменных имеет физический смысл времени, при этом остальные переменные являются пространственными координатами. Иначе говоря, общее число независимых переменных будет равно 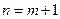, где m – число пространственных переменных. Решение уравнение (1) можно рассматривать как функцию точки в m-мерном пространстве R_m с координатами x₁,…, x_m, зависящую от времени как от параметра. Тогда вместо поверхности (3) будем иметь поверхность слабого разрыва

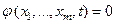, (11)

которая движется в m-мерном пространстве. В разрешенном виде (11) можно записать следующим образом

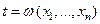(12)

и тогда

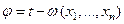(13)

Поверхность 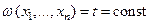называют фронтом волны, который перемещается с течением времени в направлении вектора grad ω. Чтобы определить величину этой скорости наряду с моментом времени t, в который пересечение нормали с поверхностью будет находиться в точке М,рассмотрим момент 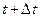. В этот момент времени фронт волны будет пересекать нормаль n в некоторой точке М₁, находящееся на расстоянии Δnот точки М. Предел отношения 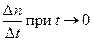и будет определять величину скорости движения фронта волны. Итак

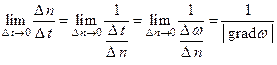(14)

и тогда вектор скорости движения фронта волны определяется формулой

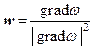(15)

В случае 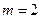будет линия на плоскости (x₁, x₂).

В качестве примера рассмотрим двухмерное волновое уравнение

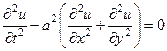
В этом случае уравнение (7) запишется следующим образом

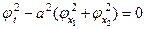(16)

Подставляя сюда правую часть уравнения (13) для двухмерного случая, получим

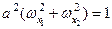
Поскольку выражение в скобках есть ничто иное, как grad ω, то

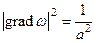
Следовательно, скорость движения фронта волны будет равна a.

Г л а в а V. Уравнения теплопроводности и диффузии