Решение задачи о колебаниях круглой мембраны
Мы будем решать задачу о колебаниях мембраны методом разделения переменных, который уже использовался нами при решении задачи о колебаниях струны. Для реализации этого метода было важно, чтобы граничные условия первого рода были нулевыми, т.е. концы струны были закреплены неподвижно. Кроме того, в одномерном случае (ограниченная струна или стержень), граница задается равенством единственной пространственной переменной константе (0 или l). Это также было важно при реализации метода.
В задаче о колебании мембраны также придется задать нулевое граничное условие первого рода. Однако уравнение границы на плоскости будет содержать две координаты, и это не позволит при разделении переменных перенести нулевые граничные условия на одну из координат. При выполнении определенных условий это можно сделать, но тогда само уравнение приобретает такой вид, что разделение переменных в нем оказывается под вопросом.
В связи с этим обычно решают задачу для круглой или прямоугольной мембраны. В этих случаях её границей является либо окружность, либо прямоугольник. В этих случаях задание границы сводится к приравниванию одной из переменных постоянной величине. Для круглой мембраны в полярной системе координат (r, φ) граничное условие сводятся к заданию смещения u при 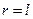 , где l – радиус окружности.Само уравнение нужно также записать в полярной системе координат. Тогда задача формулируется следующим образом.
, где l – радиус окружности.Само уравнение нужно также записать в полярной системе координат. Тогда задача формулируется следующим образом.
Найти решение однородного уравнения
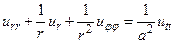 (58)
(58)
При начальных условиях
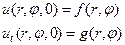 (59)
(59)
и при граничном условии
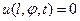 (60)
(60)
Метод разделения переменных осуществим в два этапа. На первом этапе отделим функцию, зависящую от времени, представив искомое решение в следующем виде


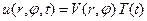 (61)
(61)
По аналогии с решением задачи о колебании струны можно предположить, что функция V(r,φ) будет определять форму колебания мембраны, а множитель T(t) – изменяющуюся во времени амплитуду этих колебаний.
Подставив представление (61) в исходное уравнение (58), получим
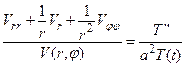 (62)
(62)
Как мы видим, левая часть этого равенства зависит от r и φ, а правая от t, а это возможно лишь, если та и другая равны константе, которую называют константой разделения. Она, как мы выяснили при решении задачи о колебании ограниченной струны, должна быть отрицательной, чтобы уравнение, которое мы получим разделения переменных для функции T, имело нетривиальное и ограниченное решение. В связи с этим её логично обозначить через –λ2 и переписать уравнение (62) следующим образом
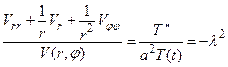 (63)
(63)
Из этого выражения получаем два уравнения. Одно из них известное уравнение гармонических колебаний
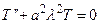 , (64)
, (64)
которое, как известно, имеет общее решение следующего вида
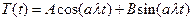 (65)
(65)
Второе уравнение, которое мы получим из соотношения (17) будет иметь вид
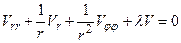 (66)
(66)
или
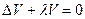 (67)
(67)
Это уравнение называют уравнением Гельмгольца. Оно играет важную роль в математической физике, поскольку к нему сводятся не только задачи о колебаниях, в том числе и в трехмерном случае, но и многие другие задачи (теплопроводности, диффузии и т.д.). Некоторые из них будут сформулированы в последующих главах.
Для уравнения (66) можно сформулировать граничное условие. Действительно, подставляя представление (61) в граничное условие (60), мы в качестве единственно возможного условия его выполнения получим
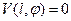 (68)
(68)
Таким образом, нахождение решения уравнения (66) при граничном условии (68), а также нахождение тех значений числа λ, при которых существует нетривиальное решение, представляет собой уже знакомую нам задачу Штурма-Лиувилля. Напомним, что искомые функции называют собственными функциями, а значения числа λ – собственными значениями задачи Штурма-Лиувилля.
Для функции V(r,φ) нужно сформулировать также требование периодичности по координате φ, т.е.
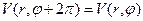 (69)
(69)
Теперь можем сделать следующий шаг и представить искомую функцию двух переменных V(r,φ) в виде произведения двух функций
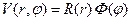 (70)
(70)
При этом условие (68) требует, чтобы функция Ф(φ) была периодической, а для функции R(r) после подстановки (70) в (67) получим нулевое граничное условие
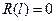 (71)
(71)
Теперь подставим выражение (70) в уравнение (66), разделив все его члены на RΦ и умножив их на r2 . В результате получим соотношение
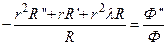 ,
,
обе части которого должны быть равны, как и на предыдущем шаге разделения переменных, постоянной отрицательной величине, т.е.
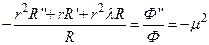 (72)
(72)
В результате получаем два уравнения. Одно из них относительно функции Ф(φ):
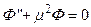 (73)
(73)
Нетривиальное периодическое решение этого уравнения существует лишь при 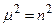 (где n – целое число). Иначе говоря, мы будем иметь бесконечный набор решений
(где n – целое число). Иначе говоря, мы будем иметь бесконечный набор решений
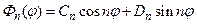 (74)
(74)
Второе уравнение, следующее из формулы (24), будет иметь вид
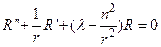 , (75)
, (75)
На самом деле, поскольку n – любое целое число, то мы будем иметь бесконечный набор уравнений одного вида. При этом предстоит найти и значение λ, которое для каждого n будет своё. Так что правильнее будет написать
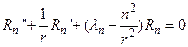 (76)
(76)
Их надо решить при выполнении граничного условия (71) и условия ограниченности функции R(r), в том числе в особой точке  , т.е.
, т.е.
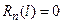 и
и 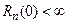 (77)
(77)
Уравнение (27) носит название уравнение Бесселя, записанное в полярных координатах.
Вводя новую переменную
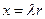
и обозначая
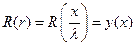
можем записать это уравнение в следующем более традиционном виде
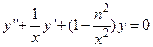 , (n =1,2,3,…) (78)
, (n =1,2,3,…) (78)
где 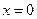 является особой точкой, c дополнительными условиями
является особой точкой, c дополнительными условиями
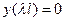 и
и 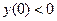 (79)
(79)
Решением уравнения Бесселя являются так называемые функции Бесселя. Это решение подробно излагается в курсе “Дополнительные главы математической физики”, а также в книгах [1], [3] и [6]. Здесь мы приведем лишь структуру решения, которое после учета второго условия (79) при обратном переходе к координате r имеет вид
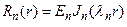 , (80)
, (80)
Граничные условия 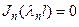 представляют собой бесконечный набор трансцендентных уравнений, каждое из которых в качестве решения дает возможность определить бесконечный набор значений
представляют собой бесконечный набор трансцендентных уравнений, каждое из которых в качестве решения дает возможность определить бесконечный набор значений 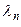 . Таким образом, у параметра
. Таким образом, у параметра 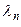 должен появиться второй индекс, который будет обозначать номер корня трансцендентного уравнения, т.е. мы получаем набор
должен появиться второй индекс, который будет обозначать номер корня трансцендентного уравнения, т.е. мы получаем набор 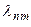 . Это означает, что и набор решений также будет иметь два индекса, а именно
. Это означает, что и набор решений также будет иметь два индекса, а именно

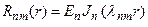 (81)
(81)
А поскольку функция T(t) по формуле (19) также зависит от 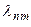 , то и она будет иметь два индекса –
, то и она будет иметь два индекса – 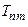 .
.
Таким образом, представив искомое решение в виде произведения функций
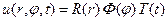 ,
,
мы нашли эти функции, решив соответствующие уравнения для каждой из них. При этом мы нашли бесконечный набор 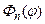 , а также двойные бесконечные наборы
, а также двойные бесконечные наборы 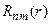 и
и 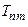 . Из этого следует, что мы будем иметь двойной бесконечный набор
. Из этого следует, что мы будем иметь двойной бесконечный набор 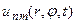 решений исходного уравнения (12). Каждое из них будет иметь следующий вид:
решений исходного уравнения (12). Каждое из них будет иметь следующий вид: 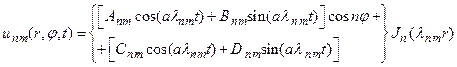 (82) Тогда общее решение получим в результате двойного суммирования
(82) Тогда общее решение получим в результате двойного суммирования
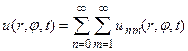
Коэффициенты 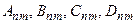 могут быть найдены в результате использования начальных условий (59) как коэффициенты разложения функций f (r, φ) и g (r, φ) в ряд по функциям Бесселя1).
могут быть найдены в результате использования начальных условий (59) как коэффициенты разложения функций f (r, φ) и g (r, φ) в ряд по функциям Бесселя1).
[1], [3] и [6].
1) См., например, Тихонов А. Н. Уравнения математической физики.–М.: Наука, 1972.
Г л а в аIV.Некоторые общие вопросы теории дифференциальных уравнений гиперболического типа
В этой главе мы рассмотрим ряд общих вопросов теории уравнений в частных производных гиперболического типа, отвлекаясь от их физического смысла. В частности мы не будем придавать одной из независимых переменных смысл времени и не будем выделять её среди прочих, как это мы делали в предыдущем изложении. Начнем с рассмотрения задачи Коши для общего вида этого типа уравнений.
