Уравнение малых поперечных колебаний струны
В математической физике струной называют тонкую нить, не оказывающую сопротивление изгибу, которая находится в состоянии натяжения. Выведем уравнение движения струны с этими свойствами с учетом действия внешней силы. Строго говоря, заранее мы не можем говорить, что это будет уравнение колебаний, поскольку только решение уравнения покажет нам, каким будет движение.
Расположим ось x вдоль линии натяжения бесконечной струны в состоянии равновесия, тогда перпендикулярная ей ось u будет параллельна поперечным смещениям этой струны (Рис. 5). Сила натяжения Т для всех точек струны будет одинакова по величине и направлена в каждой из этих точек по касательной к струне.

Рис. 5. Расположение струны и силы натяжения при отклонения от оси x.
Пусть ρ (x) – линейная плотность струны, а p(x,t) – удельная сила (в данном случае приходящаяся на единицу длины), приложенная перпендикулярно струне в ее исходном положении. Будем рассматривать поперечные смещения струны и считать их настолько малыми, что можно будет отбрасывать величины второго порядка малости по сравнению с 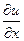 . В этом случае элемент струны dx после отклонения от положения равновесия будет иметь длину
. В этом случае элемент струны dx после отклонения от положения равновесия будет иметь длину
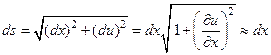 . (2)
. (2)
Это означает, при принятой нами степени малости поперечных смещений струны она не будет растягиваться и, следовательно, не будут возникать упругие силы.
Какая же сила будет стремиться возвратить каждую точку струны в положение равновесия? Дело в том, что при отклонении от положения равновесия в каждой точке будет появляться составляющая вектора Т по оси u, абсолютная величина которой будет равна будет равна T sin α . Это и будет сила, под действием которой точки струны будут стремиться вернуться в положение равновесия.
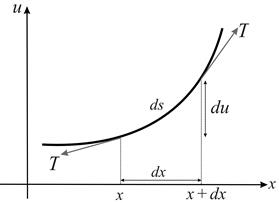
Рис. 6. К выводу уравнения колебаний струны
Посчитаем теперь сумму проекций всех сил, приложенных к элементу струны ds, на ось u (Рис. 6). Проекция силы Т на ось u будет равна:
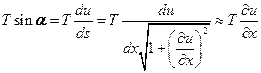 .
.
А равнодействующая сил, приложенных на концах элемента ds, составит:
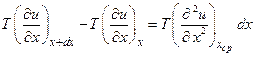 .
.
Сила, приложенная к элементу ds, будет равна p(x,t)dx. По второму закону Ньютона сумма приведенных выше сил должна быть равна массе элемента ds= ρ(x)dx, умноженной на его ускорение 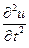 , т.е.
, т.е.
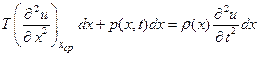 .
.
Разделив все члены этого уравнения на ρ и на dx, устремляя одновременно dx к нулю, мы и получим уравнение колебания струны:
 . (3)
. (3)
В случае, если ρ – величина постоянная, то можно ввести величину  , тогда уравнение (3) примет вид:
, тогда уравнение (3) примет вид:
 (4)
(4)
или:
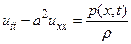 . (4.a)
. (4.a)
Обозначив  через F(x,t) можем переписать это уравнение следующим образом:
через F(x,t) можем переписать это уравнение следующим образом:
 . (4.б)
. (4.б)
Это и есть уравнение малых поперечных колебаний струны, хотя как мы уже говорили, правильнее было бы называть его уравнением модели струны.
При отсутствии внешней силы это уравнение будет иметь вид:
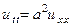 , (5)
, (5)
Это уравнение является уравнением свободных колебаний струны и отражает простой факт пропорциональности вертикального ускорения в каждой точке струны utt её вогнутости в этой точке uxx с коэффициентом пропорциональности a2.
Начальные условия
В случае бесконечной струны нужно сформулировать только начальные условия в следующем виде:
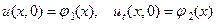 . (6)
. (6)
С физической точки зрения первое из этих условий задает смещение каждой точки струны, а второе – скорость каждой точки струны в начальный момент времени. Задача отыскания решения уравнения (4) или (5) при выполнении условий (6) называют задачей Коши.
Случай ограниченной струны.
Рассмотрим теперь струну длины l. Для ограниченной струны наряду с начальными условиями надо сформулировать и граничные условия. Существует три основных типа граничных условий.
Граничные условия I рода. В этом случае задаются перемещения на концах струны как функции времени (Рис. 7)
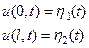 (7)
(7)
|
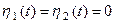 . Такие условия называют однородными, а само неподвижное закрепление – защемлением.
. Такие условия называют однородными, а само неподвижное закрепление – защемлением. | |
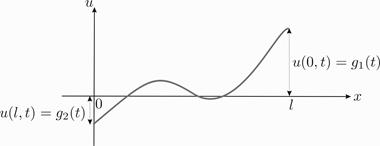
Рис. 7. Граничные условия первого рода
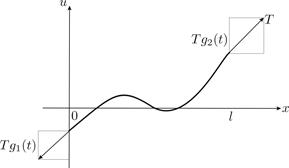
Рис. 8. Граничные условия второго рода
Граничные условия II рода. В этом случае задаются проекции силы на ось u на концах струны как функции времени. Как мы выяснили, каждая из них равна 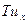 , поэтому на концах задаются производные ux как функции времени (Рис. 8)
, поэтому на концах задаются производные ux как функции времени (Рис. 8)
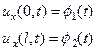 (8)
(8)
Если концы струны свободны, хотя и перемещаются только по вертикали, то в условиях (7) g1(t) и g2(t) будут равны нулю.
Граничные условия III рода. В этом случае лучше начать с механического смысла этих условий. Сначала предположим, что концы струны связаны с осью x (см.рис.13), тогда со стороны каждой из пружин на концы струны по закону Гука будут действовать силы пропорциональные смещению u. Поскольку силы, действующие со стороны пружин должны быть равны вертикальным проекциям сил со стороны струны, то можно записать условия на концах следующим образом:
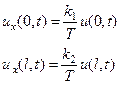 , (9)
, (9)
где k1 и k2 – жесткости пружин, прикрепленных к струне на концах струны. Такое граничное условие часто называют упругим закреплением струны в граничных точках
Теперь рассмотрим общий случай, когда один конец пружины прикреплен к струне, а второй движется по вертикали по заданному закону времени θ (t) (Рис. 9). Тогда условия (9) изменятся следующим образом:
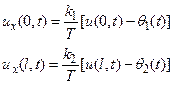 (10)
(10)
После переноса слагаемых и переобозначений мы получим граничные условия III рода в традиционном виде
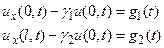 (11)
(11)
где 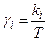 ,
, 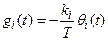 (i =1,2)
(i =1,2)
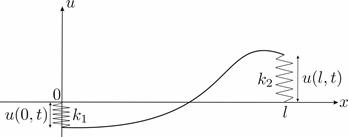
Рис. 9. Граничные условия третьего рода (частный случай).
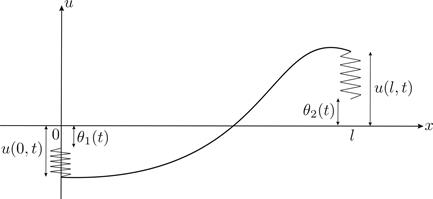
Рис. 10. Граничные условия третьего рода (общий случай).
К перечисленным видам граничных условий нужно добавить граничное условие, которое описывает действие на конце струны вертикальной силы, пропорциональной скорости и направленной в противоположном направлении. Такую силу обычно называют силой вязкого трения. Она может создаваться гидравлическим демпфером, соединяющим конец пружины с неподвижной точкой на оси x. Условие такого типа записывается (для левого конца) следующим образом:
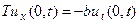 (12)
(12)
или 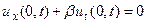 , где
, где 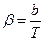 (13)
(13)
В некоторых физических задачах приходится прибегать к использованию на разных концах струны разных типов граничных условий. Например, на левом конце задается условие защемления, а на правом упругое закрепление.
Решение задачи Коши
Формула Даламбера
Чтобы выяснить, как будет вести себя бесконечная струна в отсутствии внешних сил, необходимо решить задачу Коши для уравнения (5) с начальными условиями (6), которые мы перепишем в следующем виде:
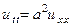 , (14)
, (14)
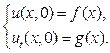 , (15)
, (15)
Одно из условий (15) может быть нулевым, но не оба, ибо в этом случае струна будет оставаться в исходном, недеформированном состоянии.
Решение задачи Коши осуществим в три этапа:
1-й шаг (приведение уравнения (7) к каноническому виду):
Введем новые переменные ξ и η следующим образом:
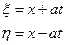 (16)
(16)
и запишем равнение (14) в новых переменных. Для этого получим выражения для uxx и utt:
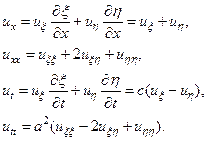
После подстановки полученных выражений в исходное уравнение (14) получим:
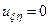 . (17)
. (17)
Уравнение (17) является каноническим видом уравнения (14), а переменные ξ и η – каноническими переменными.
2-й шаг (решение преобразованного уравнения):
Проинтегрируем полученное уравнение по ξ, а затем по η. После интегрирования по ξ, получим:
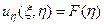 ,
,
где F(η) – произвольная функция от η.
После интегрирования по η получим
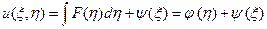 ,
,
где φ(η) и ψ(ξ) – произвольные функции своих аргументов.
3-й шаг:
Возвращаясь к старым переменным, получим

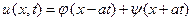 . (18)
. (18)
Физический смысл полученного решения состоит в том, что оно представляет собой суперпозицию двух волн, распространяющихся вдоль оси x в противоположных направлениях со скоростью a, как это показано на рис.11, причем формы этих волн, определяемые функциями 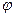 и ψ, являются произвольными.
и ψ, являются произвольными.
4-й шаг (Использование начальных условий):
Для конкретизации формы воспользуемся начальными условиями. Для этого подставим полученное решение и его производную по времени в начальные условия (15).
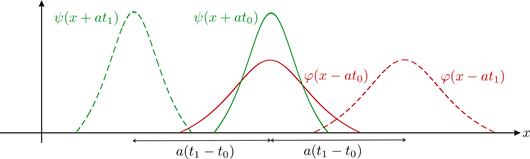
Рис. 11. Распространяющиеся волны
В результате получим два уравнения относительно неизвестных функций φ(x) и ψ(x):
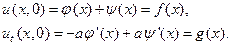
Проинтегрировав второе уравнение от x0 до x, получим систему уравнений относительно искомых функций:
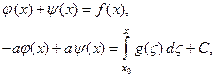
где С – произвольная константа. Решая эту систему, получим:
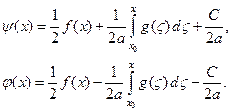
Записывая полученные решения для любого времени t, будем иметь
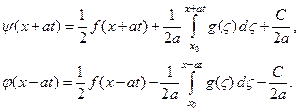
Складывая почленно оба выражения с одновременным изменением порядка интегрирования во втором из них, получим окончательный вид решения задачи Коши:
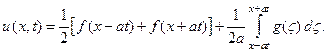 (19)
(19)
Эта формула носит название формулы Даламбера. Она была получена в предположении, что решение поставленной задачи Коши существует, а её наличие доказывает и единственность решения. Можно показать и непрерывную зависимость решения от начальных данных. В самом деле, для любого ε > 0 можно указать такое δ > 0, что если заменить f и g на f1 и g1,так, что
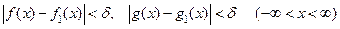 ,
,
то разность между первоначальным решением u (x,t) и новым решением u1 (x,t) будет по абсолютной величине меньше ε на любом конечном отрезке времени, что легко следует из формулы (19).
Частные случаи
Рассмотрим два частных случая начальных условий.
1) Н а ч а л ь н ы е с к о р о с т и т о ч е к с т р у н ы р а в н ы н у л ю, а начальное смещение имеет место лишь в конечном промежутке (– b, b). В этом случае формула (19) будет иметь вид:
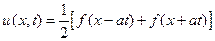 . (20)
. (20)
Решение (20) представляет собой сумму двух волн, распространяющихся влево и вправо со скоростью a, причем начальная форма обеих волн определяется функцией f(x)/2, т.е. равной половине первоначального смещения струны.
Пусть, в частности, начальное смещение неограниченной струны, материал которой таков, что 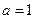 , задается следующим образом:
, задается следующим образом:
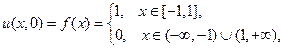
Тогда, пользуясь формулой (20), мы можем выписать выражения для смещения струны в моменты времени 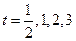 .
.
Для 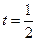 мы получим:
мы получим:
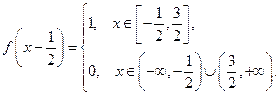
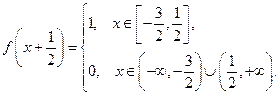
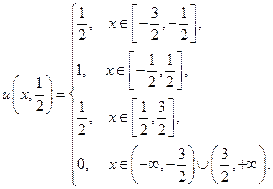
Для 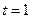 :
:
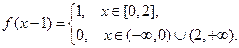
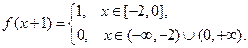
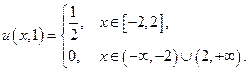
Для 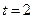 :
:
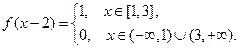
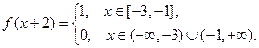
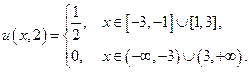
Для 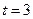 :
:
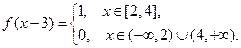
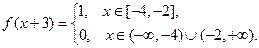
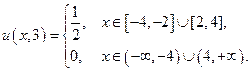
2) Н а ч а л ь н о е с м е щ е н и е р а в н о н у л ю, а функция g(x) отлична от нуля лишь в ограниченном промежутке (– b, b). В этом случае говорят, что струна имеет только начальный импульс, арешение (19) принимает вид:
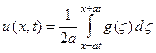 , (21)
, (21)
или полагая:
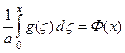 ,
,
можем записать:
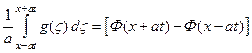 .
.
Тогда окончательно получим:
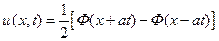 . (22)
. (22)
Отсюда видно, что и в этом случае по струне будут распространяться две волны – одна прямая и одна обратная. Результат их прохождения будет следующим. При 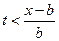 промежуток интегрирования в формуле (21) не будет иметь общих точек с интервалом (– b, b), а значит функция g(x) будет равна нулю (струна покоится). Начиная с момента времени
промежуток интегрирования в формуле (21) не будет иметь общих точек с интервалом (– b, b), а значит функция g(x) будет равна нулю (струна покоится). Начиная с момента времени 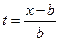 промежуток интегрирования в формуле (21) будет накладываться на интервал (– b, b) и точка x начнет смещаться. Наконец, при
промежуток интегрирования в формуле (21) будет накладываться на интервал (– b, b) и точка x начнет смещаться. Наконец, при 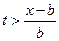 промежуток интегрирования будет целиком содержать интервал (–b, b) и интегрирование будет сводиться к интегрированию по этому интервалу, так как вне его g(x) = 0, т.е. при
промежуток интегрирования будет целиком содержать интервал (–b, b) и интегрирование будет сводиться к интегрированию по этому интервалу, так как вне его g(x) = 0, т.е. при 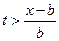 смещение u (x, t) будет иметь постоянное значение d, определяемое интегралом:
смещение u (x, t) будет иметь постоянное значение d, определяемое интегралом:
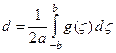 .
.
Таким образом, действие первоначального импульса приводит к тому, что с течением времени точки струны смещаются на отрезок d и остаются без движения в этом новом положении. Иначе говоря, волны оставляют после себя постоянный след своего прохождения.
Пусть, в частности, начальное смещение неограниченной струны равно нулю, а начальная скорость задается следующим образом:
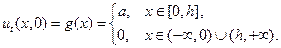
Тогда, пользуясь формулой (21) и (22), мы можем выписать выражения для смещения струны в любой момент времени.
Имея в виду, что интеграл с переменным верхним пределом от заданной функции 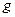 определяется выражением
определяется выражением
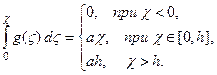
для 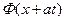 и
и 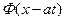 получим:
получим:
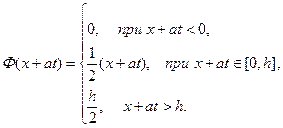
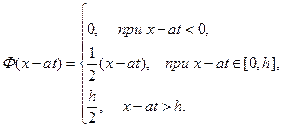
В частности, для 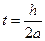 :
:
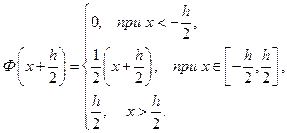
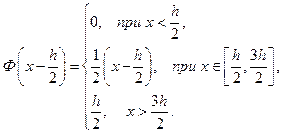
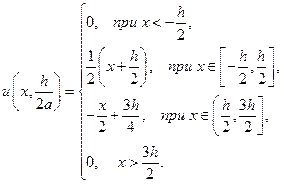
Для 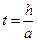 :
:
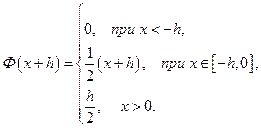
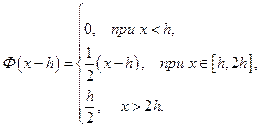
и тогда
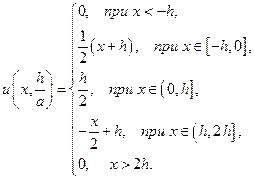
Для 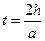 :
:
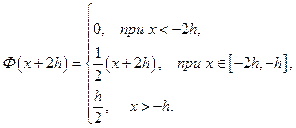
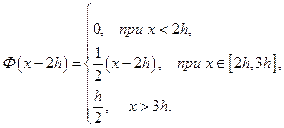
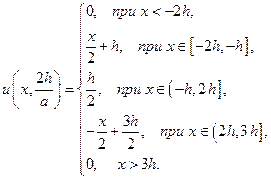
Графическая интерпретация
Первый частный случай имеет простую графическую интерпретацию. На рис. 12. показано, как начальное смещение расщепляется на две полуволны, движущиеся в противоположных направлениях.
Приведенная схема может служить графическим способом построения решения задачи Коши с нулевой начальной скоростью.
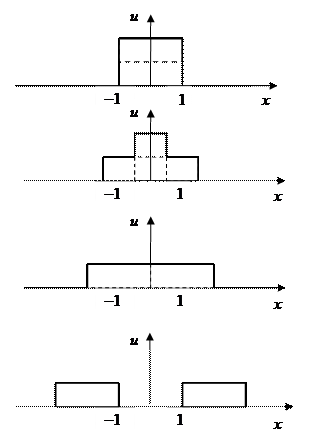
Рис. 12. Графическая иллюстрация первого частного случая.
Для второго частного случая на рис. 14 приведены графики полученного смещения в случае 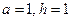 в моменты времени
в моменты времени 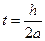 и
и 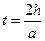
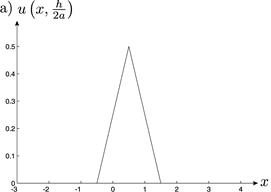
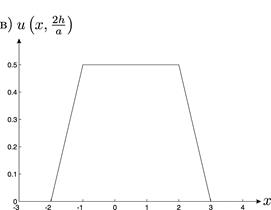
Рис. 13. Графическая иллюстрация второго частного случая.
Метод характеристик
Ещё один способ решения задачи Коши можно получить исходя из пространственно-временной интерпретации формулы Даламбера. Сначала рассмотрим 1-й частный случай, когда начальная скорость точек струны равна нулю. В этом случае решение определяется формулой (20)
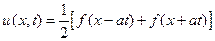
Из этой формулы следует, что функция f остается постоянной, если сохраняют свое значение выражения x – at или 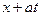 , т.е.
, т.е. 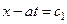 ,
, 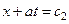 . На плоскости (x, t) эти выражения представляют собой уравнения прямых, называемых характеристиками волнового уравнения (Рис. 14).
. На плоскости (x, t) эти выражения представляют собой уравнения прямых, называемых характеристиками волнового уравнения (Рис. 14).
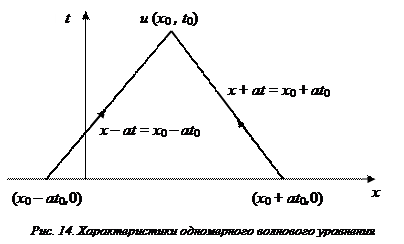
Вдоль указанных прямых функция f сохраняет своё значение, которое она имела на оси x т.е. в начальный момент времени, а совокупность этих значений нам известна как начальное смещение струны. Таким образом, решение задачи Коши для уравнения колебания струны для любой точки плоскости (x, t) можно получить, проведя через неё две характеристики, уравнения которых будут
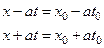
и взяв полусумму значений функции f, которые она имеет на этих характеристиках.
Используя такую интерпретацию формулы Даламбера, решим задачу, сформулированную в предыдущем параграфе, а именно
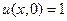 в интервале
в интервале 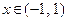 и 0 во всех остальных точках
и 0 во всех остальных точках
ut(x,0) = 0
На рис. 15 решение задачи изображено в плоскости переменных x, t , а не u, x как в предыдущем параграфе. Всё полупространство получается разбитым на 6 областей. В трех из них решение равно нулю, в двух – одной второй и в одной – единице.
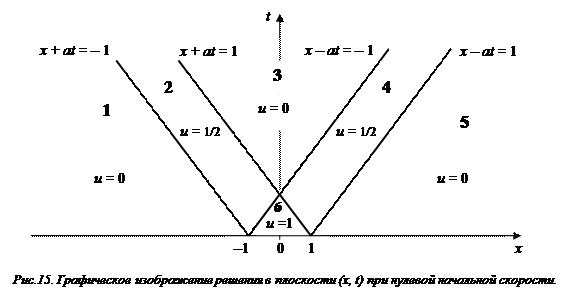
Теперь перейдем к случаю, когда начальное смещение равно нулю, а начальная скорость является произвольной функцией координаты g (x). В этом случае решение имеет вид (15).
Значение величины u в каждой точке(x0, t0) можно интерпретировать как интеграл от начальной скорости в пределах от 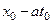 до
до 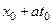 , т.е.
, т.е.
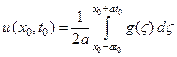 (23)
(23)
В качестве примера построим решение задачи Коши в координатах x,t с начальными условиями
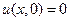
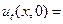
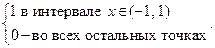
Подставляя в формулу (23) в каждой из шести областей (см. Рис.15) свои значения функции g(ζ) и свои пределы интегрирования, получим
В областях 1 и 5 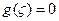 и следовательно
и следовательно 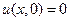 ; в остальных областях
; в остальных областях 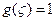 , при этом
, при этом
в области 2 пределы интегрирования от – 1 до 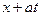 и
и 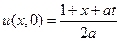 ,
,
в области 3 пределы интегрирования от + 1 до –1 и 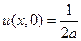 ,
,
в области 4 пределы интегрирования от 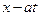 до 1 и
до 1 и 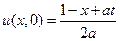 ,
,
в области 6 пределы интегрирования от 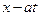 до
до 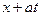 и
и 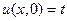 .
.
С физической точки зрения рассматриваемый процесс можно пояснить следующим образом. Пусть точка x лежит правее промежутка (– 1, 1). При t = 0 промежуток интегрирования ( 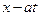 ,
, 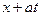 ) вырождается в точку x, а затем при увеличении t он расширяется в обе стороны со скоростью a. При
) вырождается в точку x, а затем при увеличении t он расширяется в обе стороны со скоростью a. При 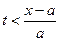 этот промежуток будет находиться вне промежутка (– 1, 1) и функция g (x) в нем будет равна нулю, а значит и u(x, t) = 0, т.е. точка x покоится. Начиная с момента времени
этот промежуток будет находиться вне промежутка (– 1, 1) и функция g (x) в нем будет равна нулю, а значит и u(x, t) = 0, т.е. точка x покоится. Начиная с момента времени 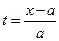 промежуток (
промежуток ( 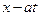 ,
, 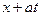 ) будет покрывать интервал (– 1, 1) , в котором в котором функция g (x) равна единице и точка x начнет перемещаться по мере прохождения фронта волны через точку x. Наконец, при
) будет покрывать интервал (– 1, 1) , в котором в котором функция g (x) равна единице и точка x начнет перемещаться по мере прохождения фронта волны через точку x. Наконец, при 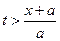 промежуток (
промежуток ( 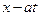 ,
, 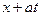 ) будет целиком содержать интервал (– 1, 1) и интегрирование будет сводиться к интегрированию в этом интервале, т.е. при
) будет целиком содержать интервал (– 1, 1) и интегрирование будет сводиться к интегрированию в этом интервале, т.е. при 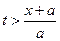 смещение токи x будет оставаться постоянным и равным 1/a. Момент времени
смещение токи x будет оставаться постоянным и равным 1/a. Момент времени 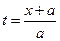 является моментом прохождения заднего фронта волны через точку x.
является моментом прохождения заднего фронта волны через точку x.
Этот процесс схематично проиллюстрирован на рис. 16. Таким образом, действие начального импульса приводит к тому, что с течением времени точки струны перемещаются на отрезок длиной u=1/a и остаются без движения в этом новом положении. Иначе говоря, волна оставляет после себя след своего прохождения. В результате положения u=1/a сначала достигает точка с координатой x=0, после чего область смещения постепенно распространяется на всю длину бесконечной струны.
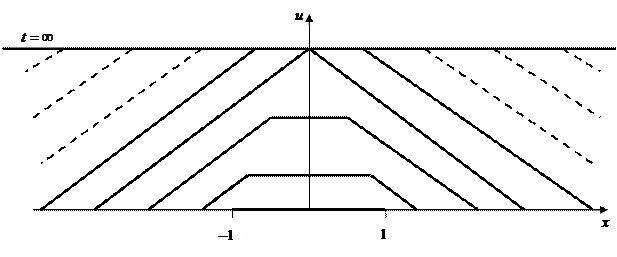
Рис. 16. Графическое изображение решения в плоскости (x, t) при нулевом начальном смещении.
