Тема: «Неопределенный и определенный интегралы. Применение определенного интеграла к решению прикладных задач. Дифференциальные уравнения »
Знания:
- определение первообразной функции;
- определение неопределенного интеграла;
- свойства неопределенного интеграла;
- таблицу неопределенных интегралов;
- методы интегрирования;
- свойства определенного интеграла;
- формулу Ньютона-Лейбница для вычисления определенных интегралов;
- основные понятия теории дифференциальных уравнений.
Умения:
- находить неопределенный интеграл различными методами;
- применять формулу Ньютона-Лейбница для вычисления определенного интеграла;
- находить общее и частное решение дифференциальных уравнений.
Задание 1
Вычислить следующие интегралы.
а) 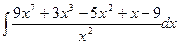 , б)
, б) 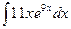 , в)
, в) 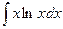 ,
,
г) 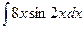 , д)
, д) 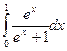 , е)
, е) 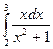 .
.
Решение.
а) 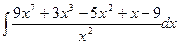
Для вычисления данного неопределенного интеграла применим метод непосредственного интегрирования. Преобразуем подынтегральное выражение и применим свойства неопределенного интеграла.
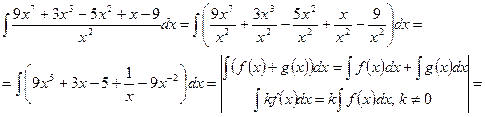
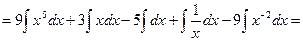
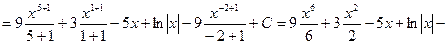
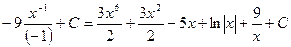
б) 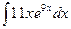
Для вычисления данного неопределенного интеграла применим метод интегрирования по частям. Согласно данного метода подынтегральное выражение следует разбить на две части : функцию 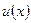 и дифференциал –
и дифференциал – 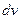 .
.
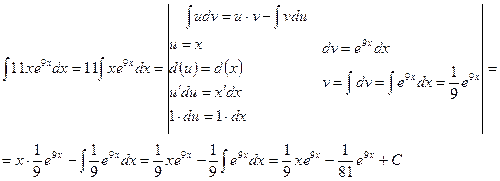
в) 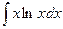
Для вычисления данного неопределенного интеграла применим метод интегрирования по частям. Согласно данному методу подынтегральное выражение следует разбить на две части: функцию 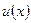 и дифференциал –
и дифференциал – 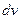 .
.
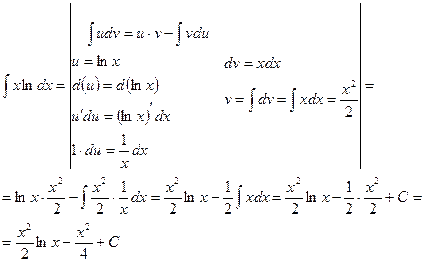
г) 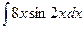
Для вычисления данного неопределенного интеграла применим метод интегрирования по частям. Согласно данному методу подынтегральное выражение следует разбить на две части: функцию 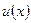 и дифференциал –
и дифференциал – 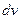 .
.
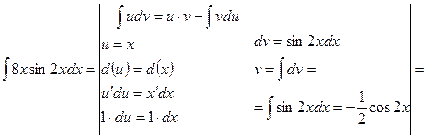
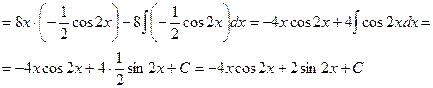
д) 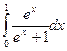
Для вычисления данного определенного интеграла применим метод подстановки. Согласно данному методу, необходимо ввести новую переменную так, чтобы свести подынтегральное выражение к одному из табличных интегралов, при этом обязательно произвести пересчет пределов интегрирования.
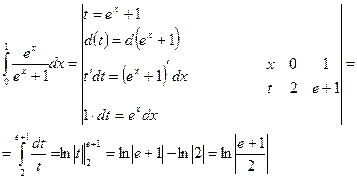
е) 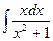
Для вычисления данного определенного интеграла применим метод подстановки. Согласно данному методу, необходимо ввести новую переменную так, чтобы свести подынтегральное выражение к одному из табличных интегралов, при этом обязательно произвести пересчет пределов интегрирования.
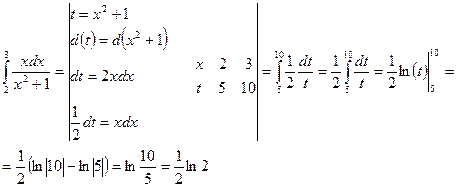
Задание 2.
а) Вычислить площадь фигуры, ограниченной линиями: 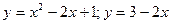 .
.
Решение.
Построим фигуру, площадь которой требуется найти (рис.1).
Графиком функции 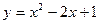 является парабола, ветви которой направлены вверх, так как
является парабола, ветви которой направлены вверх, так как 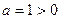 , а вершина находится в точке
, а вершина находится в точке 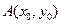 , где
, где
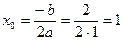 ;
; 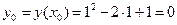 .
.
Таким образом, 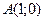 .
.
Найдём точки пересечения параболы с осью 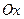 :
:
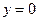 ;
; 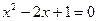 ;
;
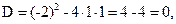
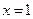 .
.
Парабола пересекает ось абсцисс в точках 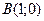 .
.
Для построения прямой, заданной уравнением 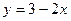 , достаточно указать координаты двух её точек:
, достаточно указать координаты двух её точек:
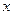 | 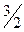 | |
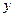 |
Найдём точку пересечения прямой и параболы. Для этого решим совместно систему уравнений:
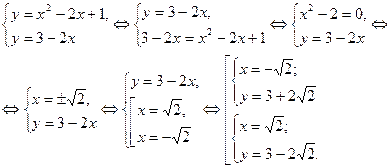
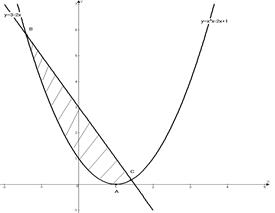
Рис. 1
Итак, прямая пересекает параболу в точках 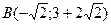 и
и 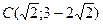 .Площадь заштрихованной фигуры
.Площадь заштрихованной фигуры 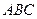 найдём по формуле
найдём по формуле
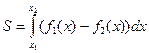 ,
,
где
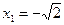 ,
, 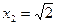 ,
, 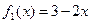 ,
, 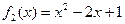 ,
,
так как прямая является верхней границей заштрихованной области, а парабола − нижней.
Итак,
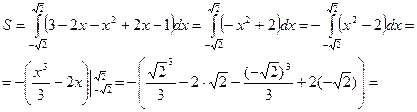
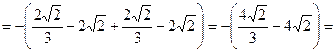
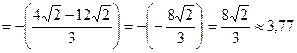 кв. ед.
кв. ед.
Ответ:Площадь фигуры, ограниченной линиями 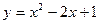 и
и 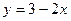 , равна
, равна 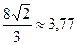 кв. ед.
кв. ед.
б) Вычислить объём тела, образованного вращением вокруг оси 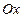 фигуры, ограниченной линиями:
фигуры, ограниченной линиями: 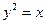 ,
, 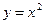 .
.
Решение.
Построим данные линии в системе координат:
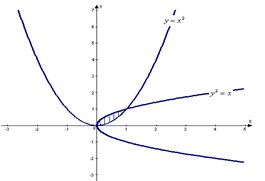
Рис. 2
Объём тела, образованного вращением вокруг оси 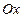 фигуры, ограниченной кривой
фигуры, ограниченной кривой 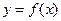 , определяется по формуле:
, определяется по формуле:
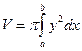 ,
,
Выразим 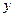 через
через 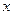 в уравнениях заданных кривых:
в уравнениях заданных кривых:
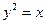 ,
, 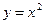 . Решая систему уравнений
. Решая систему уравнений 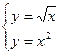 получим пределы интегрирования
получим пределы интегрирования 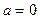 и
и 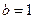 .
.
Тогда
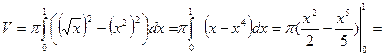
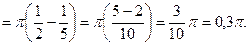 куб. ед.
куб. ед.
Ответ:Объём тела, образованного вращением вокруг оси 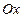 фигуры, ограниченной линиями
фигуры, ограниченной линиями 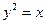 ,
, 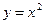 равен 0,3
равен 0,3 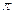 куб. ед.
куб. ед.
в) Вычислить объём тела, образованного вращением вокруг оси 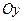 фигуры, ограниченной линиями:
фигуры, ограниченной линиями: 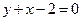 и
и 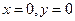 .
.
Решение.
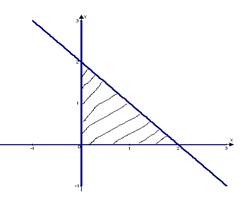
Рис.3
Объём тела, образованного вращением вокруг оси 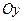 фигуры, ограниченной кривой
фигуры, ограниченной кривой 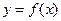 , определяется по формуле:
, определяется по формуле:
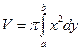 ,
,
где 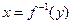 .
.
Выразим 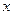 через
через 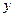 в уравнениях заданных кривых:
в уравнениях заданных кривых:
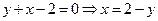 .
.
Пределы интегрирования 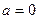 и
и 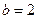 найдём, решив систему уравнений:
найдём, решив систему уравнений:
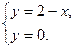
Тогда
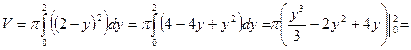

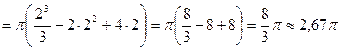 куб. ед.
куб. ед.
Ответ:Объём тела, образованного вращением вокруг оси 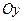 фигуры, ограниченной линиями
фигуры, ограниченной линиями 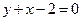 и
и 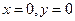 , равен
, равен 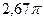 куб. ед
куб. ед
г) Какую работу нужно затратить, чтобы растянуть пружину на 0,1 м, если сила 200 Н растягивает пружину на 0,05 м?
Решение.
По закону Гука упругая сила, растягивающая пружину, пропорциональна этому растяжению 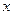 , т. е.
, т. е. 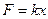 , где
, где 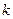 — коэффициент пропорциональности. Согласно условию задачи, сила
— коэффициент пропорциональности. Согласно условию задачи, сила 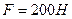 растягивает пружину на
растягивает пружину на 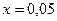 м; следовательно,
м; следовательно, 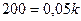 , откуда
, откуда 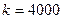 Искомая работа на основании формулы
Искомая работа на основании формулы 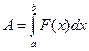 равна
равна
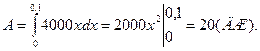
д) Найти путь, пройденный телом за 5 секунд от начала движения, если скорость тела 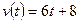 (м/с).
(м/с).
Решение.
Если 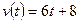 (м/с), то путь, пройденный телом от начала движения (
(м/с), то путь, пройденный телом от начала движения ( 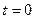 ) до конца 5-й секунды, равен
) до конца 5-й секунды, равен
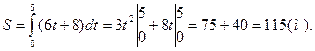
Задание 3
Найти общее решение дифференциального уравнения первого порядка
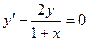 .
.
Решение.
Разделив в этом уравнении переменные и интегрируя обе части, получим
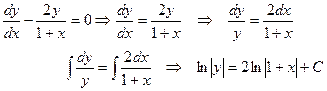
Задание 4
Найти общее и частное решение дифференциального уравнения
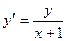 ,
, 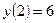 .
.
Решение.
Прежде чем найти частное решение данного дифференциального уравнения , найдем общее решение. Для этого представим производную функции 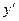 в виде частного аргумента
в виде частного аргумента 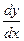 . Получим
. Получим
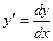
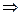
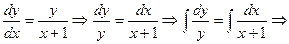
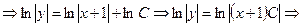
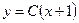 –общее решение
–общее решение
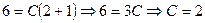
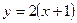 –частное решение
–частное решение
Приднестровский государственный университет
им. Т.Г. Шевченко
Физико-математический факультет
Кафедра «Алгебры, геометрии и методики преподавания математики»
Лабораторная работа №5
Вариант №___
