Сравнение двух дисперсий нормальных генеральных совокупностей

Пусть генеральные совокупности Х и Y распределены нормально. По независимым выборкам с объемами, соответственно равными n₁ и n₂, извлеченным из этих совокупностей, найдены исправленные выборочные дисперси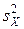и и 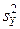. Требуется по исправленным дисперсиям при заданном уровне значимости a проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

Н₀: D(X)=D(Y).

Поскольку исправленные выборочные дисперсии являются несмещенными оценками генеральных дисперсий (см. 6.1.4.), то проверка данной гипотезы дает ответ на вопрос: значимо (существенно) или незначимо различаются исправленные дисперсии. Если окажется, что нулевая гипотеза справедлива, т.е. генеральные дисперсии одинаковы, то различие исправленных дисперсий незначительно и объясняется случайными причинами, в частности, случайным отбором объектов выборки. Если нулевая гипотеза отвергнута, т.е. генеральные дисперсии неодинаковы, то различие исправленных дисперсий значимо и не может быть объяснено случайными причинами, а является следствием того, что сами генеральные дисперсии различны.

На практике задача сравнения дисперсий возникает, если требуется сравнить точность приборов, самих методов измерения и т.д. Так, например, если различие исправленных выборочных дисперсий незначимо, то приборы имеют одинаковую точность. Если же их различие значимо, то точность измерений различна.

Случай 1. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу Н₀: D(X)=D(Y) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе Н₁: D(X)>D(Y), надо

1. Вычислить наблюдаемое значение критерия, равное отношению большей исправленной дисперсии к меньшей:

F_набл= .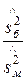

2. По таблице критических точек распределения Фишера-Снедекора (приложение 8), по заданному уровню значимости a и числам степеней свободы k₁=n₁–1 и k₂=n₂–1 (k₁ – число степеней свободы большей исправленной дисперсии, k₂ – меньшей исправленной дисперсии) найти критическую точку F_кр(a, k₁, k₂).

3. Если F_набл<F_кр – нет оснований отвергнуть нулевую гипотезу.

Если F_набл>F_кр – нулевую гипотезу отвергают.

Пример 6.2.4. По двум независимым выборкам объемов n₁=12 и n₂=15, извлеченным из нормальных генеральных совокупностей Х и Y, найдены исправленные выборочные дисперсии 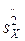=11,41 и 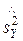=6,52. На уровне значимости 0,05 проверить нулевую гипотезу Н₀: D(X)=D(Y) о равенстве генеральных дисперсий при конкурирующей гипотезе Н₁: D(X)>D(Y).

○ Найдем отношение большей исправленной дисперсии к меньшей:

F_набл= 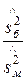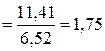. Конкурирующая гипотеза имеет вид Н₁: D(X)>D(Y), поэтому критическая область – правосторонняя.

По таблице приложения 8, по уровню значимости a=0,05 и числам степеней свободы k₁=12–1=11 и k₂=15–1=14 находим критическую точку F_кр(0,05, 11, 14)=2,56.

Так как F_набл<F_кр – нет оснований отвергнуть нулевую гипотезу о равенстве генеральных дисперсий. ●

Случай 2. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу Н₀: D(X)=D(Y) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе Н₁: D(X)¹D(Y), надо

1. Вычислить наблюдаемое значение критерия, равное отношению большей исправленной дисперсии к меньшей:

F_набл= .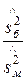

2. По таблице критических точек распределения Фишера–Снедекора (приложение 8), по заданному уровню значимости 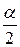(вдвое меньше заданного) и числам степеней свободы k₁=n₁–1 и k₂=n₂–1 (k₁ – число степеней свободы большей исправленной дисперсии, k₂ – меньшей исправленной дисперсии) найти критическую точку .

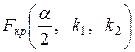3. Если F_набл<F_кр – нет оснований отвергнуть нулевую гипотезу.

Если F_набл>F_кр – нулевую гипотезу отвергают.