Метатеорема 2 и метатеорема 3.
Результаты двух последних теорем позволяют утверждать, что 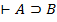 тогда и только тогда, когда
тогда и только тогда, когда 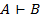 . Таким образом установлена связь м/у доказуемостью и выводимостью. Определим связь м/у доказуемостью и общезначимостью:
. Таким образом установлена связь м/у доказуемостью и выводимостью. Определим связь м/у доказуемостью и общезначимостью:
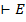 тогда и только тогда, когда
тогда и только тогда, когда 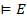 .
.
Введем определения:
Формульная аксиоматическая теория называется (просто) непротиворечивой, если ни для какой формулы А формулы А и 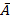 не являются обе доказуемыми в ней.
не являются обе доказуемыми в ней.
Формульная аксиоматическая теория называется (просто) противоречивой, если существует формула А, для которой одновременно А и 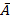 доказуемы в этой теории.
доказуемы в этой теории.
Теорема 4: Если 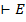 , то
, то 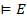 для любой формулы Е.
для любой формулы Е.
По условию Е доказуема, то есть заканчивается конечная последовательность формул, являющихся или аксиомами, или функциями, полученными по правилу MP из некоторых двух предшествующих формул. 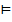 Аксиомы, согласно правилу MP формула В получается из формул А и
Аксиомы, согласно правилу MP формула В получается из формул А и 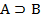 . Так как посылки А и
. Так как посылки А и 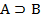 общезначимы, то
общезначимы, то 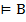 по определению импликации. Посылки обязательно будут
по определению импликации. Посылки обязательно будут 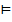 , т.к. у первой формулы формального доказательства выводимой по MP посылками являются аксиомы. Таким образом, все формулы формального доказательства общезначимы, общезначима и последовательность формул.
, т.к. у первой формулы формального доказательства выводимой по MP посылками являются аксиомы. Таким образом, все формулы формального доказательства общезначимы, общезначима и последовательность формул.
Следствие
Исчисление высказываний непротиворечива
Допустим, что исчисление высказываний противоречива. Тогда по определению противоречивой формальной аксиоматические теории доказана существуют формула А, такая, что 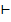 А и
А и 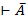 . Тогда по Т4
. Тогда по Т4 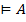 и
и 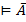 . По определению тавтологии формула А общезначима, если в любой интерпретации она принимает значение И. Поэтому вывод
. По определению тавтологии формула А общезначима, если в любой интерпретации она принимает значение И. Поэтому вывод 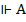 и
и 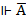 приводит к абсурду. Можно сделать вывод, что
приводит к абсурду. Можно сделать вывод, что 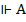 , если
, если 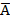 – противоречия.
– противоречия.
Рассмотрим теорему обращения МТ5, определяющую связь с логическим следованием и выводимостью.
Метатеорема 5:Для любого конечного множества формул Г и для любых формул А, В, С справедливы правила (введения и удаления), приведенные ниже:
| Введение | Удаление | |||||
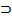 | Если Г, 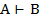 , то , то 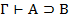 | ТД, ВИ | 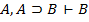 | МР, УИ | ||
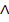 | 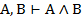 | ВК | 4,5 | 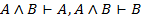 | УК1, УК2 | |
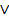 | 6,7 | 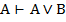 , , 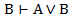 | ВД1, ВД2 | 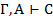 и и 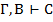 , то , то 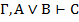 | УД | |
 | 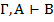 и и 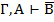 , то , то 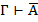 | RA,BO | 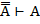 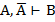 | УДО СУО | ||
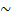 | 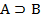 , , 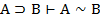 | ВЭ | 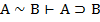 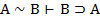 | УЭ1 УЭ2 |
Все правила доказываются с использованием АС и МР, из них уже доказаны 1 и 3. Правило 2 является исходящим правилом ИВ.
Докажем правило 8:
1. А
2. В
3. 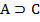
4. 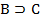
5. 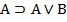
6. 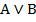
7. 
8. 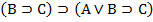
9. 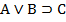
10. С
1. Посылка
2. Посылка
3. ВИ(1)
4. ВИ(2)
5. АС6
6. МР (F1,F2)
7. AC8
8. MP(F3,F7)
9. MP(F1,F8)
10. MP(F6,F9)
Подобным образом доказываются остальные правила.
Надо отметить, что здесь речь идет о правилах вывода, а не о правилах следования. Они имеют разные доказательства, но тем не менее предложение 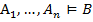 равносильно
равносильно 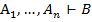 , различие лишь в описании одних и тех же правил.
, различие лишь в описании одних и тех же правил.
Доказанные правила описывают широко используемые рассуждения.
Чтобы доказать предложение линейной структуры 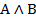 , обычно доказывают по отдельности А и В, а затем говорят «теорема доказана», т.е. доказуема
, обычно доказывают по отдельности А и В, а затем говорят «теорема доказана», т.е. доказуема 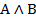 . То есть за фразой «теорема доказана» скрыт неявный переход от А и В к
. То есть за фразой «теорема доказана» скрыт неявный переход от А и В к 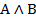 , т.е. правило ВК.
, т.е. правило ВК.
Например, при доказательстве предложения:
(1) «средняя линия трапеции параллельна основаниям и равна их полусумме» - 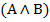
Доказывают каждое из предложений:
(2) «средняя линия трапеции параллельна основаниям» -(А)
(3) «средняя линия трапеции = n/сумме оснований» - (В)
и заканчивают доказательство словами «теорема доказана».
Правилам УК1,УК2 соответствуют предложения типа:
«Найдите среднюю линию трапеции с основанием А и С». Из предыдущих предложений – конечная (1) используют только его второй член В и находят среднюю линию трапеции 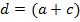 12/
12/
Предложения, имеющие пир-ру эквиваленции обычно выражают оборотами «т. А и т. Т, к. В» , « для того, чтобы А, необходимо и доказательство В», « если А, то В, и если В, то А» и некоторые уравнения.
Доказательство таких предложений распадается на две части:
1) Доказательство импликации 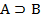
2) Доказательство импликации 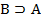
После этого заключается, что предложение доказано, т.е. 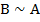 .
.
Полнота теории L.
В математике существует три важнейших математических проблемы:
Непротиворечивость,
полнота,
Разрешение.
Мы рассмотрим определение непротиворечивости. Введем понятие полноты.
Определение 1.19
Логической непротиворечивости исчислению называется полным относительно общезначимости, если в нем доказуема любая общезначимость формул.
Прежде чем установить полноту ИВ, необходимо доказать 4 лемма.
Лемма 1.1: Пусть д имеем логические операторы 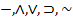 .
.
Для любой строки истинной таблицы любой из 5 операторов имеет место соответствия выводимость.
А 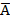 | Выводимость |
| 1. И Л 2. Л И | 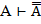 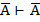 |
А В 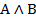 | Выводимость |
| 3. И И И 4. И Л Л 5. Л Л Л 6. Л Л Л | 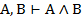 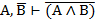 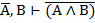 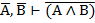 |
А В 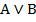 | |
| 7. И И И 8. И Л Л 9. Л И И 10. Л Л Л | 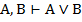 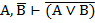 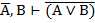 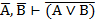 |
А В 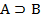 | Выводимость |
| 11. И И И 12. И Л Л 13. Л И И 14. Л Л И | 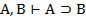 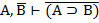 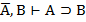 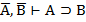 |
А В 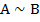 | |
| 15. И И И 16. И Л Л 17. Л И Л 18. Л Л И | 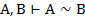 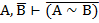 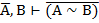 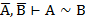 |
Установим некоторые из выводимостей.
(1) 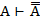
1. 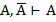 1.Т1а
1.Т1а
2. 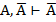 2.Т1а
2.Т1а
3. 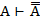 3.ВО(1,2)
3.ВО(1,2)
(9) 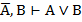
1. 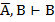 1.Т1а
1.Т1а
2. 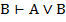 2.ВД2
2.ВД2
3. 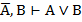 3.Т1б(1,2)
3.Т1б(1,2)
Распространим свойство леммы 1.1 на случай произвольной формулы.
Лемма 1.2: Для любой формулы существует, содержащий атомы  для любых из 2 строк ее истинной таблицы имеет место соответствия выводимость.
для любых из 2 строк ее истинной таблицы имеет место соответствия выводимость.
Доказательство данной леммы рассмотрим на л/з на конкретном примере.
Лемма 1.3: Если формула Е, содержащая атомы  (и только их), общезначима, то
(и только их), общезначима, то 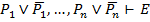 .
.
Ø Пусть n=2.
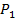
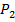 E
E
И И И
И Л И
Л И И
Л Л И
1. 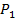 ,
, 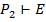
2. 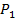 ,
, 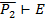
3. 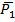 ,
, 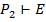
4. 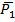 ,
, 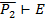
5. 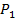 ,
, 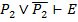 5.УД(F1,F2)
5.УД(F1,F2)
6. 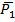 ,
, 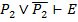 6.УД(F3,F1)
6.УД(F3,F1)
7. 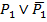 ,
, 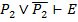 7.УД(F5,F6)
7.УД(F5,F6)
Доказательство в общем случае получается в результате применения правила УД 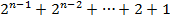 раз.
раз.
Лемма 1.4: 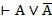 для любой формулы.
для любой формулы.
Метатеорема 6: Если 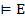 , то
, то 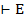 по лемме 1.4
по лемме 1.4  (1.6)
(1.6)
Так как формула Е общезначимо, то по лемме 1.3 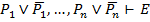 (1.7)
(1.7)
Из (1.6) и (1.7) по Т1б получим 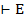 .
.
Следствие ИВ полна относительно общезначимости
Ø по определению полноты теория полна относительно общезначимости, если в ней доказуема любая общезначимая формула.
Согласно Т6 если формула общезначима, то формула доказуема.
