Алфавит, формулы, система аксиом схем и правило вывода исчисления высказываний.
ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
Алфавит, формулы, система аксиом схем и правило вывода исчисления высказываний.
В части 1.1 Мы рассмотрим алгебру высказываний. В алгебре высказывания изложение логики высказываний является содержательным, использующим аналитическое понятие истинностного значения. В исчислении высказываний изложение логики высказываний. Является формальным, построение с помощью аксиоматического метода. Возможны различные построения исчисления высказываний. Мы рассмотрим одно из них, называя теорией L.
Алфавит и определение формулы – те же что и в алгебре высказываний. Но буквам алфавита не приписывается никакой смысл, - это просто символы, которые можно распознавать и различать.
В алгебре высказываний мы описали класс общезначимые формул, выражающих законы логики на основе понятия истинностного значения. Здесь же законы логики – множество доказуемых формул – они описываются по-другому. Некоторые формулы принимаются в качестве “аксиом”, а для получения новых формул вводится некоторое “правило вывода”. Позже рассмотрим, что обе формулировки логики высказываний – алгебра высказываний и теория L – дают эквивалентные результаты.
Определение 1.14
Аксиомами теории L называются веские формулы, которые порождают нижеследующие формульные схемы при любом выборе формул A,B,C:
1. 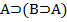
2. 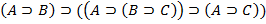
3. 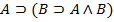
4. 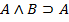
5. 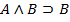
6. 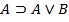
7. 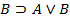
8. 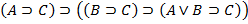
9. 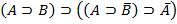
10. 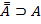
11. 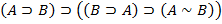
12. 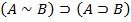
13. 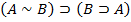
Каждая из схем (1)-(13) порождает счетное множество аксиом, если символы A, B, C заменять конкретными формулами. Поэтому записи (1)-(13) будем называть аксиомными схемами (AC).
Схемы (1)-(13) совпадают с первыми тринадцать формульными схемами предложения 1.6.
Определение 1.15
Правила вывода теории L называют процедуру перехода от двух формул вида A и 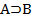 к одной формуле вида B для любых A и B. Это правило называется modus pondus, MP. Правило MP называют также правилом удаления импликант и обозначают УИ. Формулы A и
к одной формуле вида B для любых A и B. Это правило называется modus pondus, MP. Правило MP называют также правилом удаления импликант и обозначают УИ. Формулы A и 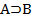 называют посылками, а B – заключением правила MP.
называют посылками, а B – заключением правила MP.
Формальное доказательство и формальный вывод.
Определение 1.16
Формальным доказательством (в теории L) называется конечная последовательность формул  , причем каждая формула этой последовательности либо аксиома, либо получена по правилу MP из каких-либо двух предшествующих формул этой последовательности. Формальное доказательство является доказательством своей последней формулы
, причем каждая формула этой последовательности либо аксиома, либо получена по правилу MP из каких-либо двух предшествующих формул этой последовательности. Формальное доказательство является доказательством своей последней формулы  . Формула B называется формально доказуемой, или формальной (теории L), если она имеет формальное доказательство.
. Формула B называется формально доказуемой, или формальной (теории L), если она имеет формальное доказательство.
Утверждение “Формула B формально доказуема в теории L” обозначается 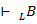 .
.
Введем соглашения:
a) Индекс L опускать;
b) Говорить «формальное доказательство», «формально доказуема», «формальная теорема» - доказательство «доказуема», «теорема».
Пример 1
Установить, что 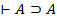
1. 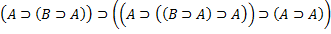 1. AC2 C=A,
1. AC2 C=A, 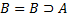
2. 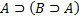 2. AC1
2. AC1
3. 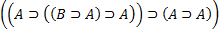 3. MP(2, 1)
3. MP(2, 1)
4. 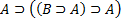 4. AC1
4. AC1 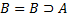
5. 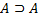 5.MP(4, 3)
5.MP(4, 3)
Пояснение AC2 A, 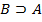 , B, C означает, что записано AC2, в которой формула С заменила формулой А, а формула В – формулой
, B, C означает, что записано AC2, в которой формула С заменила формулой А, а формула В – формулой 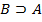 , пояснение MP(2, 1) означает, что формула получена в результате применения правила MP к формулам с номерами 2 и 1.
, пояснение MP(2, 1) означает, что формула получена в результате применения правила MP к формулам с номерами 2 и 1.
Следует заметить, что в проверенном доказательстве каждая из пяти формул. Является теоремой, в том числе и выписывание первые две аксиомы: доказательство любой аксиомы состоит из этой аксиомы.
Определение 1.17
Формальным выводом формулы B из формул, которые называются посылками или гипотезами 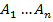 называется конечная последовательность формул
называется конечная последовательность формул 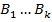 , заканчивающаяся формулой
, заканчивающаяся формулой 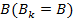 , причем каждая формула этой последовательности:
, причем каждая формула этой последовательности:
1. или одна из посылок 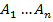 ;
;
2. или аксиома;
3. или формула, полученная из некоторых двух предшествующих формул этой последовательности по правилу MP.
Если 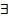 формальный вывод B из формул
формальный вывод B из формул 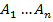 , то формула B называется формально выводимой из формул
, то формула B называется формально выводимой из формул 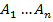 и обозначается:
и обозначается: 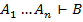 , или
, или 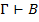 , где
, где 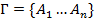 .
.
Очевидно, что доказательство – частный случай формального вывода из пустого множества посылок.
Введем соглашение: вместо «формальный вывод», «формально-выводима» будем говорить «вывод», «выводима».
В определениях 1.16 и 1.17 употребляемые термины «формальное доказательство», «формально доказуема», «формальный вывод», «формально-выводима» для явного указания на то, что эти доказательства и выводы строятся в предметной языки. Используемые слева от доказательства или вывода нумерация и справа от доказательства или вывода пояснения уже относится к метаязыку.
Пример 2
Установить, что 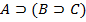 ,
, 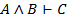 .
.
1. 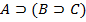 1. Посылка
1. Посылка
2. 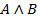 2. Посылка
2. Посылка
3. 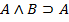 3. AC4
3. AC4
4. 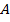 4.MP (2, 3)
4.MP (2, 3)
5. 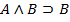 5. AC5
5. AC5
6. 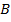 6. MP (2, 5)
6. MP (2, 5)
7. 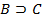 7. MP (4, 1)
7. MP (4, 1)
8. 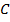 8. MP (6, 7)
8. MP (6, 7)
9. 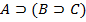 ,
, 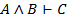 9. ОФВ- определение формального вывода (1-8)
9. ОФВ- определение формального вывода (1-8)
Запись 9 подытоживает формальный вывод формулы С из формул 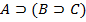 ,
, 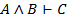 . Запись 9 сделана на метаязыке.
. Запись 9 сделана на метаязыке.
Метатеорема 1(МТ1).
a) 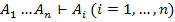 .
.
b) Если  и
и 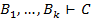 , то
, то 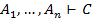
Доказательство
a) Для построения вывода формула 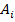 из формул
из формул 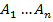 достаточно записать последовательно все формулы
достаточно записать последовательно все формулы 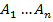 (в произвольном порядке), поместив последней формулу
(в произвольном порядке), поместив последней формулу 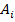 .
.
b) Заменив в данном выводе формулы С из формул  формулы
формулы  их данными выводами из формул
их данными выводами из формул 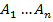 .
.
Метатеорема 2 (МТ2).
Пусть Г – любое множество формул.
Тогда:
a) Если Г 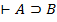 , то Г,
, то Г, 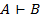 В частности
В частности
b) Если 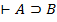 , то
, то 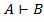
Следствие:
a) Если 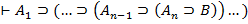 , то
, то 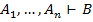 .
.
b) Если 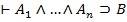 , то
, то 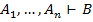 .
.
Метатеорема 3(МТ3).
Теорема дедукции (ТД), правило введения импликации (ВИ).
Пусть Г – любое множество формул.
Тогда:
c) Если Г, 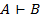 , то Г
, то Г 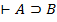 . В частности
. В частности
d) Если 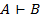 , то
, то 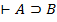 .
.
Доказательство
По условию МТ3 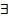 вывод
вывод 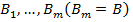 (1) формула B из множества формул
(1) формула B из множества формул 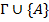 (данный вывод).
(данный вывод).
Требуется доказать существование вывода 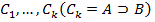 (2) формула
(2) формула 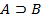 из формул множества Г (результирующий вывод).
из формул множества Г (результирующий вывод).
Опишем алгоритм превращения данного вывода (1) в результирующей вывод (2). К каждой формуле данного вывода (1) припишем слово « 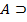 ». Тогда получим последовательность формул:
». Тогда получим последовательность формул:  , (3) заканчивающуюся нужной формулой
, (3) заканчивающуюся нужной формулой 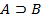 . Эта последовательность не является, вообще говоря, выводом из множества формул Г. Однако можно перед каждой формулой
. Эта последовательность не является, вообще говоря, выводом из множества формул Г. Однако можно перед каждой формулой 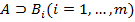 вставить дополнительные формулы так, чтобы превратить последовательность формул (3) в (2). Вывод дополнительных формул зависит от того, с каким обоснованием формула
вставить дополнительные формулы так, чтобы превратить последовательность формул (3) в (2). Вывод дополнительных формул зависит от того, с каким обоснованием формула 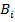 входит в данный вывод (1). Возможны 4 типа обоснований:
входит в данный вывод (1). Возможны 4 типа обоснований:
1. 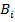 - посылка множества Г;
- посылка множества Г;
2. 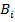 - посылка А;
- посылка А;
3. 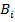 - аксиома;
- аксиома;
4. 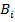 – формула, полученная по MP из двух предшествующих формул
– формула, полученная по MP из двух предшествующих формул 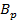 и
и 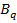 (p,q<i).
(p,q<i).
Рассмотрим каждый из этих случаев:
1. Пусть 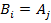 и
и 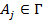 . В этом случае
. В этом случае 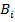 является посылкой не только в данном выводе (1), но и в результирующем выводе (2). Тогда перед формулой
является посылкой не только в данном выводе (1), но и в результирующем выводе (2). Тогда перед формулой 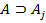 последовательности (3) вставим две формулы
последовательности (3) вставим две формулы 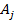 и
и 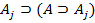 , из которых
, из которых 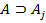 получается по правилу MP:
получается по правилу MP:
l. 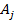 l. посылка
l. посылка
l+1. 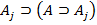 l+1. AC1
l+1. AC1 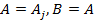
l+2. 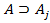 l+2. MP(l, l+1)
l+2. MP(l, l+1)
2. Пусть 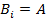 . Тогда
. Тогда 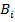 - посылка в данном выводе (1), но не является таковой в результирующем выводе (2). В последовательности (3) будет стоять формула
- посылка в данном выводе (1), но не является таковой в результирующем выводе (2). В последовательности (3) будет стоять формула 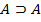 , которая является доказуемой (пример 1). Поэтому перед
, которая является доказуемой (пример 1). Поэтому перед 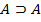 вставляем первые четыре формулы из ее доказательства.
вставляем первые четыре формулы из ее доказательства.
3. Пусть 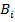 – аксиома. Тогда поступаем, как и в случае 1.
– аксиома. Тогда поступаем, как и в случае 1.
4. Пусть 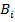 – формула, полученная по MP из формул
– формула, полученная по MP из формул 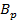 и
и 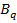 (p,q<i) последовательности (1). Тогда
(p,q<i) последовательности (1). Тогда 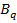 должна иметь вид
должна иметь вид 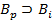 (или
(или 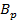 имеет вид
имеет вид 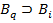 ). Итак,
). Итак, 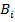 получена из
получена из 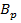 и
и 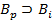 по MP. В последовательности (2) в этом случае будут формулы
по MP. В последовательности (2) в этом случае будут формулы 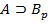 и
и 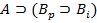 с некоторыми номерами S и t(S,t<i), и нужно обосновать включение в вывод (2) формула
с некоторыми номерами S и t(S,t<i), и нужно обосновать включение в вывод (2) формула 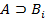 . Но формулы
. Но формулы 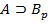 и
и 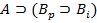 и
и 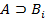 являются частями AC2. Таким образом, перед
являются частями AC2. Таким образом, перед 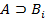 в данном случае необходимо вставить две формулы с номерами
в данном случае необходимо вставить две формулы с номерами 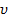 и
и 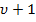 :
:
S. 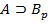 S
S
……… …
t. 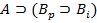 t
t
……… …
U. 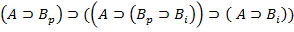 AC2
AC2 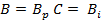
U+1. 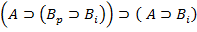 MP(S, U)
MP(S, U)
U+2. 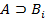 MP(t,
MP(t, 
Следствия:
a) Если 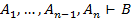 , то
, то 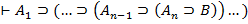 . В частности;
. В частности;
b) Если 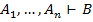 , то
, то 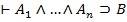 .
.
Определение 1.18
Формальная аксиоматическая теория называется (просто) непротиворечивой, если ни для какой формулы A и 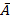 не являются обе доказуемыми в ней. Формальная аксиоматическая теория называется (просто) противоречивой, если существует формула A, для которой одновременно А и
не являются обе доказуемыми в ней. Формальная аксиоматическая теория называется (просто) противоречивой, если существует формула A, для которой одновременно А и 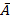 доказуемы в этой теории.
доказуемы в этой теории.
Метатеорема 4 (МТ4)
Если 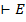 , то
, то 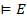 для любой формулы E.
для любой формулы E.
Следствие
Теория L непротиворечива.
Доказательство:
Допустим, что теория L противоречива. Тогда, согласно определению 1.18, существует формула А, такая, что 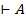 и
и 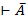 , и по МТ4
, и по МТ4 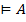 и
и 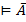 , что противоречит предложению 1.5.
, что противоречит предложению 1.5.
Полнота теории L.
В математике существует три важнейших математических проблемы:
Непротиворечивость,
полнота,
Разрешение.
Мы рассмотрим определение непротиворечивости. Введем понятие полноты.
Определение 1.19
Логической непротиворечивости исчислению называется полным относительно общезначимости, если в нем доказуема любая общезначимость формул.
Прежде чем установить полноту ИВ, необходимо доказать 4 лемма.
Лемма 1.1: Пусть д имеем логические операторы 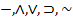 .
.
Для любой строки истинной таблицы любой из 5 операторов имеет место соответствия выводимость.
А 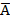 | Выводимость |
| 1. И Л 2. Л И | 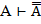 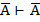 |
А В 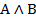 | Выводимость |
| 3. И И И 4. И Л Л 5. Л Л Л 6. Л Л Л | 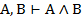 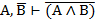 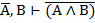 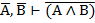 |
А В 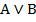 | |
| 7. И И И 8. И Л Л 9. Л И И 10. Л Л Л | 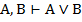 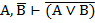 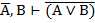 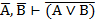 |
А В 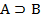 | Выводимость |
| 11. И И И 12. И Л Л 13. Л И И 14. Л Л И | 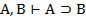 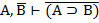 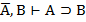 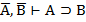 |
А В 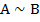 | |
| 15. И И И 16. И Л Л 17. Л И Л 18. Л Л И | 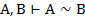 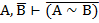 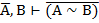 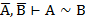 |
Установим некоторые из выводимостей.
(1) 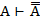
1. 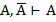 1.Т1а
1.Т1а
2. 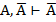 2.Т1а
2.Т1а
3. 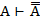 3.ВО(1,2)
3.ВО(1,2)
(9) 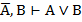
1. 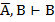 1.Т1а
1.Т1а
2. 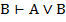 2.ВД2
2.ВД2
3. 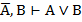 3.Т1б(1,2)
3.Т1б(1,2)
Распространим свойство леммы 1.1 на случай произвольной формулы.
Лемма 1.2: Для любой формулы существует, содержащий атомы  для любых из 2 строк ее истинной таблицы имеет место соответствия выводимость.
для любых из 2 строк ее истинной таблицы имеет место соответствия выводимость.
Доказательство данной леммы рассмотрим на л/з на конкретном примере.
Лемма 1.3: Если формула Е, содержащая атомы  (и только их), общезначима, то
(и только их), общезначима, то 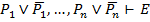 .
.
Ø Пусть n=2.
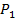
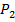 E
E
И И И
И Л И
Л И И
Л Л И
1. 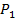 ,
, 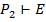
2. 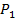 ,
, 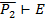
3. 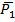 ,
, 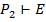
4. 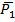 ,
, 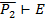
5. 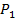 ,
, 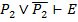 5.УД(F1,F2)
5.УД(F1,F2)
6. 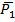 ,
, 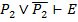 6.УД(F3,F1)
6.УД(F3,F1)
7. 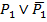 ,
, 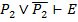 7.УД(F5,F6)
7.УД(F5,F6)
Доказательство в общем случае получается в результате применения правила УД 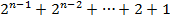 раз.
раз.
Лемма 1.4: 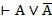 для любой формулы.
для любой формулы.
Метатеорема 6: Если 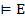 , то
, то 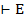 по лемме 1.4
по лемме 1.4  (1.6)
(1.6)
Так как формула Е общезначимо, то по лемме 1.3 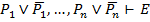 (1.7)
(1.7)
Из (1.6) и (1.7) по Т1б получим 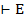 .
.
Следствие ИВ полна относительно общезначимости
Ø по определению полноты теория полна относительно общезначимости, если в ней доказуема любая общезначимая формула.
Согласно Т6 если формула общезначима, то формула доказуема.
ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
Алфавит, формулы, система аксиом схем и правило вывода исчисления высказываний.
В части 1.1 Мы рассмотрим алгебру высказываний. В алгебре высказывания изложение логики высказываний является содержательным, использующим аналитическое понятие истинностного значения. В исчислении высказываний изложение логики высказываний. Является формальным, построение с помощью аксиоматического метода. Возможны различные построения исчисления высказываний. Мы рассмотрим одно из них, называя теорией L.
Алфавит и определение формулы – те же что и в алгебре высказываний. Но буквам алфавита не приписывается никакой смысл, - это просто символы, которые можно распознавать и различать.
В алгебре высказываний мы описали класс общезначимые формул, выражающих законы логики на основе понятия истинностного значения. Здесь же законы логики – множество доказуемых формул – они описываются по-другому. Некоторые формулы принимаются в качестве “аксиом”, а для получения новых формул вводится некоторое “правило вывода”. Позже рассмотрим, что обе формулировки логики высказываний – алгебра высказываний и теория L – дают эквивалентные результаты.
Определение 1.14
Аксиомами теории L называются веские формулы, которые порождают нижеследующие формульные схемы при любом выборе формул A,B,C:
1. 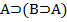
2. 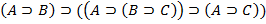
3. 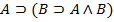
4. 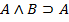
5. 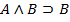
6. 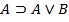
7. 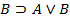
8. 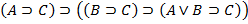
9. 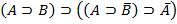
10. 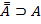
11. 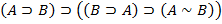
12. 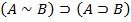
13. 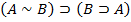
Каждая из схем (1)-(13) порождает счетное множество аксиом, если символы A, B, C заменять конкретными формулами. Поэтому записи (1)-(13) будем называть аксиомными схемами (AC).
Схемы (1)-(13) совпадают с первыми тринадцать формульными схемами предложения 1.6.
Определение 1.15
Правила вывода теории L называют процедуру перехода от двух формул вида A и 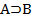 к одной формуле вида B для любых A и B. Это правило называется modus pondus, MP. Правило MP называют также правилом удаления импликант и обозначают УИ. Формулы A и
к одной формуле вида B для любых A и B. Это правило называется modus pondus, MP. Правило MP называют также правилом удаления импликант и обозначают УИ. Формулы A и 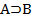 называют посылками, а B – заключением правила MP.
называют посылками, а B – заключением правила MP.
