Инструкция по работе с тетрадью

Рабочая тетрадь предназначена для организации аудиторной и самостоятельной работы студентов, выбравших профессию учителя начальных классов. Будущий учитель должен не только уметь решать те задачи, которые он будет предлагать для решения на уроках младшим школьникам, но и понимать, какие теоретические положения лежат в основе начального курса математики.

При составлении рабочей тетради использовался материал учебника Л.П. Стойловой «Математика», предназначенного для обучения будущих учителей начальных классов, а также составляющего комплект с данным учебником сборника задач авторов Л.П. Стойловой, Е.А. Конобеевой, И.В. Шадриной. Кроме того, в тетрадь включены задания из учебников математики для начальной школы по программам «Школа России», «Перспектива» и сборников текстовых задач Т.Н. Максимовой, О.А. Мокрушиной.

Все задания студенты выполняют непосредственно в тетради. В каждом задании предусмотрено место для вписывания решения и/или ответа. В зависимости от задания студентам предлагается выбрать и вписать в соответствующие строки правильные ответы, нарисовать рисунок, заполнить таблицу, написать полное решение с пояснением или письменно ответить на вопрос.

Тема 1. Множества и операции над ними

Теоретический материал

Те или иные группы объектов, рассматриваемые как единое целое: геометрические фигуры, действительные числа, четные числа и т.д. – называют множествами.

Обозначения:

Множества: прописные буквы латинского алфавита (A, B, C, …, Z).

Пустое множество: .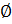

Элементы множества: строчные буквы латинского алфавита ( ).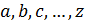

Объект 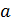принадлежит множеству : .

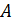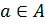Объект 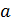не принадлежит множеству : .

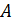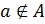Числовые множества:

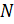– множество натуральных чисел;

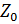– множество целых неотрицательных чисел ( 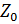= 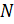+ нуль);

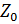– множество целых чисел ( = + целые отрицательные числа);

– множество рациональных чисел ( = + дробные числа);

– множество действительных чисел ( = + иррациональные числа).

Способы задания множеств:

1. Перечислением всех его элементов.

2. Указанием характеристического свойства.

Отношения между множествами и их изображение с помощью кругов Эйлера:

1. Непересекающиеся множества

A

B

2. Пересекающиеся множества

A

B

3. Множество B является подмножеством A ( .

B

A

4. Множество A=B

A=B

Пересечение множеств ( )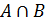

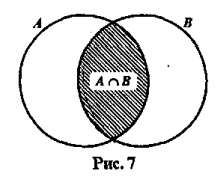
Объединение множеств ( ):

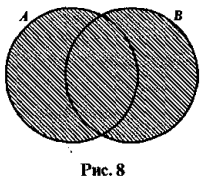
Разность множеств (A \ B)

Подмножество ( )

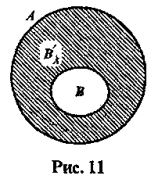
Задания

1. Какие множества из перечисленных являются бесконечными, конечными, пустыми?

а) множество целых неотрицательных чисел;

б) множество букв латинского алфавита;

в) множество натуральных однозначных чисел;

г) множество точек пересечения параллельных прямых;

д) множество точек на прямой;

е) множество точек пересечения перпендикулярных прямых;

ж) множество дней в году;

з) множество вершин прямоугольника.

Конечные: ____________________________________________________

_____________________________________________________________

Бесконечные: _________________________________________________

_____________________________________________________________

Пустые: ______________________________________________________

_____________________________________________________________

2. Запишите с помощью символов:

а) множество C не является подмножеством множества D;

б) множество A является подмножеством множества B;

в) множества G и H равны;

г) множества M и N не равны.

3. Множества заданы посредством указания его характеристического свойства. Можно ли задать эти множества посредством перечисления элементов? Если возможно, сделайте это.

а) множество простых однозначных чисел;

б) множество четных чисел, меньших или равных 20;

в) множество двузначных чисел, кратных 15.

4. Укажите характеристическое свойство множества:

а) ;

б) ;

в) .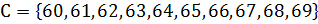

5. Запишите в символической форме множества A и B, если:

а) А – множество натуральных чисел, больших 5;

б) B – множество натуральных чисел, больших 3 и не больших 5.

6. Изобразить на координатной прямой множество решений неравенства, если :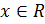

а) ;

б) ;

в) ;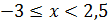

г) .

7. Множества A и B заданы посредством перечисления элементов. Найдите пересечение множеств.

а) ;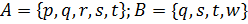

б) ;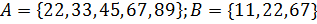

в) .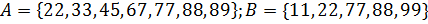

8. Множества A и B заданы посредством указания характеристического свойства. В каком случае множества A и B пересекаются?

а) 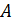– множество нечетных однозначных чисел, B – множество четных однозначных чисел;

б) 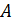– множество равнобедренных треугольников, B – множество прямоугольных треугольников;

в) 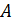– множество чисел, кратных 4, B – множество двузначных чисел, меньших 50.

9. Изобразите с помощью кругов Эйлера следующие множества:

I. Множества:

1. Города.

2. Столицы.

II. Множества:

1. Каменные дома.

2. Трехэтажные дома.

III. Множества:

1. Числа, кратные 3.

2. Числа, кратные 5.

IV. Множества:

1. Птицы.

2. Животные.

V. Множества:

1. Студенты.

2. Спортсмены.

VI. Множества:

1. .

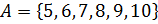2. .

VII. Множества:

1. Деревья.

2. Хвойные деревья.

VIII. Множества:

1. Журналы.

2. Печатные издания.

IX. Множества:

1. Четные двузначные числа.

2. Четные числа, меньшие 150.

X. Множества:

1. .

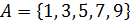2. .

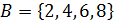XI. Множества:

1. Прямоугольные треугольники.

2. Равнобедренные треугольники.

XII. Множества:

1. A – множество двузначных чисел.

2. .

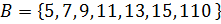XIII. Множества:

1. Полосатые животные.

2. Хищные животные.

XIV. Множества:

1. .

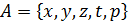2. .

10. Какие стандартные обозначения используются для следующих числовых множеств:

а) множество натуральных чисел _______;

б) множество целых неотрицательных чисел______;

в) множество целых чисел______;

г) множество рациональных чисел________;

д) множество действительных чисел________?

Нарисуйте круги Эйлера для этих множеств.

11. Установите, какие из чисел: -2,5; 6; -12; 0; 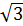являются:

а) натуральными___________________________________________;

б) целыми неотрицательными________________________________;

в) целыми_________________________________________________;

г) рациональными__________________________________________;

д) действительными________________________________________.

Запишите некоторые утверждения с помощью символов.

12. Задано множество 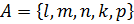. Множество B не является подмножеством множества A. Каким может быть множество B? Рассмотрите различные случаи и изобразите множества A и B с помощью кругов Эйлера.

13. Установите, в каких отношениях находятся множества A и B и изобразите эти множества с помощью кругов Эйлера, если:

а) , ;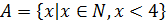

б) , ;

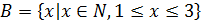в) , ;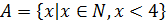

г) , .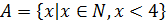

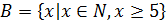14. Даны множества A, B и C. Изобразите отношения между множествами с помощью кругов Эйлера.

а) , ,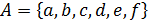

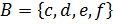б) , ,

в) , ,

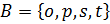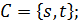
г) , , .

15. Даны множества: A – множество четных чисел; B – множество чисел, кратных 3; С – множество чисел, кратных 5. Дайте интерпретацию следующих множеств и изобразите их с помощью кругов Эйлера:

а) ;

б) ;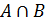

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и) ;

к) .

16. Какие понятия теории множеств используются при решении данной задачи (Дорофеев, Г.В., Миракова, Т.Н. Математика. 1 класс: учебник. В 2 ч. Ч.1, с. 51)?

_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

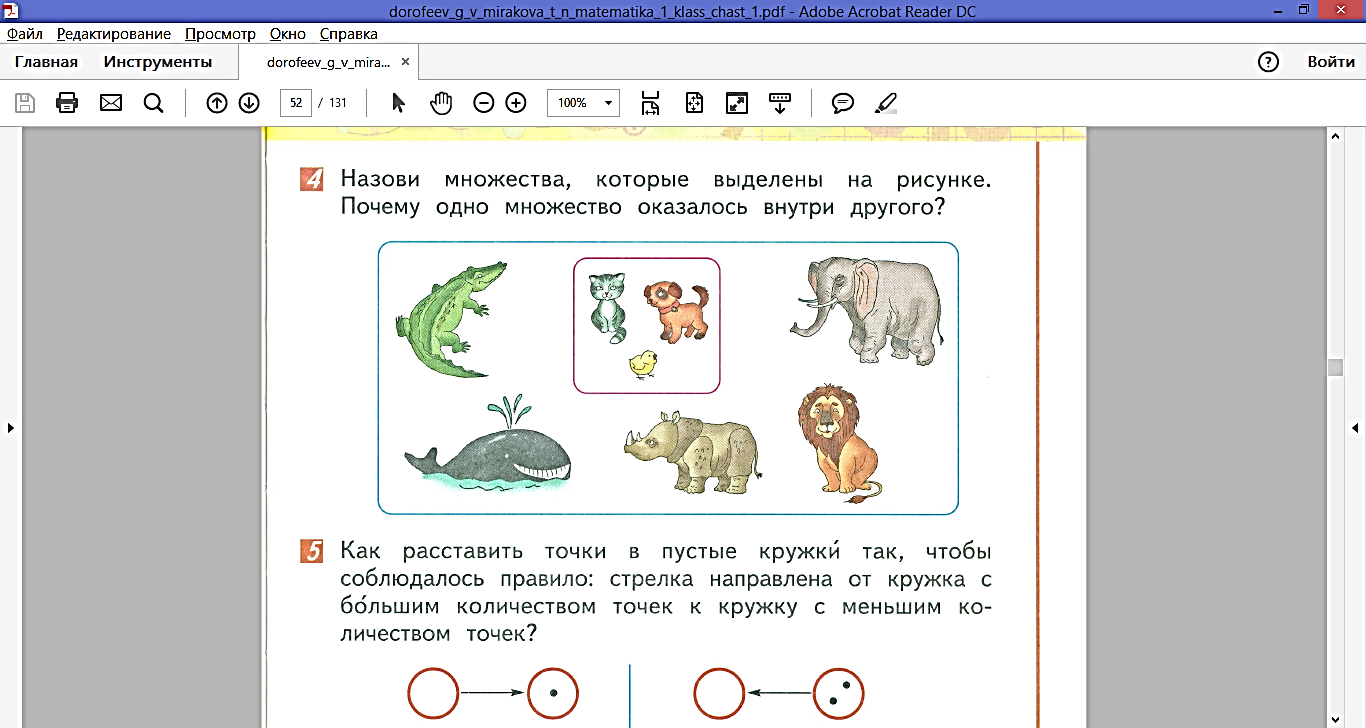
17. Придумайте две задачи для младших школьников с использованием понятий теории множеств.

Задача № 1

Задача № 2