Рабочая тетрадь по математике
Ю.В. Корчемкина
Рабочая тетрадь по математике
Министерство образования и науки российской федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Южно-Уральский государственный гуманитарно-педагогический университет»
Ю.В. Корчемкина
Рабочая тетрадь по математике
Челябинск
УДК 51(021)
ББК 22.1я73
К 70
Корчемкина, Ю.В. Рабочая тетрадь по математике [Текст] / Ю.В. Корчемкина. – Челябинск: Изд-во ЮУрГГПУ, 2017. – 88 с.
ISBN
Рабочая тетрадь предназначена для студентов образовательных организаций высшего образования, обучающихся по направлению подготовки Педагогическое образование, профиль Начальное образование, а также Педагогическое образование (с двумя профилями подготовки) с первым профилем Начальное образование. Рабочая тетрадь также может быть использована при работе со студентами колледжей, получающих образование по специальностям Преподавание в начальных классах, Дошкольное образование, Специальное дошкольное образование и др.
В рабочую тетрадь включены такие разделы курса математики, как «Множества», «Запись целых неотрицательных чисел и алгоритмы действий над ними», «Текстовые задачи». В тетради содержится краткий теоретический материал и практические задания по соответствующим разделам. Задания направлены на формирование профессиональных компетенций будущих учителей начальных классов.
Рецензенты:
Махмутова Л.Г., канд. пед. наук, доцент
Овсяницкая Л.Ю., канд. техн. наук, доцент
ISBN
© Ю.В. Корчемкина, 2017
© Издательство Южно-Уральского государственного
гуманитарно-педагогического университета, 2017
Содержание
Инструкция по работе с тетрадью.. 4
Тема 1. Множества и операции над ними. 5
Тема 2. Разбиение объектов на классы.. 21
Тема 3. Число элементов в объединении и разности конечных множеств. 32
Тема 4. Декартово произведение множеств. 37
Тема 5. Математические понятия. 42
Тема 6. Запись целых неотрицательных чисел и алгоритмы действий над ними 48
Тема 7. Текстовая задача и процесс ее решения. 65
Приложения. 83
Приложение 1. Алгоритмы письменных вычислений в десятичной системе счисления 83
Приложение 2. Методы решения текстовых задач. 87
Библиографический список. 88
Инструкция по работе с тетрадью
Рабочая тетрадь предназначена для организации аудиторной и самостоятельной работы студентов, выбравших профессию учителя начальных классов. Будущий учитель должен не только уметь решать те задачи, которые он будет предлагать для решения на уроках младшим школьникам, но и понимать, какие теоретические положения лежат в основе начального курса математики.
При составлении рабочей тетради использовался материал учебника Л.П. Стойловой «Математика», предназначенного для обучения будущих учителей начальных классов, а также составляющего комплект с данным учебником сборника задач авторов Л.П. Стойловой, Е.А. Конобеевой, И.В. Шадриной. Кроме того, в тетрадь включены задания из учебников математики для начальной школы по программам «Школа России», «Перспектива» и сборников текстовых задач Т.Н. Максимовой, О.А. Мокрушиной.
Все задания студенты выполняют непосредственно в тетради. В каждом задании предусмотрено место для вписывания решения и/или ответа. В зависимости от задания студентам предлагается выбрать и вписать в соответствующие строки правильные ответы, нарисовать рисунок, заполнить таблицу, написать полное решение с пояснением или письменно ответить на вопрос.
Тема 1. Множества и операции над ними
Теоретический материал
Те или иные группы объектов, рассматриваемые как единое целое: геометрические фигуры, действительные числа, четные числа и т.д. – называют множествами.
Обозначения:
Множества: прописные буквы латинского алфавита (A, B, C, …, Z).
Пустое множество: 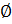 .
.
Элементы множества: строчные буквы латинского алфавита ( 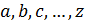 ).
).
Объект 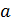 принадлежит множеству
принадлежит множеству 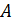 :
: 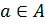 .
.
Объект 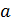 не принадлежит множеству
не принадлежит множеству 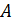 :
: 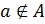 .
.
Числовые множества:
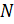 – множество натуральных чисел;
– множество натуральных чисел;
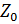 – множество целых неотрицательных чисел (
– множество целых неотрицательных чисел ( 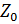 =
= 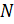 + нуль);
+ нуль);
 – множество целых чисел (
– множество целых чисел (  =
= 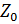 + целые отрицательные числа);
+ целые отрицательные числа);
 – множество рациональных чисел (
– множество рациональных чисел (  =
=  + дробные числа);
+ дробные числа);
 – множество действительных чисел (
– множество действительных чисел (  =
=  + иррациональные числа).
+ иррациональные числа).
Способы задания множеств:
1. Перечислением всех его элементов.
2. Указанием характеристического свойства.
Отношения между множествами и их изображение с помощью кругов Эйлера:
1. Непересекающиеся множества
| A |
| B |
2. Пересекающиеся множества
| A |
| B |
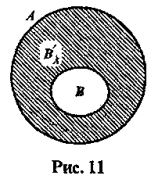
3. Множество B является подмножеством A (  .
.
| B |
| A |
4. Множество A=B
| A=B |
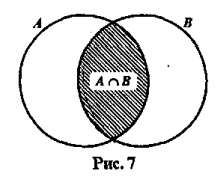
Пересечение множеств ( 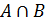 )
)
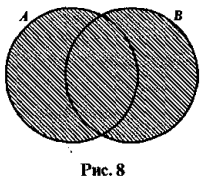
Объединение множеств (  ):
):
Разность множеств (A \ B)

Подмножество (  )
)
Задания
1. Какие множества из перечисленных являются бесконечными, конечными, пустыми?
а) множество целых неотрицательных чисел;
б) множество букв латинского алфавита;
в) множество натуральных однозначных чисел;
г) множество точек пересечения параллельных прямых;
д) множество точек на прямой;
е) множество точек пересечения перпендикулярных прямых;
ж) множество дней в году;
з) множество вершин прямоугольника.
Конечные: ____________________________________________________
_____________________________________________________________
Бесконечные: _________________________________________________
_____________________________________________________________
Пустые: ______________________________________________________
_____________________________________________________________
2. Запишите с помощью символов:
а) множество C не является подмножеством множества D;
б) множество A является подмножеством множества B;
в) множества G и H равны;
г) множества M и N не равны.
3. Множества заданы посредством указания его характеристического свойства. Можно ли задать эти множества посредством перечисления элементов? Если возможно, сделайте это.
а) множество простых однозначных чисел;
б) множество четных чисел, меньших или равных 20;
в) множество двузначных чисел, кратных 15.
4. Укажите характеристическое свойство множества:
а)  ;
;
б)  ;
;
в) 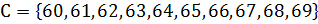 .
.
5. Запишите в символической форме множества A и B, если:
а) А – множество натуральных чисел, больших 5;
б) B – множество натуральных чисел, больших 3 и не больших 5.
6. Изобразить на координатной прямой множество решений неравенства, если 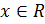 :
:
а)  ;
;
б)  ;
;
в) 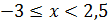 ;
;
г)  .
.
7. Множества A и B заданы посредством перечисления элементов. Найдите пересечение множеств.
а) 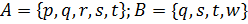 ;
;
б) 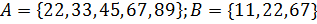 ;
;
в) 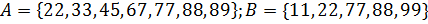 .
.
8. Множества A и B заданы посредством указания характеристического свойства. В каком случае множества A и B пересекаются?
а)  – множество нечетных однозначных чисел, B – множество четных однозначных чисел;
– множество нечетных однозначных чисел, B – множество четных однозначных чисел;
б) 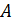 – множество равнобедренных треугольников, B – множество прямоугольных треугольников;
– множество равнобедренных треугольников, B – множество прямоугольных треугольников;
в) 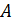 – множество чисел, кратных 4, B – множество двузначных чисел, меньших 50.
– множество чисел, кратных 4, B – множество двузначных чисел, меньших 50.
9. Изобразите с помощью кругов Эйлера следующие множества:
I. Множества:
1. Города.
2. Столицы.
II. Множества:
1. Каменные дома.
2. Трехэтажные дома.
III. Множества:
1. Числа, кратные 3.
2. Числа, кратные 5.
IV. Множества:
1. Птицы.
2. Животные.
V. Множества:
1. Студенты.
2. Спортсмены.
VI. Множества:
1. 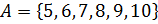 .
.
2.  .
.
VII. Множества:
1. Деревья.
2. Хвойные деревья.
VIII. Множества:
1. Журналы.
2. Печатные издания.
IX. Множества:
1. Четные двузначные числа.
2. Четные числа, меньшие 150.
X. Множества:
1. 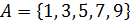 .
.
2. 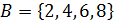 .
.
XI. Множества:
1. Прямоугольные треугольники.
2. Равнобедренные треугольники.
XII. Множества:
1. A – множество двузначных чисел.
2. 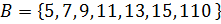 .
.
XIII. Множества:
1. Полосатые животные.
2. Хищные животные.
XIV. Множества:
1. 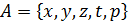 .
.
2.  .
.
10. Какие стандартные обозначения используются для следующих числовых множеств:
а) множество натуральных чисел _______;
б) множество целых неотрицательных чисел______;
в) множество целых чисел______;
г) множество рациональных чисел________;
д) множество действительных чисел________?
Нарисуйте круги Эйлера для этих множеств.
11. Установите, какие из чисел: -2,5; 6; -12; 0; 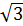 являются:
являются:
а) натуральными___________________________________________;
б) целыми неотрицательными________________________________;
в) целыми_________________________________________________;
г) рациональными__________________________________________;
д) действительными________________________________________.
Запишите некоторые утверждения с помощью символов.
12. Задано множество 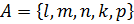 . Множество B не является подмножеством множества A. Каким может быть множество B? Рассмотрите различные случаи и изобразите множества A и B с помощью кругов Эйлера.
. Множество B не является подмножеством множества A. Каким может быть множество B? Рассмотрите различные случаи и изобразите множества A и B с помощью кругов Эйлера.
13. Установите, в каких отношениях находятся множества A и B и изобразите эти множества с помощью кругов Эйлера, если:
а) 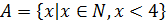 ,
,  ;
;
б)  ,
, 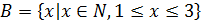 ;
;
в) 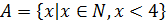 ,
,  ;
;
г) 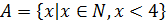 ,
, 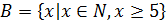 .
.
14. Даны множества A, B и C. Изобразите отношения между множествами с помощью кругов Эйлера.
а) 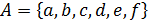 ,
, 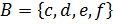 ,
, 
б)  ,
,  ,
, 
в)  ,
, 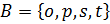 ,
, 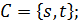
г)  ,
,  ,
,  .
.
15. Даны множества: A – множество четных чисел; B – множество чисел, кратных 3; С – множество чисел, кратных 5. Дайте интерпретацию следующих множеств и изобразите их с помощью кругов Эйлера:
а)  ;
;
б) 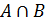 ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  ;
;
ж)  ;
;
з)  ;
;
и)  ;
;
к)  .
.
16. Какие понятия теории множеств используются при решении данной задачи (Дорофеев, Г.В., Миракова, Т.Н. Математика. 1 класс: учебник. В 2 ч. Ч.1, с. 51)?
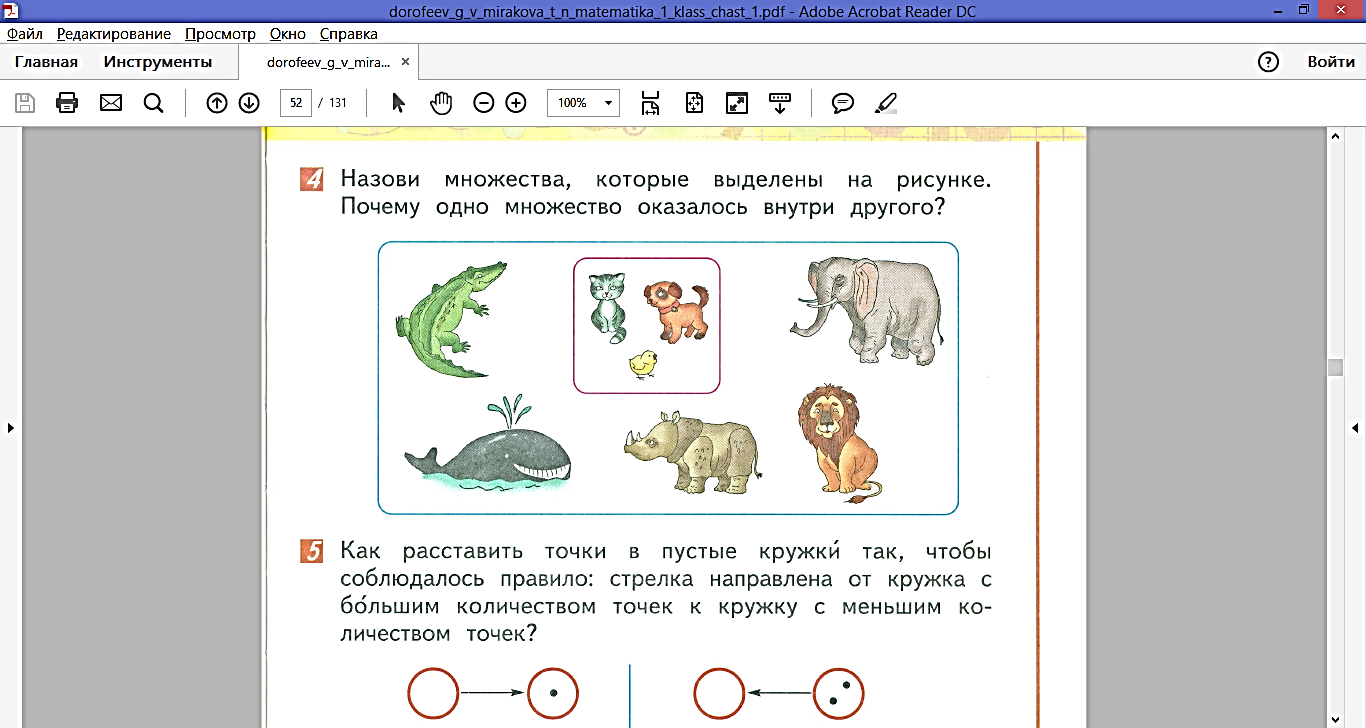
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
17. Придумайте две задачи для младших школьников с использованием понятий теории множеств.
Задача № 1
Задача № 2
Теоретический материал
Классификация – распределение объектов по классам.
Считают, что множество X разбито на классы 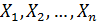 , если:
, если:
- подмножества 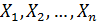 попарно не пересекаются;
попарно не пересекаются;
- объединение подмножеств 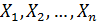 совпадает с множеством X.
совпадает с множеством X.
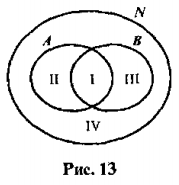
Задания
1. Из множества 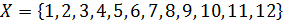 выделили подмножества
выделили подмножества  ,
, 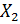 ,
,  . В каких из следующих случаев множество
. В каких из следующих случаев множество  оказалось разбитым на классы [7, c.31]:
оказалось разбитым на классы [7, c.31]:
а)  ,
, 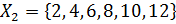 ,
, 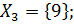
б)  ,
, 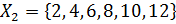 ,
, 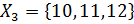 ;
;
в) 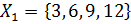 ,
,  ,
, 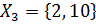 ?
?
Верная классификация: _______________________.
Неверная классификация:______________________.
2. На множестве четырехугольников рассматриваются два свойства.
На какие классы разобьется множество этих свойств? Начертите по два четырехугольника каждого класса.
а) «быть прямоугольником» и «быть квадратом»;
Классы:______________________________________________________
_____________________________________________________________
б) «быть прямоугольником» и «быть ромбом»;
Классы:______________________________________________________
_____________________________________________________________
в) «быть прямоугольником» и «быть трапецией».
Классы:______________________________________________________
_____________________________________________________________
3. Числа 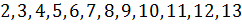 расклассифицированы тремя способами. Укажите основание каждой классификации.
расклассифицированы тремя способами. Укажите основание каждой классификации.
a) 2 10 б) 2 4 в) 3 2
3 11 3 6 6 4
4 12 5 8 9 5
5 13 7 10 12 7
6 9 12 8
7 11 10
8 13 11
9 13
Основание:
а) ___________________________________________________________
б) ___________________________________________________________
в) ___________________________________________________________
4. В учебнике математики для первого класса (Дорофеев, Г.В., Миракова, Т.Н. Математика. 1 класс: учебник. В 2 ч. Ч.1, с. 35) ученикам предлагается разбить на части следующее множество фигур по различным основаниям (выполнить дихотомическую классификацию). Какие основания для классификации можно выделить?
Основания:
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
5. Изобразите с помощью кругов Эйлера следующие множества, проведите классификацию, охарактеризуйте каждый полученный класс:
а) множества:
1. Игрушки.
2. Заводные игрушки.
3. Куклы.
4. Заводные автомобили.
5. Пистолеты.
6. Куклы Barbie.
Обозначения:
________________________
________________________
________________________
________________________
________________________
________________________
Классы:
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
б) множества:
1. Автобусы.
2. Трамваи.
3. Троллейбусы.
4. Общественный транспорт.
5. Транспортные средства.
6. Грузовые автомобили.
Обозначения:
________________________
________________________
________________________
________________________
________________________
________________________
Классы:
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
в) множества:
1. Вузы.
2. Университеты.
3. Колледжи.
4. Школы.
5. Учебные заведения.
Обозначения:
________________________
________________________
________________________
________________________
________________________
________________________
Классы:
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
г) множества:
1. Печатные СМИ.
2. Телевидение.
3. Средства массовой информации.
4. Газеты.
5. Журналы.
Обозначения:
________________________
________________________
________________________
________________________
________________________
________________________
Классы:
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
д) множества:
1. Диваны.
2. Кровати.
3. Мебель.
4. Диваны-кровати.
5. Стулья.
6. Столы.
7. Компьютерные стулья.
Обозначения:
________________________
________________________
________________________
________________________
________________________
________________________
Классы:
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
е) множества:
1. Математика.
2. Физика.
3. Гуманитарные предметы.
4. Литература.
5. История.
6. Школьные предметы.
Обозначения:
________________________
________________________
________________________
________________________
________________________
________________________
Классы:
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
6. Является ли данная задача (Дорофеев, Г.В., Миракова, Т.Н. Математика. 1 класс: учебник. В 2 ч. Ч.1, с. 45) задачей на классификацию? Каким термином в начальной школе называют классы? Решите данную задачу.
Множество___________________________________________________
Классы_______________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
7. Является ли данная задача (Дорофеев, Г.В., Миракова, Т.Н. Математика. 1 класс: учебник. В 2 ч. Ч.1, с. 57) задачей на классификацию? Ответьте на вопросы задачи.
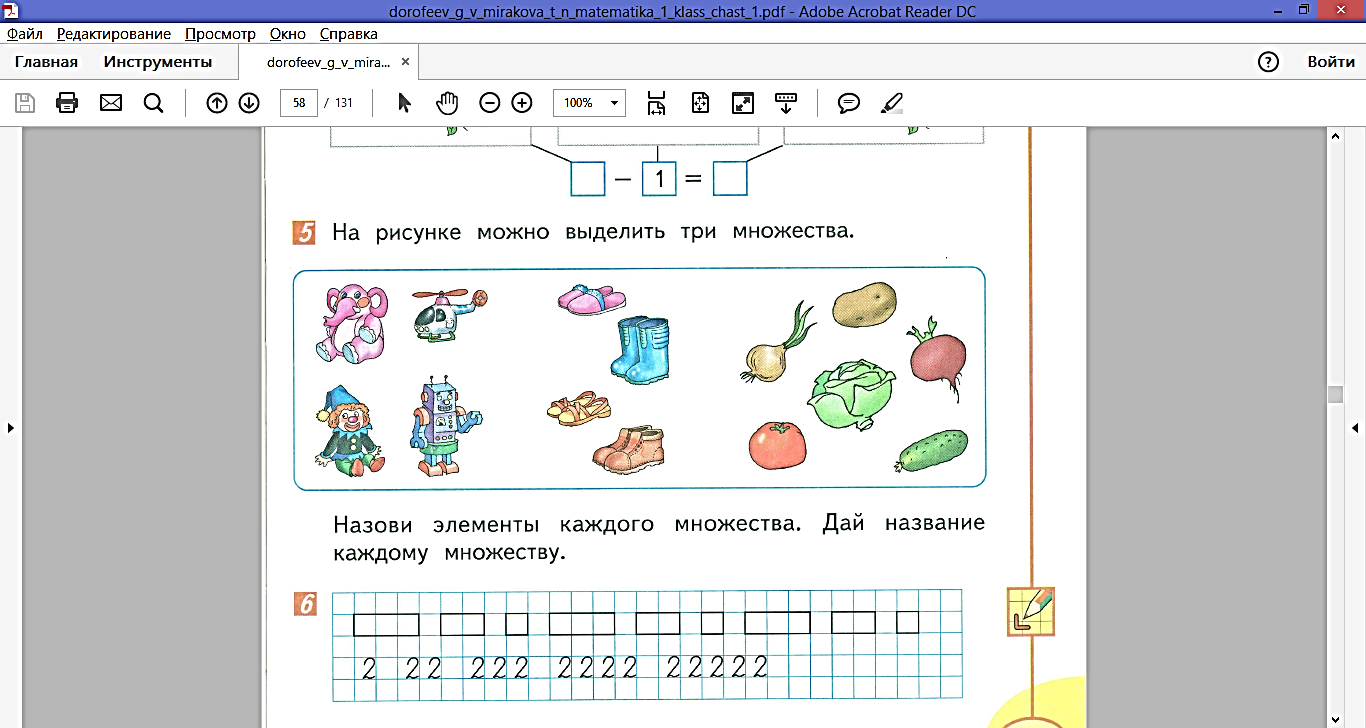
____________________________________________________________
____________________________________________________________
____________________________________________________________
____________________________________________________________
____________________________________________________________
____________________________________________________________
____________________________________________________________
____________________________________________________________
8. Придумайте три задачи для младших школьников, используя понятие классификации множеств.
Задача № 1
Задача № 2
Задача № 3
Теоретический материал
Обозначения:
 – количество элементов в множестве A;
– количество элементов в множестве A;
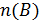 – количество элементов в множестве B;
– количество элементов в множестве B;
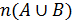 – количество элементов в объединении множеств A и B;
– количество элементов в объединении множеств A и B;
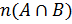 – количество элементов в пересечении множеств A и B.
– количество элементов в пересечении множеств A и B.
Если 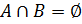 , то
, то 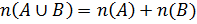 .
.
Если  , то
, то 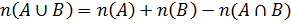 .
.
Если 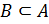 , то
, то 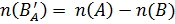 .
.
Задания
1. Изобразите с помощью кругов Эйлера множества, о которых идет речь в задачах:
а) из 30 учеников 15 увлекается биологией, а 12 – математикой;
б) в классе 25 учащихся, из них 18 играют в баскетбол, а 15 – в волейбол.
2. В первых классах все участвуют в самодеятельности: 52 ученика поют в хоре, 37 учеников занимаются в танцевальном кружке, а 4 ученика и поют, и танцуют. Сколько учащихся в первых классах?
3. Из 32 учеников класса 12 занимаются в математическом кружке, 15 – в биологическом, 8 человек занимаются и в том, и в другом кружке. Сколько учеников не занимаются ни в одном из кружков?
4. Света положила в коробку 6 треугольников, 3 красных многоугольника и 4 синих круга. Сколько в коробке красных треугольников, если всего в ней оказалось 11 фигурок?
5. Из 100 человек английский язык изучают 28, немецкий – 30, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 5. Остальные изучают только испанский. Все три языка изучают три студента. Сколько студентов изучает более одного языка? Сколько студентов изучает испанский язык?
6. На уроке литературы учитель провел опрос, какие книги читали его ученики. Из 40 опрошенных сборник фантастики (F) читали 25 учеников, книгу современного прозаика (S) – 22 ученика, книгу поэта-классика (P) – также 22. Книгу F или S читали 33 школьника, F или P – 32, P или S – 31. Только 10 учащихся прочли все 3 книги. Сколько учеников не читали ни одной из этих трех книг? Сколько учеников прочли только по одной книге?
7. В классе 30 учеников, из них 15 учеников посещает химический кружок, 11 – биологический, 4 ученика – и химический, и биологический. 5 учеников участвуют в работе математического и химического кружка, а 3 – математического и биологического. Все три кружка посещает 1 ученик. Остальные учащиеся занимаются только в математическом кружке. Сколько всего учеников занимаются в математическом кружке? [3, c.14]
8. Ученик начертил 10 параллелограммов, среди них оказалось 6 ромбов, 5 прямоугольников и 3 квадрата. Есть ли среди начерченных параллелограммов фигуры, которые не являются ни ромбами, ни прямоугольниками? Если есть, то сколько их?
Теоретический материал
Обозначения:
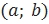 – упорядоченная пара, образованная из элементов
– упорядоченная пара, образованная из элементов 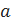 и
и 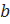 ;
;
А×В – декартово произведение множеств A и B;
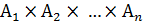 – декартово произведение множеств
– декартово произведение множеств 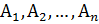 ;
;
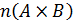 – количество элементов в декартовом произведении множеств A и B;
– количество элементов в декартовом произведении множеств A и B;
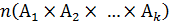 – количество элементов в декартовом произведении множеств
– количество элементов в декартовом произведении множеств 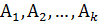 .
.
Элемент 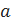 – первая координата (компонента) пары; элемент
– первая координата (компонента) пары; элемент 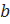 – вторая координата (компонента) пары.
– вторая координата (компонента) пары.
Декартово произведение множеств А и В (А×В) – множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента – множеству В.
Кортеж – упорядоченный набор 3 и более элементов.
Декартово произведение множеств 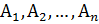 (
( 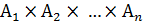 ) – множество всех кортежей длины n, первая компонента которых принадлежит множеству А1, вторая – множеству А2, …, n-я – множеству Аn.
) – множество всех кортежей длины n, первая компонента которых принадлежит множеству А1, вторая – множеству А2, …, n-я – множеству Аn.
Способы представления декартова произведения множеств:
а) перечисление элементов;
б) граф;
в) таблица;
г) на координатной плоскости.
Число элементов в декартовом произведении конечных множеств:
Два множества: 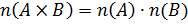 .
.
k множеств: 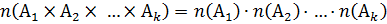 .
.
Задания
1. Найти декартово произведение множеств:
а) 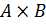 и
и 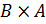 :
: 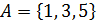 ,
, 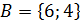 ;
;
б) 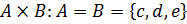 ;
;
в) 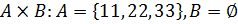 ;
;
г) 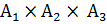 :
: 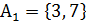 ,
, 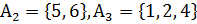 .
.
2. Представьте в виде графа и таблицы декартово произведение множеств 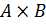 ,
, 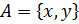 ,
, 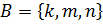 .
.
Таблица:
Граф:
3. Изобразите на координатной плоскости декартово произведение 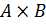 , если:
, если:
а) 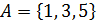 ,
, 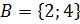 ;
;
б) 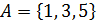 ,
, 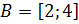 ;
;
в) 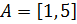 ,
, 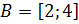 ;
;
г) 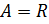 ,
, 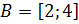 .
.
4. Сколько чисел можно составить из цифр 7, 8, 9, если:
а) числа двузначные, цифры в записи числа не повторяются;
б) числа двузначные, цифры в записи числа могут повторяться;
в) числа трехзначные, цифры в записи числа не повторяются;
г) числа трехзначные, цифры в записи числа могут повторяться.
5. Сколько чисел можно составить из цифр 5, 4, 0, если:
а) числа двузначные, цифры в записи числа не повторяются;
б) числа двузначные, цифры в записи числа могут повторяться;
в) числа трехзначные, цифры в записи числа не повторяются;
г) числа трехзначные, цифры в записи числа могут повторяться.
6. Запишите множество дробей, числителем которых являются числа из множества 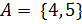 , а знаменателем – числа из множества
, а знаменателем – числа из множества 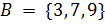 .
.
7. 3апишите различные двузначные числа, используя цифры 1, 3, 5, 7. Сколько среди них чисел, запись которых начинается с цифры 5? Переформулируйте эту задачу, используя понятие декартова произведения множеств.
Теоретический материал
Объем понятия – это множество всех объектов, обозначаемых одним термином.
Содержание понятия – это множество всех существенных свойств объекта, отраженных в этом понятии.
Если увеличивается объем понятия, то уменьшается его содержание, и наоборот.
Пусть заданы два понятия 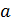 и
и 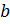 , имеющие объемы соответственно
, имеющие объемы соответственно 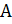 и
и 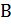 . Если
. Если 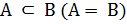 , то говорят, что понятие
, то говорят, что понятие 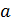 – видовое по отношению к понятию
– видовое по отношению к понятию 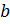 , а понятие
, а понятие 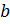 – родовое по отношению к
– родовое по отношению к 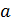 .
.
Если А = В, то говорят, что понятия 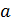 и
и 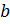 тождественны.
тождественны.
Операции с понятиями:
1. Обобщение понятия.
2. Ограничение понятия.
3. Деление понятия.
4. Определение понятия.
Определение понятия через род и видовое отличие
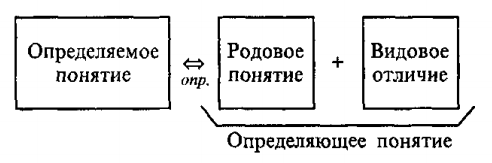
Правила определения понятий:
1. Соразмерность определения.
2. Отсутствие порочного круга в определении.
3. Ясность определения.
Неявные определения:
1. Контекстуальные.
2. Остенсивные.
Задания
1. Выберите пары понятий, которые находятся в отношении рода и вида:
а) многоугольник и треугольник;
б) угол и острый угол;
в) луч и прямая;
г) ромб и квадрат;
д) круг и окружность;
е) трехзначное число и двухзначное число.
_____________________________________________________________
_____________________________________________________________
2. Назовите пять существенных свойств понятия «равнобедренный треугольник» и изобразите с помощью кругов Эйлера отношение между объемом данного понятия и объемом понятия «остроугольный треугольник». [3, c.25]
Находятся ли понятия «остроугольный треугольник» и «равнобедренный треугольник» в отношении рода и вида?
Свойства:
1. ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
2. ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
3. ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
4. ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
5. ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
3. Выделите в определении «Высотой треугольника, проведенной из данной вершины, называют отрезок перпендикуляра между этой вершиной и прямой, содержащей противолежащую сторону» определяемое и определяющее понятие, родовое понятие (по отношению к определяемому) и видовое отличие.
Определяемое понятие:_________________________________________
_____________________________________________________________
_____________________________________________________________
Определяющее понятие:________________________________________
_____________________________________________________________
_____________________________________________________________
Родовое понятие:______________________________________________
_____________________________________________________________
_____________________________________________________________
Видовое отличие:______________________________________________
_____________________________________________________________
_____________________________________________________________
4. Сформулируйте понятие прямоугольника, используя в качестве родового понятия не менее двух различных понятий. Какие видовые отличия необходимо указать в каждом случае?
а) Определение:_______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Родовое понятие:______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Видовое отличие:______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
б) Определение:_______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Родовое понятие:______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Видовое отличие:______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
в) Определение:________________ _______________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________<
