Представление целых чисел в ЭВМ

Для представления целых чисел со знаком в ЭВМ используют прямой, обратный и дополнительный коды. При этом положительные числа во всех кодах представляются одинаково. Для дальнейшего изложения будем считать, что n = 4. В этом случае, существует 16 различных двоичных комбинаций, представленных в таблице 2. В таблице 3 эти комбинации рассмотрены для знакового представления чисел. Старший знаковый разряд выделен в таблице жирным шрифтом.

Прямой код числа формируется по следующему правилу: в знаковый разряд записывается знак числа, а в цифровые разряды – модуль числа. Несмотря на то, что данный код является наиболее простым и наглядным в нем нельзя выполнять операцию сложения отрицательных чисел или чисел с разным знаком. Например, сложение чисел +7 и -6 в прямом коде дает неверный результат:

0111 (+7)

+ 1110 (-6)

0101 (+5). Следовательно, надо переходить к другим кодам, а именно, к обратному и дополнительному кодам.

Для перевода отрицательного числа из прямого в обратный код необходимо в знаковый разряд числа записать 1, а в цифровой части числа инвертировать все разряды (заменить 0 на 1, а 1 на 0). Выполним предыдущую операцию сложения чисел в обратном коде:

0111 (+7)

+ 1001 (-6)

1 0000

+

0001 (+1).

Результат сложения – правильный, однако при сложении чисел в обратном коде единицу переноса из знакового разряда надо прибавлять к младшему разряду полученной суммы, а это лишняя машинная операция.

Таблица 3 - Представление чисел от -7 до +7 в машинных кодах

(10)	Прямой код	Обратный код	Дополнительный код
+1 +2 +3 +4 +5 +6 +7 -0 -1 -2 -3 -4 -5 -6 -7	0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111	0000 0001 0010 0011 0100 0101 0110 0111 1111 1110 1101 1100 1011 1010 1001 1000	0000 0001 0010 0011 0100 0101 0110 0111 0000 1111 1110 1101 1100 1011 1010 1001

Для перевода отрицательного числа из прямого в дополнительный код необходимо в знаковый разряд числа записать 1, в цифровой части числа инвертировать все разряды, после чего к младшему разряду результата добавить 1. Выполним операцию сложения чисел +7 и -6 в дополнительном коде:

0111 (+7)

+ 1010 (-6)

1 0001 (+1). При сложении чисел в дополнительном коде перенос из знакового разряда не учитывается. Результат сложения – правильный - +1.

В настоящее время в подавляющем большинстве ЭВМ для представления целых чисел со знаком используется дополнительный код. По сравнению с обратным кодом действия в дополнительном коде выполняются быстрее в силу следующих причин:

· не надо прибавлять перенос, возникающий в знаковом разряде;

· дополнительный код – единственный код, который имеет одно изображение ноля (таблица 3), т.е. при выполнении операции перехода проверка на ноль выполняется только один раз.

Следует также отметить, что комбинация 1000, отсутствующая в таблице 3, используется в дополнительном коде для представления числа -8.

Таким образом, диапазон представления целых чисел в формате со знаком для n = 4 составит от -8 до +7, а при произвольном n - от -2^n-1 до 2^n-1 -1.

Для представления отрицательных чисел в дополнительном коде в восьмеричной и шестнадцатеричной системах счисления необходимо каждую цифру в восьмеричном или шестнадцатеричном кодах заменить на взаимно обратную, после чего к младшему разряду добавить 1.

Взаимно обратными называются цифры, сумма которых равна q – 1, где q – основание системы счисления. Для двоичной системы взаимно обратными являются цифры 0 и 1. Приведем взаимно обратные цифры для других систем счисления:

а) для восьмеричной системы:

0 1 2 3 4 5 6 7

7 6 5 4 3 2 1 0;

б) для шестнадцатеричной системы:

0 1 2 3 4 5 6 7 8 9 A B C D E F

F E D C B A 9 8 7 6 5 4 3 2 1 0.

Пример. A = 17(16). Определить число –A, т.е перевести число A в дополнительный код.

E8 + 1 = E9.

2. ПРИМЕР ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

Выполнение задания рассмотрим на конкретном примере, предположив, что предпоследней цифре шифра соответствует число A1 = 90 (10), а последней – число A2 = 33 (10).

Для выполнения задания необходимо выполнить следующую последовательность действий:

1. Cформировать число W в десятичной системе. W = 90,33 (10).

2. Для перевода числа W в другие системы необходимо воспользоваться отдельно правилами перевода целой и дробной части числа (число A1 – целое, а число A2 – дробное).

Перевод в двоичную систему.

а) целой части б) дробной части

90 2 0,33

90 45 2 2

0 44 22 2 0,66

1 22 11 2 2

0 10 5 2 1,32

1 4 2 2 2

1 2 1 0,64

0 2

1,28

2

0,56

2

1,12

W =1011010,010101 (2). Проверим правильность перевода:

+

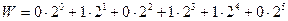
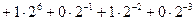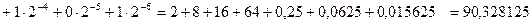(10).

Перевод в восьмеричную систему.

а) целой части б) дробной части

90 8 0,33

88 11 8 8

2 8 1 2,64

3 8

5,12

W =132,25 (8). Проверим правильность перевода:

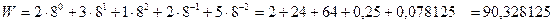(10).

Перевод в шестнадцатеричную систему.

а) целой части б) дробной части

90 16 0,33

80 5 16

10 5,28

16

4,48

W =5A,54 (16). Проверим правильность перевода:

(10).

Заметим, что дробная часть исходного числа и дробная часть, получаемая при переводе в десятичную систему из двоичной, восьмеричной и шестнадцатеричной систем отличается на 0,001875, что обусловлено заданной точностью перевода.

Поскольку двоичная система связана с восьмеричной и шестнадцатеричной специальными соотношениями (8 = 2³,16 = 2⁴), то выполнив перевод из десятичной системы в двоичную, можно выполнить перевод в восьмеричную систему (разбивая двоичное число на триады) и в шестнадцатеричную систему (разбивая число на тетрады).

W = 0 0 1 0 1 1 0 1 0 , 0 1 0 1 0 1 (2)

1 3 2 , 2 5 (8)

W = 0 1 0 1 1 0 1 0 , 0 1 0 1 0 1 0 0 (2)

5 A , 5 4 (16).

3. Представим числа в дополнительном коде.

3.1 Для двоичной системы

A1 = 1011010 (2). + A1 = 0 | 1011010.

- A1 = 1 | 0100101 (инвертируем разряды)

+ 1 (добавляем 1 к младшему разряду)

1 | 0100110.

Переведем целое число A2 в двоичную, восьмеричную и шестнадцатиричную системы счисления (также как мы переводили число A1) .

A2 = 33 (10) = 100001 (2) = 41 (8) = 21 (16).

Так как число A2 меньше числа A1, а операции над числами выполняются в фиксированном формате, то в качестве базового выбираем формат, имеющий число разрядов, необходимое для представления числа A1, а в старшую часть числа A2 для выравнивания добавляем незначащие нули, если это необходимо.

A2 = 0100001 (2). + A2 = 0 | 0100001.

- A2 = 1 | 1011110 (инвертируем разряды)

+ 1 (добавляем 1 к младшему разряду)

1 | 1011111.

В этом примере для представления чисел в двоичной системе счисления требуется 8 двоичных разрядов, включая знаковый разряд, т.е. можно сказать, что используется формат байта.

Следовательно, в восьмеричной системе для представления чисел потребуется три разряда, а в шестнадцатеричной – два.

3.2 Для восьмеричной системы:

A1 = 132 (8). + A1 = 132.

- A1 = 645 (заменяем цифры на взаимно обратные)

+ 1 (добавляем 1 к младшему разряду)

646.

A2 = 41 (8). + A2 = 041.

- A2 = 736 (заменяем цифры на взаимно обратные)

+ 1 (добавляем 1 к младшему разряду)

737.

3.3 Для шестнадцатиричной системы:

A1 = 5A (16). +A1 = 5A.

- A1 = A5 (заменяем цифры на взаимно обратные)

+ 1 (добавляем 1 к младшему разряду)

A6.

A2 = 21 (16). + A2 = 21.

- A2 = DE (заменяем цифры на взаимно обратные)

+ 1 (добавляем 1 к младшему разряду)

DF.

4. Выполним операции сложения над числами в двоичной, восьмеричной и шестнадцатеричной системах:

4.1 В двоичной системе:

A1 + A2 = 0 | 1011010 -A1 – A2 = 1 | 0100110

+ 0 | 0100001 1 | 1011111

0 | 1111011 (2) 1| 0000101 (2)

A1 - A2 = 0 | 1011010 -A1 + A2 = 1 | 0100110

+ 1 | 1011111 0 | 0100001

0 | 0111001 (2) 1| 1000111 (2) .

4.2 В восьмеричной системе:

A1 + A2 = 132 -A1 – A2 = 646

+ 041 737

173 (8) 605 (8)

A1 - A2 = 132 -A1 + A2 = 646

+ 737 041

071 (8) 707 (8) .

4.3 В шестнадцатеричной системе:

A1 + A2 = 5A -A1 – A2 = A6

+ 21 DF

7B (16) 85 (16)

A1 - A2 = 5A -A1 + A2 = A6

+ DF 21

3 9 (16) C7 (16) .

Заметим, что так как A1 + A2 = - (-A1 - A2) и A1 - A2 = - (A2 – A1), то вместо четырех действий в каждой системе можно было выполнить только два, а остальные два результата получить, используя перевод в дополнительный код. Например, для системы с основанием 16 имеем:

A1 + A2 = 7B (16) -A1 – A2 = 84

+ 1

85 (16) .

Покажем, что для операции A1 – A2 действия во всех системах счисления приводят к одному и тому же результату, используя перевод в десятичную систему.

A1 – A2 = 90 – 33 = 57 (10).

A1 – A2 = 0111001 (2) = 1 + 8 + 16 + 32 = 57 (10).

A1 – A2 = 071 (8) = 1 + 56 = 57 (10).

A1 – A2 = 039 (16) = 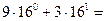9 + 48 = 57 (10).

5. Проверим полученные результаты на наличие арифметического переполнения.

Так как в нашем примере знаковые числа представляются в формате байта, то допустимый диапазон представления чисел в десятичной системе составляет от -128 до + 127. В рассмотренном примере при сложении чисел арифметического переполнения не возникает