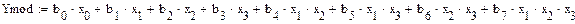Определим доверительные интервалы.
Доверительный интервал – интервал, построенный с помощью случайной выборки из распределения с неизвестными параметром, такой, что он содержит данный параметр с заданной вероятностью.
Левая граница доверительного интервала коэффициента 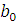 :
:
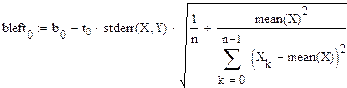
Правая граница доверительного интервала коэффициента 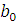 :
:
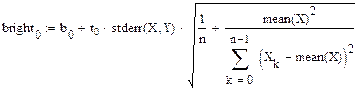
Нахождение доверительного интервала для коэффициента 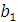 .
.
Левая граница доверительного интервала коэффициента 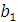 :
:
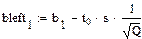
Правая граница доверительного интервала коэффициента 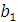 :
:
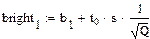 , где
, где
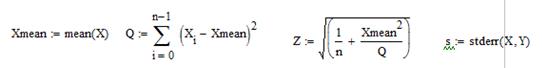
Нахождение доверительного интервала для дисперсии оценки:

Нахождение доверительной области для всей линии регрессии:

Теперь можно построить полученное уравнение регрессии с учетом доверительных интервалов.
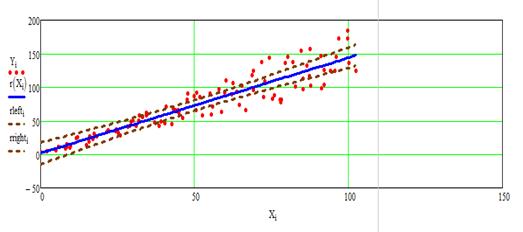
Рисунок 6 – Уравнение регрессии с доверительной областью
Вывод.
Регрессионный анализ – статистический метод исследования, позволяющий определять степень детерминированности вариации зависимых переменных от независимых. Уравнение регрессии отображает зависимость между результативным и факторным признаками, позволяет предсказывать возможные значения исследуемой функции.
Лабораторная работа 2.
План эксперимента удобно задавать таблицей, называемой матрицей планирования эксперимента, включающей в себя последовательность проведения опытов, значения факторов и эффектов их взаимодействий, а также значения исследуемой функции, называемой функцией отклика.
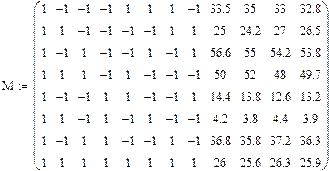
В матрице представлены следующие вектор-столбцы: первый - фиктивной переменной, во всех опытах его значение равно +1, второй-четвертый – являются линейными коэффициентами, пятый-восьмой – эффекты взаимодействия линейных коэффициентов, девятый-двенадцатый – значения функции отклика, полученные в результате проведения экспериментов.
Обработка результатов эксперимента.
План статистической обработки результатов законченного эксперимента:
1. Нахождение дисперсии воспроизводимости.
2. Проверка значимости отдельных коэффициентов регрессии.
3. Определение оценки дисперсии адекватности.
4. Проверка адекватности полученной математической модели.
Находим среднеквадратическое отклонение:
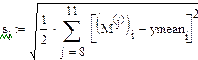
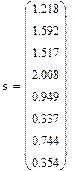
Пользоваться построчными средними для определения коэффициентов полинома можно, только если построчные дисперсии являются однородными. При равномерном дублировании опытов однородность ряда построчных дисперсий определяется по критерию Кохрена. Из таблицы (Рис №5) определим значение G-критерия для уровня значимости α=0.05 чисел степеней свободы f1 – количество опытов для каждого плана - 1 и f2 – число экспериментов.
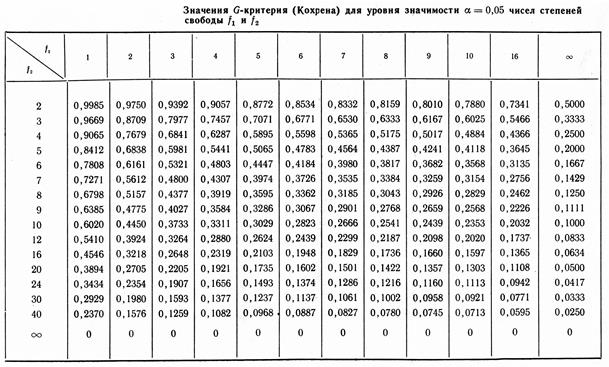
Рисунок 7 – Таблица Кохрена
f1 = 4-1=3, f2 =8:
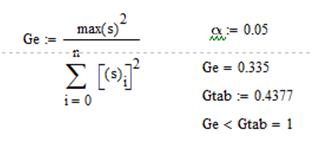
Так как Ge<Gtab, то ряд дисперсий считается однородным и значит, использование построчных средних допустимо.
Воспользуемся строчной средней для нахождения коэффициентов модели:
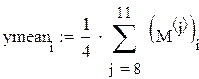
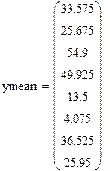
Находим коэффициенты модели:
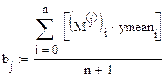
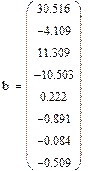
Получаем полнофакторную модель: