Тема: «Плоская система сходящихся сил»».
Цели:
1) Научиться расставлять активные и реактивные силы.
2) Научиться составлять расчетную схему.
3) Научиться определять усилие в стержнях системы аналитическим путем.
Время выполнения:7 часов.
Для выполнения задания необходимо знать:
Связи и их реакции.
Свободное тело — это тело, движению которого ничто не препятствует. Несвободное тело — это тело, движению которого препятствуют другие тела. Связь — это тело, которое препятствует движению других тел. Реакция связи — это сила, с которой связь действует на тело, препятствуя его движению.

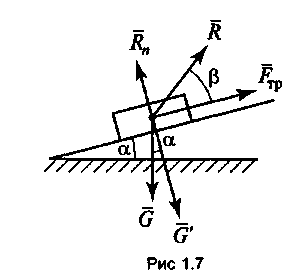
Рисунок 1. Рисунок 2.
Существуют шесть основных типов связи:
1) в виде гладкой поверхности (поверхность стола, ровной дороги). Реакция связи направлена перпендикулярно поверхности связи (рис 1.);
2) в виде шероховатой поверхности. Условно изображается наклонной плоскостью (рис 2.). Полная реакция связи R направлена под углом β (Rn — нормальная реакция опоры);
3) в виде прямого жесткого стержня с шарнирным
закреплением концов. Реакция стержня направлена
вдоль его оси (рис 3, а);
4) в виде точечной опоры. Реакция направлена перпендикулярно поверхности опоры (рис 3, б);
5) в виде ребра двухгранного угла. Реакция направлена перпендикулярно поверхности тела опор (рис. 3, в);
6) в виде гибкой связи (ремень, канат, цепь). Реакция направлена вдоль связи (рис.3, г).
а)  б)
б) 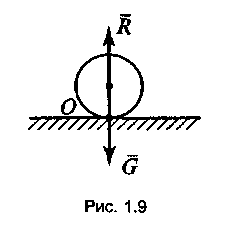
в) 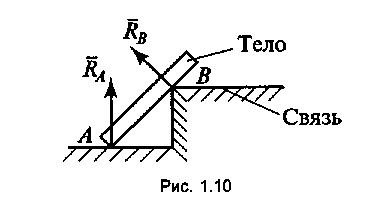 г)
г) 
Рисунок 3.
Плоская система сходящихся сил. Системы сил и условия их равновесия.
Плоской системой сходящихся сил называется система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке (рис. 4).
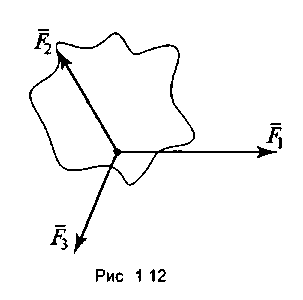
Рисунок 4.
Чтобы выяснить, будет ли данное тело находиться в равновесии под действием плоской системы сходящихся сил, необходимо найти ее равнодействующую силу. Если равнодействующая равна нулю, система находится в равновесии, если не равна нулю — не находится в равновесии. Существует два способа определения равнодействующей силы плоской системы сходящихся сил: геометрический и аналитический.
Геометрический способ определения равнодействующей — построение силового многоугольника: в произвольно выбранную точку переносится объект равновесия, в эту точку помещается начало первого вектора, перенесенного параллельно самому себе; к концу первого вектора переносится начало второго вектора, к концу второго — начало третьего и т.д.
Если построенный силовой многоугольник окажется незамкнутым, значит, данная система сил не находится в равновесии. В этом случае вектор равнодействующей силы соединит начало первого вектора с концом последнего (рис. 5, а).
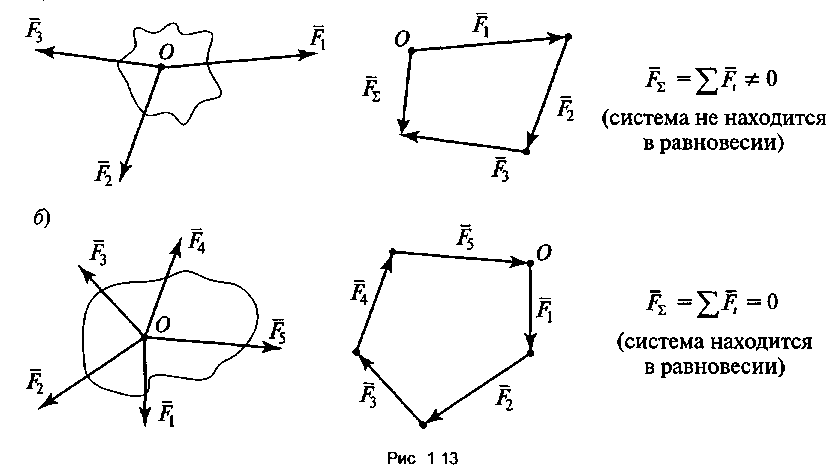
Рисунок 5.
Геометрическое условие равновесия плоской системы сходящихся сил заключается в замкнутости силового многоугольника, т.е. при построении силового многоугольника конец последнего вектора совпадает с началом первого (рис. 5, б).
Аналитический способ определения равнодействующей: все силы проектируются на две взаимно перпендикулярные оси координат, а затем находится алгебраическая сумма проекций всех сил на ось х и ось у. Если алгебраическая сумма проекций всех сил равна нулю, данная система сил находится в равновесии. Аналитическое условие равновесия плоской системы сходящихся сил:
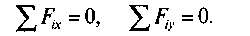 (1)
(1)
Осью координат называется произвольно выбранный направленный отрезок прямой (рис. 6).

Рисунок 6.
Проекция силы на ось координат — отрезок оси, отсекаемый перпендикулярами, опущенными из начала и конца вектора (рис. 7).
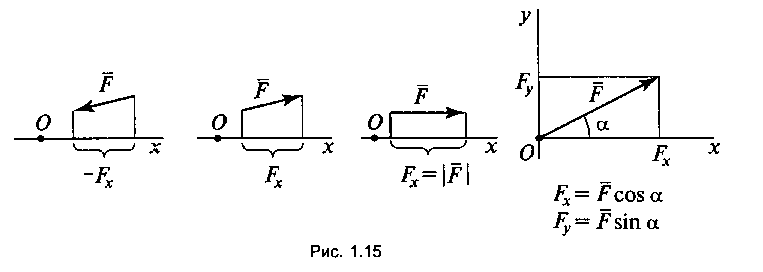
Рисунок 7.
Методические рекомендации к выполнению задания №2.
1) Внимательно прочитать условие задачи, записать, что дано и что требуется определить.
2) Расставить все активные и реактивные силы.
3) Составить расчетную схему.
4) Составить и решить уравнения проекций сил системы на оси х и у согласно условию (1).
5) Написать ответ.
6) Выполнить графическое решение методом силового многоугольника (рис.5).
7) Написать ответ.
8) Сравнить результаты аналитического и графического методов решения через погрешность результатов. Отклонение не должно превышать 5 %.
Пример решения задания.
Определить усилия в стержнях кронштейна (рис.8) от приложенной внешней силы. Трением в блоке пренебречь. Данные для задачи своего варианта взять из таблицы.
Дано: F = 50 кН; a = 45°; b = 50°; g = 60°
Определить: R1 и R2.
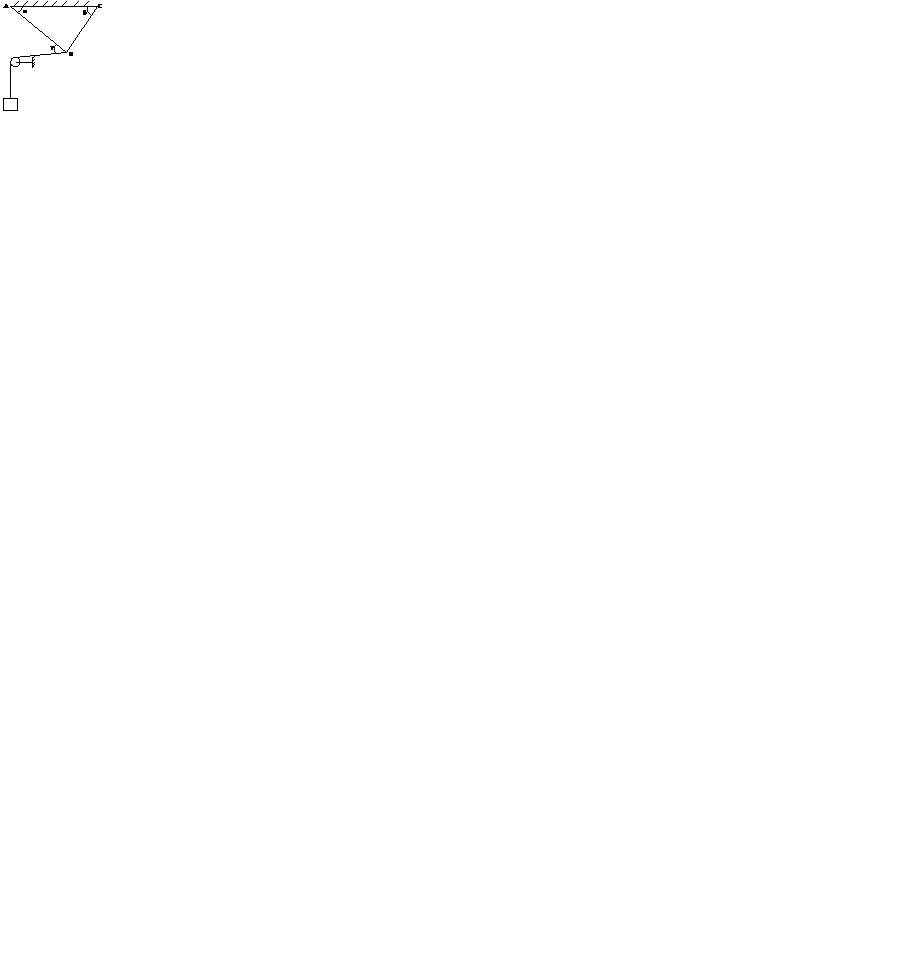
Рисунок 8.
Решение:
1) Составим расчетную схему (рис. 9)
2) Составим уравнения проекций сил системы на оси х и у согласно условию (1):
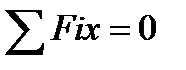 ;
; 
 ;
; 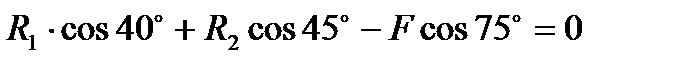
3) Решим их относительно неизвестных R1 и R2:
из 1-го уравнения:
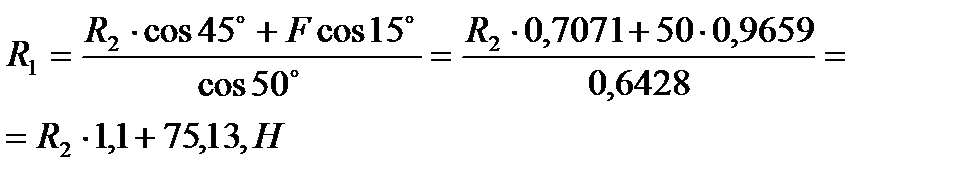

Рисунок 9.
Подставим найденное значение R1 во второе уравнение:
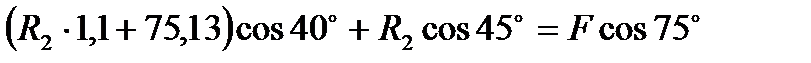
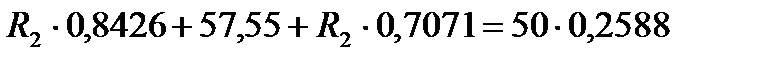
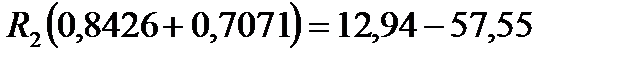
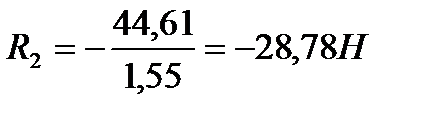
Следовательно R1 будет равно:

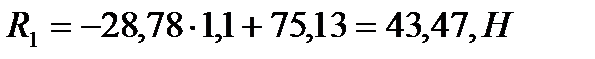
Ответ: R1 = 43,47 Н; R2 = - 28,78 Н
Знак «-» в реакции R2 получился из-за того, что первоначально направление реакции было выбрано ошибочно.
Задание.
Определить усилия в стержнях кронштейна от приложенной внешней силы (рис. 10). Трением в блоке пренебречь. Данные для своего варианта взять из таблицы 1.
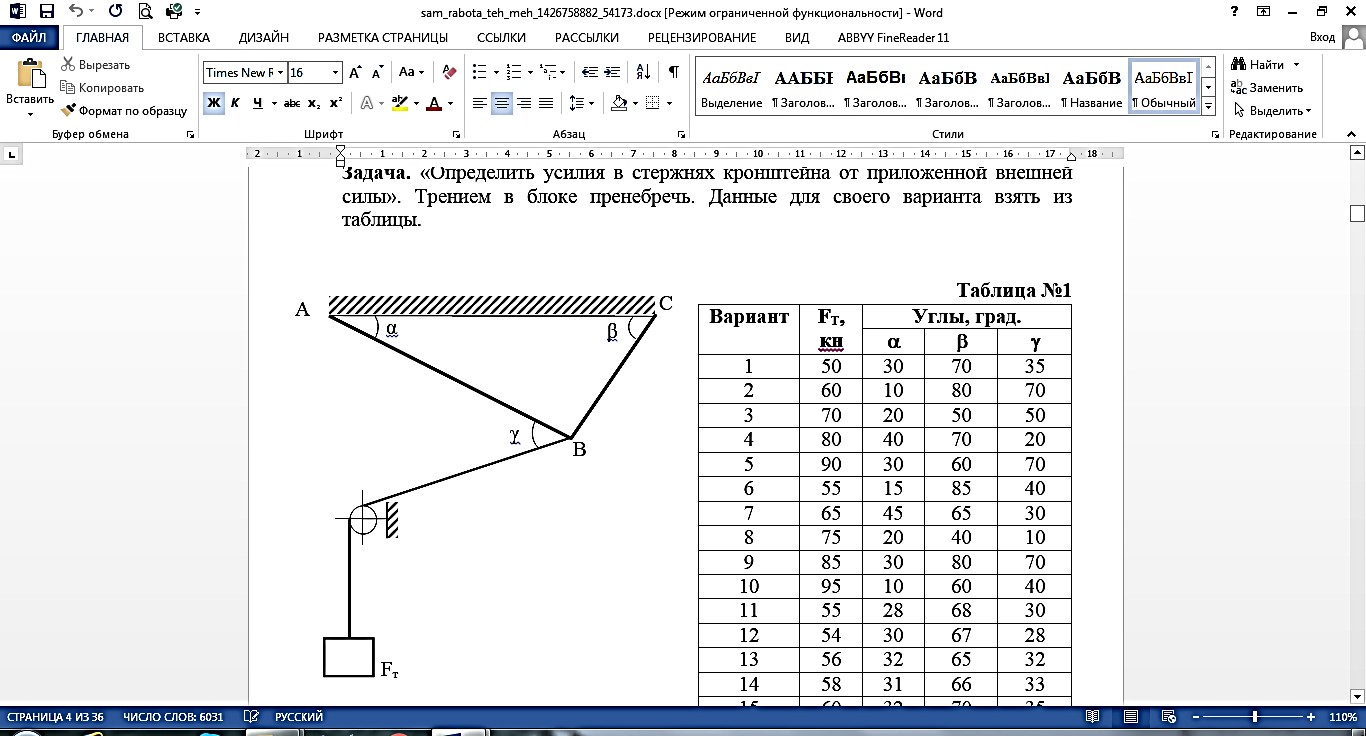
Рисунок 10.
Таблица 1.
| Вариант | FТ, кН | Углы, град. | Вариант | FТ, кН | Углы, град. | ||||
| a | b | g | a | b | g | ||||
Расчетно-практическая работа №2.
