Метод вращений Якоби решения симметричной полной проблемы собственных значений
Метод вращений Якоби предполагает решение полной проблемы собственных значений для симметричных вещественных матриц. Для таких матриц собственные вектора образуют полную ортонормированную систему, т.е. пользуясь обозначениями, введенными в свойстве 6 предыдущего раздела, можно записать:
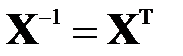 ,
, 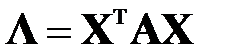 (1.4)
(1.4)
Значит, для всякой симметричной матрицы А найдется диагональная матрица 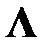 , ей ортогонально подобная. Приближенно реализовать равенство (1.4), т.е. найти сразу все собственные числа матрицы А (элементы диагонали матрицы
, ей ортогонально подобная. Приближенно реализовать равенство (1.4), т.е. найти сразу все собственные числа матрицы А (элементы диагонали матрицы 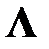 ) и все соответствующие им собственные векторы (столбцы матрицы X), позволяет применение к А последовательности однотипных преобразований, сохраняющих спектр и приводящих в пределе данную матрицу к диагональному виду.
) и все соответствующие им собственные векторы (столбцы матрицы X), позволяет применение к А последовательности однотипных преобразований, сохраняющих спектр и приводящих в пределе данную матрицу к диагональному виду.
Для этих целей используются преобразования с помощью так называемой матрицы плоских вращений:
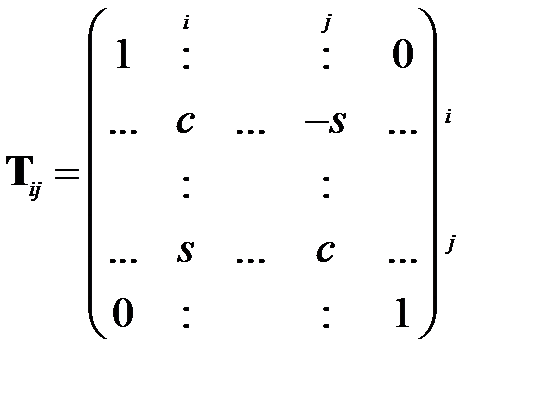 (1.5)
(1.5)
Она получается из единичной матрицы заменой двух единиц и двух нулей на пересечениях i-x и j-x строк и столбцов числами с и 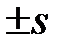 , как показано в (1.5), такими, что
, как показано в (1.5), такими, что
1. 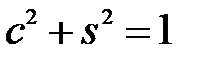 . (1.6)
. (1.6)
Условие нормировки (1.6) позволяет интерпретировать числа c и s как косинус и синус некоторого угла 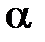 , и, так как умножение любой матрицы на матрицу
, и, так как умножение любой матрицы на матрицу 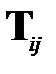 изменяет у нее только две строки и два столбца по формулам поворота на угол
изменяет у нее только две строки и два столбца по формулам поворота на угол 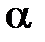 в плоскости, отделяемой выбранной парой индексов i и j, то это объясняет название матрицы
в плоскости, отделяемой выбранной парой индексов i и j, то это объясняет название матрицы 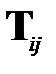 .
.
Матрица 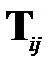 ортогональна при любых
ортогональна при любых 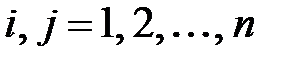 , и значит, матрица
, и значит, матрица
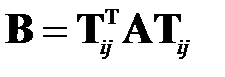 (1.7)
(1.7)
подобна А, т.е. имеет тот же набор собственных чисел, что и матрица А.
Классический итерационный метод вращений, предложенный Якоби (1846 г.), предполагает построение последовательности матриц
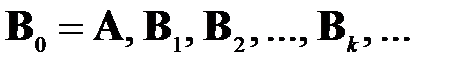
с помощью преобразований типа (1.7)
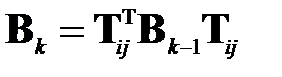 (1.8)
(1.8)
такой, что на 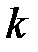 -м шаге обнуляется максимальный по модулю элемент матрицы
-м шаге обнуляется максимальный по модулю элемент матрицы 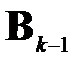 предыдущего шага (а значит, и симметричный ему элемент). Эта стратегия определяет способ фиксирования пары индексов i, j, задающих позиции
предыдущего шага (а значит, и симметричный ему элемент). Эта стратегия определяет способ фиксирования пары индексов i, j, задающих позиции 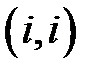 ,
, 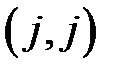 ,
, 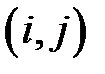 ,
, 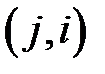 «существенных» элементов в матрице вращения
«существенных» элементов в матрице вращения 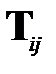 , и угол поворота
, и угол поворота 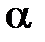 , конкретизирующий значения этих элементов: .
, конкретизирующий значения этих элементов: . 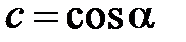 .и
.и 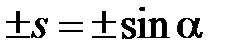 . На каждом шаге таких преобразований пересчитываются только две строки (или два столбца, что неважно в силу симметрии) матрицы предыдущего шага.
. На каждом шаге таких преобразований пересчитываются только две строки (или два столбца, что неважно в силу симметрии) матрицы предыдущего шага.
Пусть 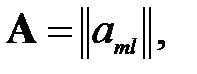
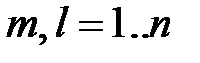 – исходная симметричная матрица, а
– исходная симметричная матрица, а 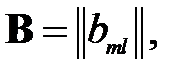
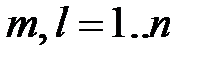 – матрица, получающаяся после одного шага преобразований по формуле (1.7). Обозначим через
– матрица, получающаяся после одного шага преобразований по формуле (1.7). Обозначим через 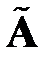 и
и 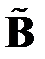 двумерные подматрицы этих матриц, определяемые фиксированием позиции
двумерные подматрицы этих матриц, определяемые фиксированием позиции 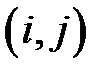 некоторого элемента
некоторого элемента 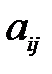 матрицы
матрицы 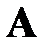 :
:
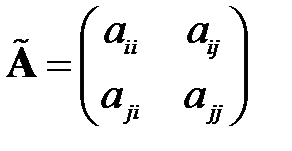 ,
, 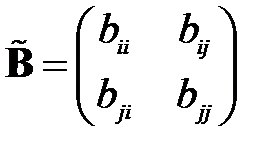 ,
,
а через 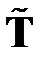 – такую же подматрицу матрицы
– такую же подматрицу матрицы 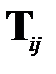 :
:
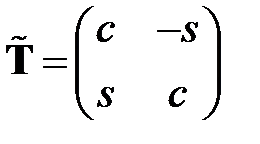 .
.
Очевидно, что равенство (1.7), записанное для матриц А, В, 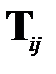 , будет верным и для их подматриц
, будет верным и для их подматриц 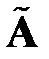 ,
, 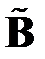 ,
, 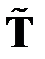 . Рассчитаем с его помощью элементы матрицы
. Рассчитаем с его помощью элементы матрицы 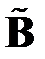 :
:
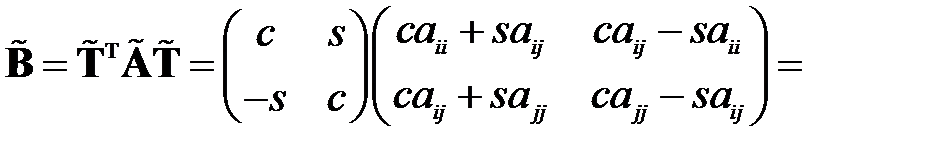
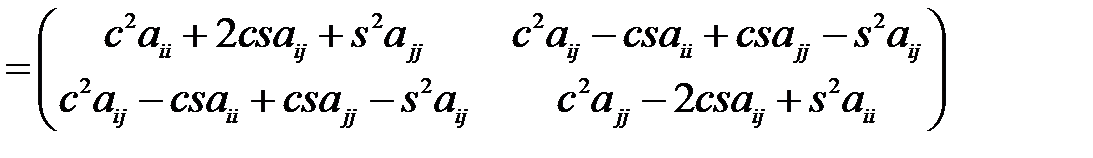 .
.
Очевидно, что 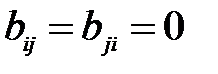 , если
, если 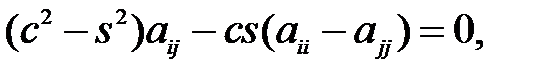 т.е. если
т.е. если
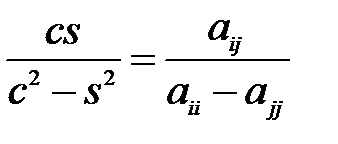 .
.
Учитывая тригонометрическую интерпретацию чисел 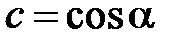 и
и 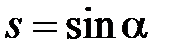 , в соответствии с чем можно считать
, в соответствии с чем можно считать
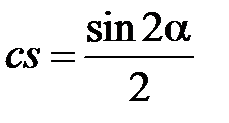 ,
, 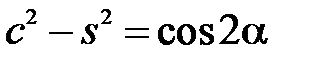 ,
,
приходим к выводу, что матрица В будет иметь нулевые внедиагональные элементы 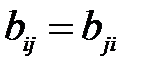 , если использовать преобразование плоского вращения по формуле (1.7) на угол
, если использовать преобразование плоского вращения по формуле (1.7) на угол 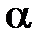 такой, что
такой, что
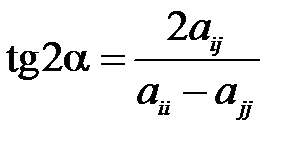 .
.
(для определенности считают 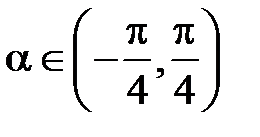 ).
).
Находить непосредственно угол 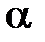 нет необходимости, поскольку нужные для выполнения преобразований числа с и s можно получить через значение
нет необходимости, поскольку нужные для выполнения преобразований числа с и s можно получить через значение 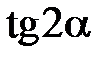 . На этой стадии метода предъявляются наибольшие требования к точности, так как искажение с и s нарушает ортогональность матриц Т, что ведет к неустранимым погрешностям (метод вращений, итерационный по форме, не является итерационным по существу: ему не присуща самоисправляемость методов последовательных приближений).
. На этой стадии метода предъявляются наибольшие требования к точности, так как искажение с и s нарушает ортогональность матриц Т, что ведет к неустранимым погрешностям (метод вращений, итерационный по форме, не является итерационным по существу: ему не присуща самоисправляемость методов последовательных приближений).
Нужно отметить, что описанный подход к решению полной проблемы собственных значений эффективен и тогда, когда исходная матрица имеет кратные и, что хуже, близкие собственные числа.
Пользуясь проделанными рассуждениями, запишем последовательность действий, определяющих один шаг метода вращений Якоби (каждый шаг состоит в расчёте матрицы 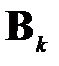 на основе
на основе 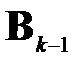 при помощи соотношения (1.8)):
при помощи соотношения (1.8)):
1. Выбирается ключевой элемент 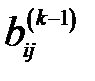 матрицы
матрицы 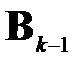 (стратегия его выбора рассматривается ниже).
(стратегия его выбора рассматривается ниже).
2. Вычисляется 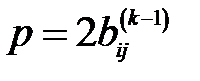 ,
, 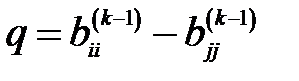 ,
, 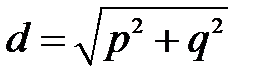 .
.
3. Вычисляются значения 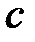 и
и 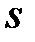 : Если
: Если 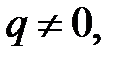 то
то 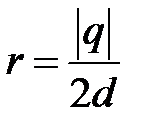 ,
, 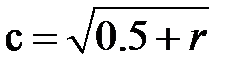 ,
, 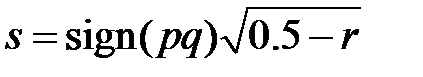 (если
(если 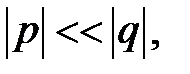 то лучше
то лучше 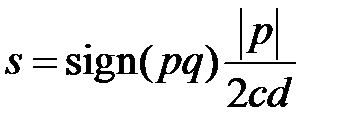 ), если же q=0, то
), если же q=0, то 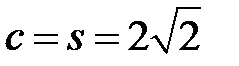 .
.
4. Вычисляются новые диагональные элементы матрицы 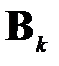 :
:
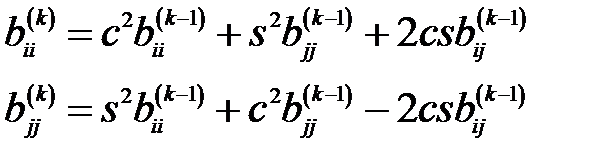
5. Внедиагональные элементы 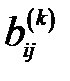 и
и 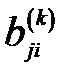 полагаются равными 0 (для контроля точности их значения можно вычислить по формуле:
полагаются равными 0 (для контроля точности их значения можно вычислить по формуле: 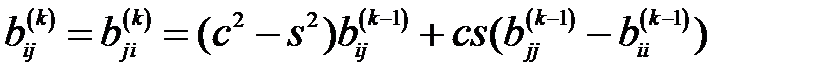 );
);
6. При 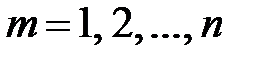 таких, что
таких, что 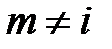 ,
, 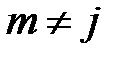 вычисляются изменяющиеся внедиагональные элементы:
вычисляются изменяющиеся внедиагональные элементы:
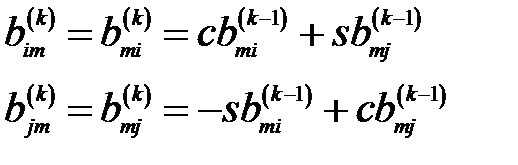
7. Для всех остальных пар индексов 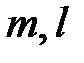 принимается
принимается 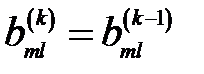 .
.
Вернёмся теперь к стратегии выбора ключевого элемента 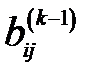 . На практике наиболее распространены два подхода:
. На практике наиболее распространены два подхода:
1. Классический, при котором в качестве ключевого элемента, определяющего индексы 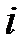 и
и  , принимается максимальный по модулю элемент матрицы
, принимается максимальный по модулю элемент матрицы 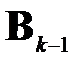 :
:
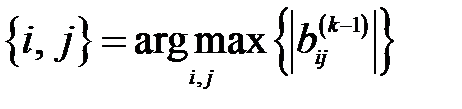 .
.
В [1] показано, что при таком способе выбора ключевого элемента последовательность подобных матриц 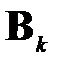 сходится к диагональной матрице
сходится к диагональной матрице 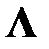 из собственных значений со скоростью геометрической прогрессии. Однако при больших величинах n его реализация наталкивается на существенные потери машинных ресурсов, связанные с поиском наибольшего по модулю ключевого элемента.
из собственных значений со скоростью геометрической прогрессии. Однако при больших величинах n его реализация наталкивается на существенные потери машинных ресурсов, связанные с поиском наибольшего по модулю ключевого элемента.
2. Метод барьеров. Стратегия выбора ключевого элемента здесь такова: устраивается циклический перебор всех над- или поддиагональных элементов матрицы 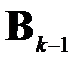 , но при этом пропускаются элементы, абсолютные величины которых меньше некоторого заданного положительного числа – барьера. Этот барьер может быть переменным (уменьшающимся по какому-либо осмысленному принципу). Сходимость метода несколько медленней, чем при классическом способе, но существенный выигрыш в быстродействии при выборе ключевого элемента оправдывает его практическое применение.
, но при этом пропускаются элементы, абсолютные величины которых меньше некоторого заданного положительного числа – барьера. Этот барьер может быть переменным (уменьшающимся по какому-либо осмысленному принципу). Сходимость метода несколько медленней, чем при классическом способе, но существенный выигрыш в быстродействии при выборе ключевого элемента оправдывает его практическое применение.
В завершение, остается вспомнить, что в соответствии со свойствами 6, 7 из предыдущего раздела и проведенными рассуждениями за собственные векторы 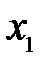 ,
, 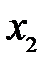 , …,
, …, 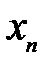 матрицы А (имеющие единичную евклидову норму) могут быть приближенно приняты столбцы результирующей матрицы, получающейся справа от А в цепочке преобразований подобия:
матрицы А (имеющие единичную евклидову норму) могут быть приближенно приняты столбцы результирующей матрицы, получающейся справа от А в цепочке преобразований подобия:
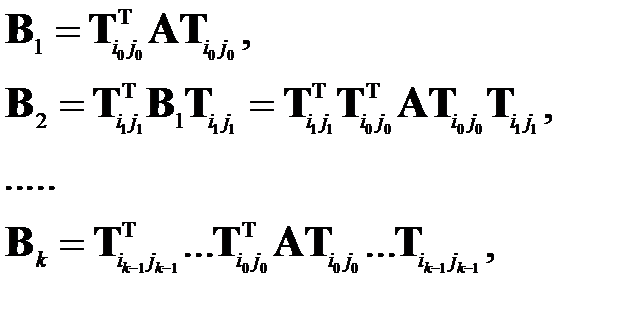
т.е. матрицы 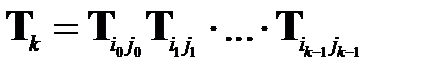 при некотором
при некотором 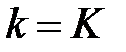 .
.
Критерием окончания процесса вращений Якоби может служить, например, достаточная малость модуля ключевого элемента на 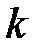 -ом шаге:
-ом шаге: 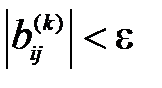 , где
, где 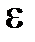 – некоторое малое число, определяющее допустимую погрешность вычислений метода.
– некоторое малое число, определяющее допустимую погрешность вычислений метода.
Литература
1. Амелькин Н.И. Кинематика и динамика твердого тела (кватернионное изложение). – М.: МФТИ (ГУ), 2000. – 64 с.
2. Бесекерский В. А., Попов Е.П. Теория Систем автоматического управления. – Изд. 4-е, перераб. и доп. – Спб.: Профессия, 2003. – 752 с.
3. Бобронников В. Т., Красильщиков М. Н., Козорез Д. А. и др. Статистическая динамика и оптимизация управления летательных аппаратов: учебное пособие. / Под общ. ред. М. Н. Красильщикова, В. В. Малышева. – Изд. 2-е, перераб. и доп. – М.: Альянс, 2013. – 468 с.
4. Бранец В. Н., Шмыглевский И. П. Применение кватернионов в задачах ориентации твердого тела. – М.: Наука, 1973. – 320 с.
5. Вержбицкий В.М. Основы численных методов: Учебник для вузов. – М.: Высшая школа, 2002. – 840 с.
6. Желтов С.Ю., Веремеенко К.К., Ким Н.В. и др. Современные информационные технологии в задачах навигации и наведения беспилотных маневренных летательных аппаратов. / Под ред. М.Н. Красильщикова, Г.Г. Себрякова. – М.: ФИЗМАТЛИТ, 2009. – 556 с.
7. Осипов Д.Л. – Delphi. Программирование для Windows, OS X, iOS и Android. – Спб.: БХВ-Петербург, 2014. – 464 с.
8. Рашевский П. К. Риманова геометрия и тензорный анализ. – М.: Наука, 1967. – 664 с.
9. Страуструп Б. Программирование: принципы и практика с использованием С++. – Второе издание. – М.: Вильямс, 2016. – 1328 с.
10. Умнов А. Е., Аналитическая геометрия и линейная алгебра: учебное пособие. – 3-е изд., испр. и доп. – М.: МФТИ, 2011. – 554 с.
11. Элджер Дж. С++: Библиотека программиста. – Спб.: Питер, 1999. – 320 с.
[1] Более подробно основные понятия и определения линейной алгебры рассматриваются, например, в [10].
[2] Строго говоря, такая интерпретация допустима и для 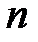 -мерного однородного гиперпространства, но в задачах моделирования процессов функционирования интегрированных систем ЛА такое обобщение, как правило, излишне.
-мерного однородного гиперпространства, но в задачах моделирования процессов функционирования интегрированных систем ЛА такое обобщение, как правило, излишне.
