Понятие и свойства собственных чисел и векторов
Нахождение собственных чисел и собственных векторов матриц – одна из наиболее сложных задач линейной алгебры, возникающих в процессе моделирования и анализа процессов функционирования динамических систем, статистического моделирования. Так, например, собственные векторы ковариационной матрицы случайного вектора определяют направления главных осей гиперэллипсоида рассеивания значений этого вектора, а собственные числа – растяжение или сжатие гиперэллипсоида по его главным осям. В механике собственные векторы и числа тензора инерции характеризуют направление главных осей и главные моменты инерции твёрдого тела.
Различают полную (алгебраическую или, иначе, матричную) проблему собственных значений, предполагающую нахождение всех собственных пар 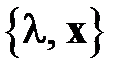 некоторой матрицы
некоторой матрицы  , и частичные проблемы собственных значений, состоящие, как правило, в нахождении одного или нескольких собственных чисел
, и частичные проблемы собственных значений, состоящие, как правило, в нахождении одного или нескольких собственных чисел  и, возможно, соответствующих им собственных векторов
и, возможно, соответствующих им собственных векторов 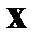 . Чаще всего, в последнем случае речь идет о нахождении наибольшего и наименьшего по модулю собственных чисел; знание таких характеристик матрицы позволяет, например, делать заключения о сходимости тех или иных итерационных методов, оптимизировать их параметры и т.д.
. Чаще всего, в последнем случае речь идет о нахождении наибольшего и наименьшего по модулю собственных чисел; знание таких характеристик матрицы позволяет, например, делать заключения о сходимости тех или иных итерационных методов, оптимизировать их параметры и т.д.
Задачу на собственные значения можно сформулировать так: для каких ненулевых векторов 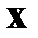 и чисел
и чисел  линейное преобразование вектора с помощью матрицы
линейное преобразование вектора с помощью матрицы 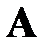 не изменяет направления этого вектора в пространстве, а сводится лишь «растяжению» этого вектора в
не изменяет направления этого вектора в пространстве, а сводится лишь «растяжению» этого вектора в 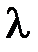 раз? Ответ на этот вопрос заключается в нетривиальных решениях уравнения
раз? Ответ на этот вопрос заключается в нетривиальных решениях уравнения
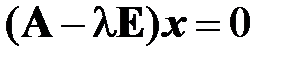 , (1.2)
, (1.2)
где  – единичная матрица. Теоретически эта задача легко решаема: нужно найти корни так называемого характеристического уравнения
– единичная матрица. Теоретически эта задача легко решаема: нужно найти корни так называемого характеристического уравнения
 (1.3)
(1.3)
и, подставляя их поочередно в (1.2), получать из соответствующих переопределенных систем собственные векторы.
Практическая реализация такого подхода сопряжена с рядом трудностей, возрастающих с ростом размерности решаемой задачи. Трудности эти обусловлены развертыванием определителя  и вычислением корней получающегося при этом многочлена n-й степени, а также поиском линейно независимых решений вырожденных систем линейных алгебраических уравнений. В связи с этим, такой непосредственный подход к решению алгебраической проблемы собственных значений обычно применяют лишь при очень малых размерах матриц
и вычислением корней получающегося при этом многочлена n-й степени, а также поиском линейно независимых решений вырожденных систем линейных алгебраических уравнений. В связи с этим, такой непосредственный подход к решению алгебраической проблемы собственных значений обычно применяют лишь при очень малых размерах матриц 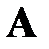 (n= 2, 3). Уже при n > 4 на первый план выходят специальные численные методы решения таких задач, один из которых, опирающийся на матричное преобразование подобия, будет рассмотрен далее. Напомним, что подобными называются матрицы
(n= 2, 3). Уже при n > 4 на первый план выходят специальные численные методы решения таких задач, один из которых, опирающийся на матричное преобразование подобия, будет рассмотрен далее. Напомним, что подобными называются матрицы  и
и 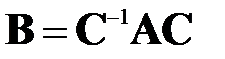 , где С – произвольная невырожденная матрица.
, где С – произвольная невырожденная матрица.
Перечислим кратко основные свойства собственных чисел и векторов:
1. Если 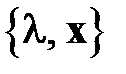 – собственная пара матрицы А, а
– собственная пара матрицы А, а  – некоторое число, то
– некоторое число, то 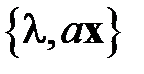 также является собственной парой для А. Это означает, что каждому собственному числу
также является собственной парой для А. Это означает, что каждому собственному числу 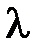 соответствует бесчисленное множество собственных векторов, различающихся лишь скалярным множителем.
соответствует бесчисленное множество собственных векторов, различающихся лишь скалярным множителем.
2. Пусть  – собственная пара матрицы
– собственная пара матрицы 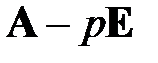 , где
, где 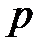 – некоторое действительное число. Тогда
– некоторое действительное число. Тогда 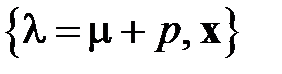 – собственная пара матрицы А. Таким образом, прибавление к данной матрице А диагональной матрицы
– собственная пара матрицы А. Таким образом, прибавление к данной матрице А диагональной матрицы  не изменяет ее собственных векторов и смещает спектр исходной матрицы на число
не изменяет ее собственных векторов и смещает спектр исходной матрицы на число 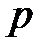 (влево при
(влево при 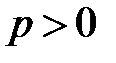 ). Спектром матрицы называется множество всех ее собственных значений.
). Спектром матрицы называется множество всех ее собственных значений.
3. Если  – собственная пара обратимой матрицы
– собственная пара обратимой матрицы 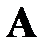 , то
, то 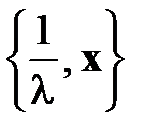 – собственная пара матрицы
– собственная пара матрицы  .
.
4. Собственными числами диагональных и треугольных матриц являются их диагональные элементы, т.к. характеристическое уравнение (1.3) с учётом (1.1) для таких матриц может быть записано в виде:
 .
.
Последнее равенство показывает, что диагональные и треугольные вещественные матрицы имеют только вещественные собственные значения (ровно n с учетом возможной их кратности). Вещественность собственных чисел присуща и очень важному в приложениях классу симметричных матриц, к числу которых относятся ковариационные матрицы и тензоры инерции.
5. Если  – собственная пара матрицы
– собственная пара матрицы  , то
, то  – собственная пара матрицы А Таким образом, преобразование подобия сохраняет неизменным спектр любой матрицы.
– собственная пара матрицы А Таким образом, преобразование подобия сохраняет неизменным спектр любой матрицы.
6. Пусть А – матрица простой структуры размерности 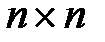 , а матрицы
, а матрицы  и
и  образованы из ее собственных чисел и собственных векторов соответственно. Тогда справедливо равенство
образованы из ее собственных чисел и собственных векторов соответственно. Тогда справедливо равенство 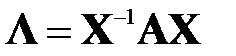 . Так как для диагональной матрицы
. Так как для диагональной матрицы  , образованной из собственных чисел, собственными векторами могут служить единичные векторы исходного базиса (
, образованной из собственных чисел, собственными векторами могут служить единичные векторы исходного базиса ( 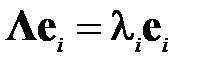 ,
, 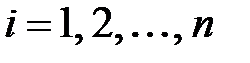 ), то, используя свойство 5 и принимая
), то, используя свойство 5 и принимая  и
и 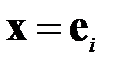 (т.е.
(т.е.  ), свойство 6 можно сформулировать иначе: если
), свойство 6 можно сформулировать иначе: если 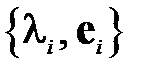 является собственной парой матрицы
является собственной парой матрицы  , то
, то 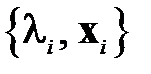 есть собственная пара матрицы А.
есть собственная пара матрицы А.
