Элементарные алгебраические операции над векторами и матрицами

Сложение векторов

Для сложения векторов определена процедура, состоящая в сложении их соответствующих элементов:

, , ,

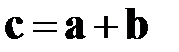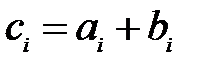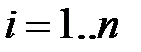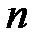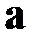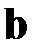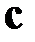где – количество элементов векторов , и , т.е. оба слагаемых должны обладать одинаковой размерностью.

Модуль и норма вектора

Нормой вектора называется число, равное сумме квадратов его элементов:

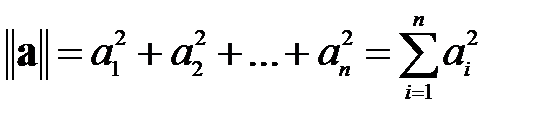
Модулем вектора называется число, равное квадратному корню из его нормы. При наличии геометрической интерпретации вектора это число характеризует его длину:

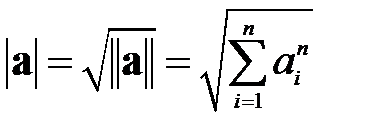
Скалярное произведение векторов

Скалярным произведением двух векторов в общем случае называется число, равное сумме произведений их соответствующих элементов:

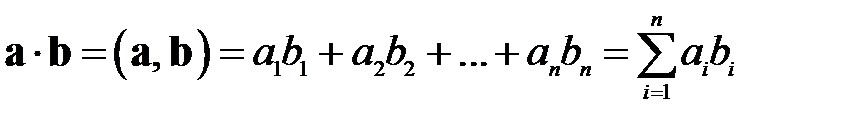
В частном случае, когда размерность множителей 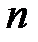равна трём и они допускают геометрическую интерпретацию, скалярное произведение векторов может быть вычислено как произведение их модулей на косинус угла между ними[2]:

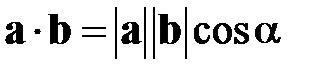
Скалярное произведение взаимно-ортогональных векторов равно нулю. Операция скалярного произведения обладает свойствами коммутативности, т.е. 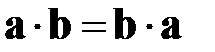и дистрибутивности: .

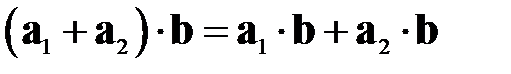Векторное произведение векторов

Векторным произведением двух неколлинеарных векторов 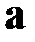и 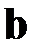, определённых в трёхмерном пространстве, называется такой вектор 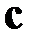, также определенный в трёхмерном пространстве, для которого выполняются следующие условия:

1. 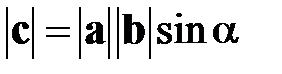, где 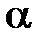– угол между векторам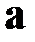и и ;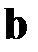

2. вектор 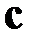ортогонален вектору 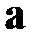и вектору ;

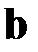3. Тройка векторов 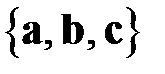– правая.

Упорядоченная тройка векторов называется правой, если видимый из конца третьего вектора кратчайший поворот от первого ко второму вектору осуществляется против часовой стрелки, в противном случае тройка называется левой.

Для получения компонент вектора, являющегося результатом векторного произведения, можно воспользоваться определителем (см. раздел 1.2), вычисляемым разложением по первой строке:

,

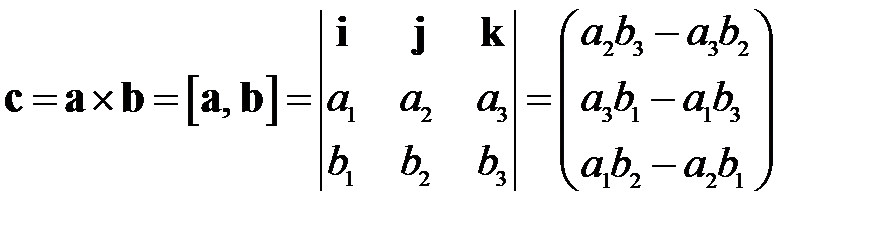где 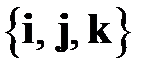– ортонормированный базис, образующий правую тройку векторов.

В случае, когда сомножители коллинеарны (лежат на одной прямой), их векторное произведение считается равным нулевому вектору. Векторное произведение обладает свойством антикоммутативности, т.е. 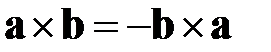, и дистрибутивности: .

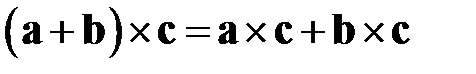С точки зрения геометрической интерпретации, модуль векторного произведения векторов равен площади параллелограмма, прилежащими сторонами которого являются эти векторы.

Смешанное произведение векторов

Смешанным (или векторно-скалярным) произведением трёх векторов 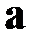, 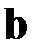и 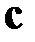, определенных в трёхмерном пространстве, называется число, равное 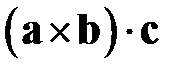и обозначаемое как .

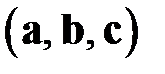Абсолютная величина смешанного произведения векторов . 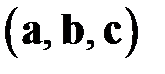. равна объёму параллелепипеда, построенного на этих векторах. При этом если тройка векторов 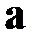, , некомпланарная (векторы не лежат в одной плоскости) и правая, то их смешанное произведение положительно, а если тройка левая – отрицательно.

Для смешанного произведения справедливы следующие равенства:

1. ;

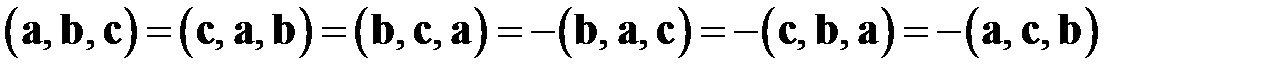2. ;

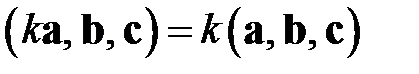3.

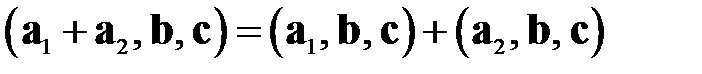
Смешанное произведение равно нулю, если среди сомножителей имеется хотя бы одна пара коллинеарных векторов.

Значение смешанного произведения можно найти, вычислив следующий определитель:

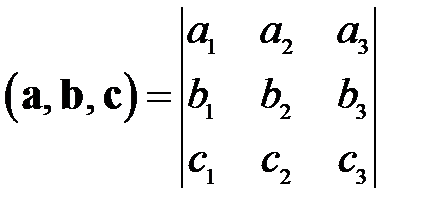
Сложение матриц

Процедура сложения матриц состоит в сложении значений их соответствующих элементов:

, , , ,

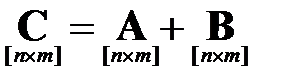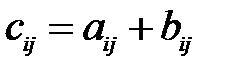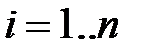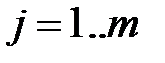где 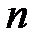– количество строк матриц 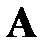, 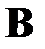и , 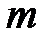– количество их столбцов, т.е. размерности слагаемых матриц должны совпадать.

Умножение матриц

Процедура умножения матриц имеет следующую формальную запись:

, , ,

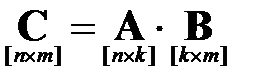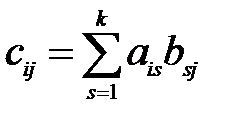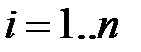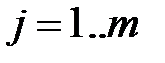
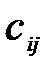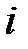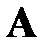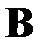Каждый элемент матрицы представляет собой результат скалярного произведения -ой строки матрицы (первого сомножителя) на -ый столбец матрицы (второго сомножителя). Таким образом, произведение двух матриц существует только тогда, когда количество столбцов первого сомножителя равно количеству строк второго сомножителя.

Умножение матриц некоммутативно, т.е. 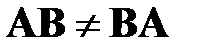, но обладает свойствами ассоциативности, т.е. 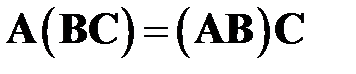, и дистрибутивности: .

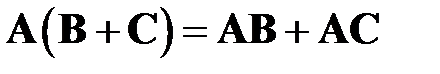Произведение двух и более матриц равно произведению соответствующих им транспонированных матриц, взятых в обратном порядке:

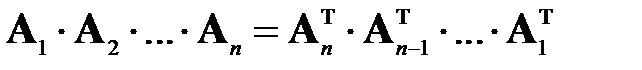
Частным случаем матричного произведения является так называемое диадное или тензорное произведение векторов:

, , ,

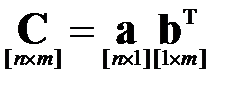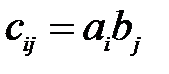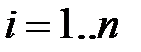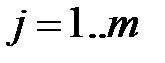
Результатом такого произведения векторов будет являться матрица, количество строк которой равно числу элементов первого сомножителя (который интерпретируется как столбец), а количество столбцов – числу элементов второго сомножителя (интерпретируется как строка). В частном случае, если размерности обоих векторов равны трём, то результатом произведения будет тензор второй валентности [8].

Умножение вектора на матрицу или матрицы на вектор также может рассматриваться как частный случай матричного произведения, причём в первом случае вектор интерпретируется как строка, а во втором – как столбец:

, ,

, ,

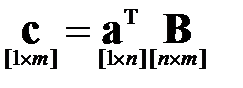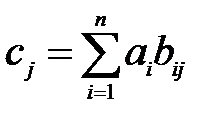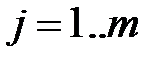
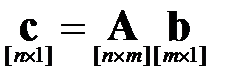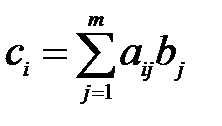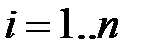
Результатом первого произведения будет являться вектор-строка, с количеством элементов, равным количеству столбцов матрицы, а второго – вектор-столбец, с количеством элементов, равным количеству строк матрицы.

Определитель матрицы

Определителем (или детерминантом) квадратной матрицы 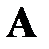размера 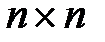называется число 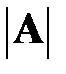, получаемое по формуле:

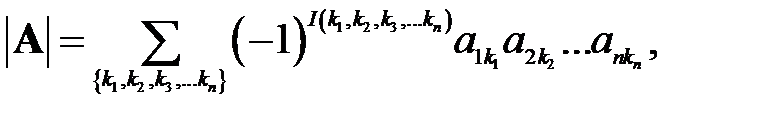
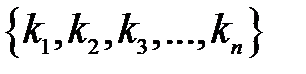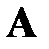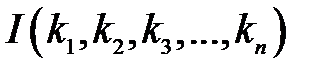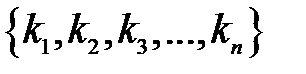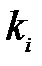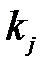где – всевозможные различные перестановки, образованные из номеров столбцов матрицы , – полное число инверсий в перестановке . Инверсией будем называть такое взаимное расположение чисел и в перестановке, при котором выполняются условия 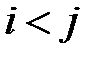и 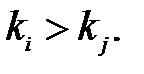Например, 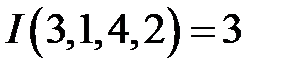. Общее число перестановок, определяющее количество слагаемых в приведенной сумме, равно .

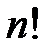Напомним основные свойства определителей, важных с точки зрения последующего рассмотрения некоторых численных методов:

1. При транспонировании матрицы ее определитель не меняется.

2. При перестановке двух столбцов или двух строк матрицы знак ее определителя меняется на противоположный.

3. Определитель матрицы, содержащей два линейно-зависимых столбца (или строки), равен нулю.

4. Определитель произведения матриц размера 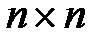равен произведению их определителей, то есть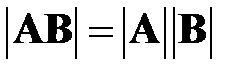

Детерминант квадратной матрицы порядка k, образованной элементами, стоящими на пересечении строк 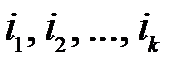и столбцов 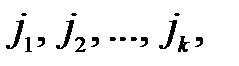называется минором k -го порядка и обозначается .

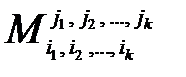Детерминант квадратной матрицы порядка 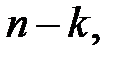образованной элементами, остающимися после вычеркивания строк 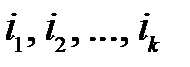и столбцов 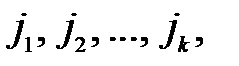называется минором, дополнительным к минору 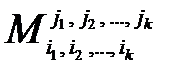, и обозначается .

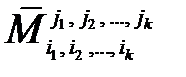Число 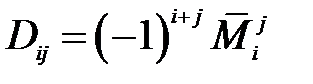называется алгебраическим дополнением элемента 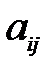матрицы 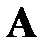, где 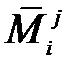– дополнительный минор элемента 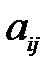. Справедливы следующие равенства:

,

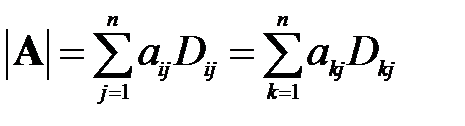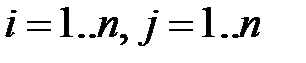
Разложение определителя по i -ой строке имеет вид:

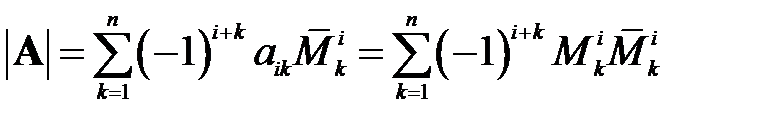
Наивысший из порядков, отличных от нуля миноров матрицы 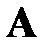, называется рангом матрицы и обозначается 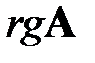. Очевидно, что если определитель матрицы не равен нулю, то её ранг равен количеству строк (столбцов), т.е. порядку матрицы.

Процедуры вычисления определителя, миноров, ранга матриц могут использоваться в анализе динамических систем, например, при проверке критерия устойчивости системы [2], условия её наблюдаемости в алгоритмах оптимальной фильтрации [3] и т.д.