Уравнение плоскости и прямой в пространстве
Поверхности второго порядка
9.1.Основные термины, формулы, положения
Различные уравнения плоскости: уравнение плоскости, заданной тремя точками; уравнение плоскости, заданной точкой и вектором нормали; общее уравнение плоскости.
Взаимное расположение двух плоскостей в пространстве; условие параллельности плоскостей; условие перпендикулярности плоскостей.
Уравнения прямой в пространстве: уравнение прямой, заданной точкой и направляющим вектором; уравнение прямой, заданной двумя точками; параметрическое уравнение прямой.
Понятие о поверхности второго порядка. Некоторые виды поверхностей второго порядка.
9.2. Типовые задания по теме
1. Используя общее уравнение плоскости, рассмотреть частные случаи расположения плоскости относительно: 1) осей координат; 2) координатных плоскостей; 3) начала координат.
2. Составить уравнение плоскости:
1) проходящей через точки А(3; -3; 0), В(-2; 0; 4), С(1; 3; 2);
2) проходящей через точку М(7; 3; 5) перпендикулярно вектору 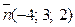 ;
;
3) проходящей через точку М(2;0;-1) параллельно плоскости 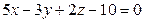 ;
;
г) проходящей через точку М (2; 5; 4) и отсекающей равные ненулевые отрезки от осей координат;
д) проходящей через точку М(1; -2; 3) и ось OZ.
3. Составить уравнение плоскости, проходящей через точку М(1; -2; 3):
1) перпендикулярно вектору 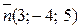 ;
;
2) параллельно плоскости 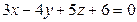 ;
;
3) проходящей через точку М (0; 2; 5) параллельно оси OY.
4. Из точки А(2; 3; -5) на координатные оси опущены перпендикуляры. Составить уравнение плоскости, проходящей через их основания.
5. Определить расстояние от точки, симметричной точке М(3; 5; 8) относительно плоскости OXY, до плоскости 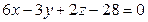 .
.
6. Составить уравнение прямой, проходящей через точку М(3; 2; -1) и пересекающую ось ОХ под прямым углом.
7. Две вершины параллелограмма АВСД заданы координатами: С(-2; 3; -5) и Д (0; 4; -7). Точка М (1; 2; -3,5) –точка пересечения диагоналей параллелограмма. Найти уравнение стороны АВ.
8. Написать каноническое и параметрическое уравнения прямой, проходящей через точку 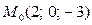 :
:
1) параллельно прямой 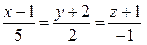 ;
;
2) перпендикулярно прямой 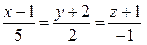 .
.
9. Даны точки А (1; 1; 1), В (2; 3; 3) и С(3; 3; 2). Составить уравнения прямой, проходящей через точку А и перпендикулярной векторам 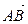 и
и 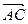 .
.
10. Даны координаты вершин пирамиды 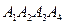 :
: 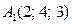 ,
, 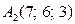 ,
, 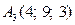 ,
, 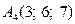 . Найти:
. Найти:
а) длину ребер 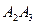 и
и 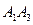 ;
;
б) уравнение прямой, содержащей сторону 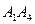 ;
;
в) уравнение плоскости и площадь грани 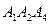 ;
;
г) объем данной пирамиды.
11. Найти длину перпендикуляра, опущенного из точки 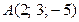 на плоскость
на плоскость 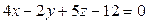 .
.
12. Найти координаты центра и радиус сферы 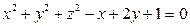 .
.
13. Составить уравнение сферы, проходящей через точки 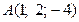 ,
, 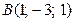 ,
, 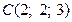 , если ее центр лежит в плоскости XOY.
, если ее центр лежит в плоскости XOY.
14. Составить уравнение сферы, если точки 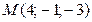 и
и 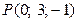 являются концами одного из ее диаметров.
являются концами одного из ее диаметров.
15. Составить уравнение окружности, образующейся в сечении сферы 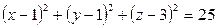 координатной плоскостью
координатной плоскостью 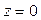 .
.
16. Найти координаты центра и радиус окружности, образующейся при пересечении сферы 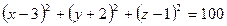 и плоскости
и плоскости 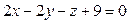 .
.
17. Используя метод сечений, построить поверхность:
1) 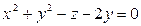 ; 2)
; 2) 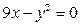 .
.
18. Установить, какие поверхности определяются уравнением:
1) 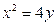 ; 2)
; 2) 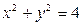 ; 3)
; 3) 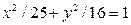 ; 4)
; 4) 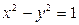 .
.
III. Примерные варианты контрольных работ
Контрольная работа №1.
№1. Дана матрица коэффициентов прямых затрат 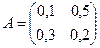 . Найти вектор совокупного продукта X для обеспечения выпуска конечной продукции
. Найти вектор совокупного продукта X для обеспечения выпуска конечной продукции 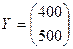 .
.
№2. Решить систему линейных уравнений по формулам Крамера:
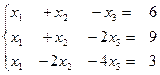 .
.
№3. Решить систему линейных уравнений в матричной форме:
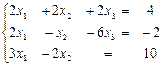 .
.
№4. Найти фундаментальный набор решений системы однородных линейных уравнений: 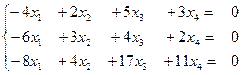 .
.
№5. Вычислить определители: а) 
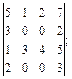 б)*
б)* 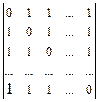 (порядок –n)
(порядок –n)
Контрольная работа №2
№1. Записать уравнения прямых, каждая из которых проходит через один из фокусов эллипса 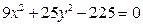 и при этом: а) параллельна прямой
и при этом: а) параллельна прямой 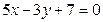 ; б) перпендикулярна прямой
; б) перпендикулярна прямой 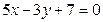 .
.
№2. Даны координаты вершин пирамиды А1А2А3А4: А1 (2; 4; 3), A2(7; 6; 3), A3(4; 9; 3), A4 (3; 6; 7). Найти: а) косинус угла между ребрами А2А3 и А1А3; б) уравнение прямой А1А4; в) уравнение плоскости, содержащей грань А1А2А4; г) высоту пирамиды, опущенную на грань А1А2А4; д) объем данной пирамиды.
№3. Найти собственные векторы и собственные значения линейного отображения, заданного матрицей 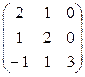 . Найти образы векторов
. Найти образы векторов 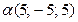 и
и 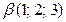 в данном отображении, если векторы заданы координатами в том же базисе, что и матрица линейного отображения.
в данном отображении, если векторы заданы координатами в том же базисе, что и матрица линейного отображения.
№4. В декартовой системе координат изобразить область допустимых решений для задачи линейного программирования. Для изготовления изделий двух видов имеется 100 кг металла. На изготовление одного изделия 1-го вида расходуется 2 кг металла, а изделия 2-го вида - 4 кг. Составить план производства, обеспечивающий получение наибольшей прибыли от продажи изделий, если отпускная стоимость одного изделия 1-го вида составляет 3 ден. ед., а изделия 2-го вида – 2 ден.ед., причем изделий 1-го вида требуется изготовить не более 40 единиц, а изделий 2-го вида – не более 20 единиц.
IV. ТЕСТОВЫЕ ЗАДАНИЯ
В тестовых заданиях выберите все верные ответы из предлагаемых вариантов.
1.Алгебраическое дополнение элемента 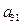 в определителе 4 порядка имеет вид:
в определителе 4 порядка имеет вид:
А) (-1)4 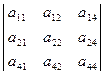 ;
;
Б) 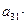 (-1)4
(-1)4 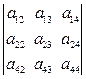 ;
;
В) (-1)4 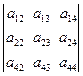 ;
;
Г) в пунктах А) - В) нет правильных ответов.
2. Определитель произвольного порядка равен 0, если:
А) строки определителя линейно зависимы;
Б) столбцы определителя линейной независимы;
В) определитель имеет пропорциональные строки;
Г) в пунктах А) - В) нет правильных ответов.
3. Из данных систем уравнений единственное решение имеется у системы…:
А) 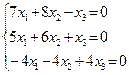 ;
;
Б) 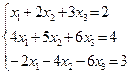 ;
;
В) 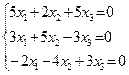 ;
;
Г) среди данных нет систем с единственным решением.
4. Пусть r - ранг совместной системы m линейных уравнений с n переменными, тогда число свободных переменных в записи общего решения системы равно:
А) m-n;
Б) r ;
В) n-r ;
Г) среди выражений А) - В) нет правильного ответа.
5. Что произойдет с рангом системы векторов, если к ней добавить нулевой вектор?
А) ранг уменьшится на 1;
Б) ранг не изменится;
В) ранг увеличится на 1;
Г) в пунктах А) - В) нет правильных ответов.
6. Система арифметических векторов (3, 1, 1, 5) и (1, 2, 3, 4) образует фундаментальный набор решений однородной системы линейных уравнений. Тогда решением данной системы является вектор:
А) (2, -1, -2, 4);
Б) (3, -4, -7, -2);
В) (4, -2, -4, 2);
Г) ни один из этих векторов не может служить решением данной системы.
7. Размерность произведения АВ для матриц А= 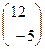 и В =
и В = 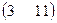 равна:
равна:
А) 2 строки, 3 столбца;
Б) 2 строки, 2 столбца;
В) 1 строка, 1 столбец;
Г) в пунктах А) - В) нет правильных ответов.
8.Пусть А – матрица совместной системы n линейных уравнений с n неизвестными, В – матрица-столбец из свободных членов данной системы, Х - матрица-столбец из неизвестных системы. Тогда верным будет равенство:
А) ВА = Х;
Б) В = АХ;
В) Х = А-1 В;
Г) в пунктах А) - В) нет правильных ответов.
9. Для арифметического пространства 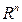 верно утверждение:
верно утверждение:
А) в 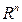 существует линейно-независимая система из (n+1)-го вектора;
существует линейно-независимая система из (n+1)-го вектора;
Б) всякий базис пространства 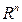 состоит из n векторов;
состоит из n векторов;
В) любая система из n векторов пространства 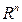 линейно независима;
линейно независима;
Г) в пунктах А) - В) нет правильных ответов.
10. Угловой коэффициент k и ордината b точки пересечения с осью OY для прямой 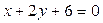 равны:
равны:
А) b = 6, k = 2;
Б) b = 3, k = 0,5;
В) b = -3, k = -0,5;
Г) в пунктах А) - В) нет правильных ответов.
11. Для прямой 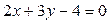 параллельной прямой является прямая…:
параллельной прямой является прямая…:
А) 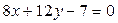 ;
;
Б) 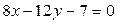 ;
;
В) 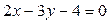 ;
;
Г) в пунктах А) - В) нет правильных ответов/
12. Уравнение с двумя переменными 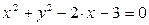 определяет на плоскости OXY…
определяет на плоскости OXY…
А) параболу;
Б) эллипс;
Г) окружность;
Д) гиперболу.
13. Расстояние от точки М(0 ;4; -1) до плоскости 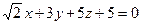 равно:
равно:
А) 2; Б) 7/2; В) 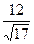 ; Г) в пунктах А) - В) нет правильных ответов.
; Г) в пунктах А) - В) нет правильных ответов.
14. Собственные значения линейного отображения с матрицей 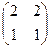 равны:
равны:
А) 1 и 2;
Б) 1, 0 и 3;
В) 0 и 3;
Г) в пунктах А) - В) нет правильных ответов .
V. Программа экзамена (зачета)
1. Матрицы. Операции над матрицами: определения и свойства.
2. Определитель n-го порядка. Разложение определителя по элементам строки (столбца). Свойства определителей.
3. Обратная матрица: определение, условия существования. Формула обратной матрицы. Единственность обратной матрицы.
4. Системы линейных уравнений (СЛУ): основные понятия. Теорема Крамера.
5. Решение СЛУ в матричной форме.
6. Равносильные СЛУ. Решение СЛУ методом Гаусса.
7. Определение, примеры, простейшие свойства векторных пространств.
8. Арифметическое n-мерное векторное пространство 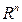 .
.
9. Линейная зависимость и независимость системы векторов. Свойства линейной зависимости.
10. Базис и ранг системы векторов. Конечномерные векторные пространства. Свойства базиса конечномерных пространств.
11. Ранг матрицы. Нахождение ранга матрицы с помощью элементарных преобразований.
12. Критерий совместности СЛУ.
13. Системы линейных однородных уравнений. Свойства решений системы однородных линейных уравнений. Фундаментальный набор решений однородной системы.
14. Матрица перехода от базиса к базису векторного пространства. Координаты вектора в различных базисах.
15. Линейные отображения векторных пространств. Матрица линейного отображения.
16. Собственные векторы и собственные значения линейного отображения.
17. Евклидовы пространства. Ортогональные системы векторов. Ортонормированные базисы.
18. Декартова прямоугольная система координат. Векторы на плоскости и в пространстве, линейные операции над ними. Модуль вектора.
19. Скалярное произведение векторов, его свойства. Векторное произведение. Смешанное произведение.
20. Различные уравнения прямой на плоскости. Взаимное расположение прямых. Типовые задачи.
21. Уравнения плоскости в пространстве. Взаимное расположение плоскостей. Типовые задачи.
22. Уравнения прямой в пространстве.
23. Кривые второго порядка. Канонические уравнения окружности, эллипса, гиперболы, параболы.
24. Линейная модель обмена. Модель Леонтьева.
VI. Задачи для подготовки к экзамену (зачету)
1. Решить систему: а) 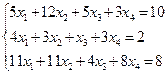 ; б)
; б) 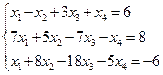 ;
;
в) 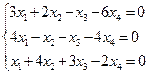 ; г)
; г) 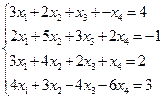 ; д)
; д) 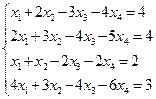 .
.
2. Даны точки 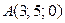 и
и 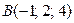 . Найти координаты и длину вектора
. Найти координаты и длину вектора 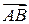 .
.
3. При каких значениях 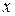 и
и 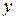 векторы
векторы 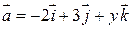 и
и 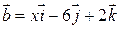 коллинеарны?
коллинеарны?
4. Даны векторы 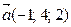 и
и 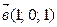 . Вычислить:
. Вычислить:
1) 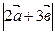 ; 2)
; 2) 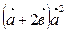 ; 3)
; 3) 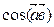 ; 4)
; 4) 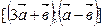 .
.
5. Даны вершины 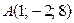 ,
, 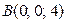 ,
, 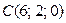 треугольника
треугольника 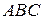 . Найти его площадь и длину высоты, опущенной из вершины
. Найти его площадь и длину высоты, опущенной из вершины 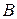 .
.
6. Компланарны ли векторы 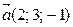 ,
, 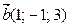 ,
, 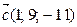 ?
?
7. Даны точки 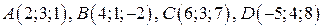 . Вычислить объем пирамиды
. Вычислить объем пирамиды 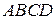 .
.
8. Составьте уравнения медиан треугольника, вершины которого находятся в точках A (2, 3), B (-3, 5) и C (7, -1).
9. Составить уравнение эллипса, если он проходит через точки М( 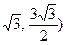 и N
и N 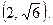
10. Даны вершины треугольника A(5,6), В(3, 4) и С(9, 1). Найдите центр описанной около него окружности.
11. Даны две смежные вершины параллелограмма А(6, 1), В(4, 3) и точка пересечения его диагоналей М(2, 3). Найдите координаты двух других его вершин.
12. Составьте уравнение прямой, проходящей через точку А(2, -1) перпендикулярно к прямой 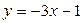 .
.
13. Найдите точки пересечения эллипса 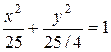 и прямой
и прямой 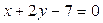 .
.
14. Исследовать взаимное расположение данных прямых. Для пересекающихся прямых найти угол между ними.
а) 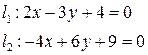 ; ; | б) 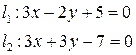 . . |
15. Найти уравнение плоскости, проходящей через точку 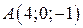 параллельно плоскости
параллельно плоскости 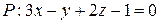 .
.
16. Написать канонические уравнения прямой, проходящей через две заданные точки 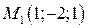 и
и 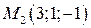 .
.
17. Написать уравнение плоскости, проходящей через три заданные точки 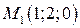 ,
, 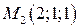 и
и 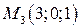 .
.
18. В базисе 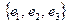
 дан вектор
дан вектор 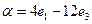 . Найти координаты этого вектора в базисе
. Найти координаты этого вектора в базисе 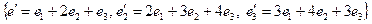 .
.
19. Найти собственные значения и собственные векторы линейного отображения 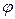 пространства L над R, заданного в некотором базисе матрицей
пространства L над R, заданного в некотором базисе матрицей 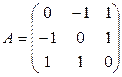 . В линейном отображении
. В линейном отображении 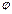 , считая, что разложение векторов дано в том же базисе, что и матрица А, найти: 1) образ
, считая, что разложение векторов дано в том же базисе, что и матрица А, найти: 1) образ 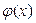 для вектора
для вектора 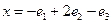 ; 2) прообраз
; 2) прообраз 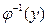 для вектора
для вектора 
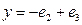
VII. Литература
Основная
1. 1. Высшая математика для экономистов [Текст] : учебник / под peд. Н. Ш. Кремер. - 3-е изд. - Москва : ЮНИТИ, 2010. – 478 с.
Дополнительная
1. Бугров, Я. С.Высшая математика [Текст]. В 3 т. Т. 1. Элементы линейной алгебры и аналитической геометрии / Я. С. Бугров, С. М. Никольский. - 8-е изд., стер. - Москва : Дрофа, 2006. - 284 с.
2. Высшая математика для экономистов [Текст] : практикум для студентов вузов, обуч. по экономич. специальностям / под peд. Н. Ш. Кремера. - 2-е изд., перераб. и доп. – Москва : ЮНИТИ-ДАНА, 2011. - 477 с.
3. Линейная алгебра. Пределы. Производная [Электронный ресурс] : задания к типовому расчету / ВятГУ, СЭФ, каф. ММЭ; cocт. Л. М. Бучина, И. Г. Лукиных. - Киров, 2010. - 39 с.
4. Письменный, Д. Т. Конспект лекций по высшей математике [Текст]. Ч. 2. Тридцать пять лекций : учеб. пособие / Д. Т. Письменный. - Москва : Айрис-Пресс. - 2008. - 256 с.
5. Сборник задач по высшей математике для экономистов [Текст] : учеб. пособие / РЭА ; под peд. В. И. Ермакова. - 2-е изд., испр. - Москва : ИНФРА-М, 2007. - 575 с.
6. Шатрова, Л. Н. Дидактические материалы по курсу высшей математики [Электронный ресурс] : учебно-метод. пособие для студентов направлений 080500.62, 230700.62, 222000 всех профилей подготовки, всех форм обучения / Л. Н. Шатрова ; ВятГУ, ФЭМ, каф. ММЭ. – Киров, 2013. - 25 с.
