Структурные характеристики статистического ряда

Наряду со степенными средними и показателями вариации для характеристики экспериментальных данных используются т. н. струк­турные характеристики. Они обычно располагаются в определенных местах вариационного ряда. Ниже будут рассмотрены некоторые структурные характеристики вариационного ряда.

Мода. Значение признака, которое наиболее часто встречается в выборке, называется модой. Если речь идет о сгруппированных дан­ных, то класс, в который попало максимальное число наблюдений, называется модальным.

Распределение, имеющее один модальный класс, называется унимодальным.Если распределение имеет два или более максимума, то такое распределение называется бимодальнымили мулътимодальнымсоответственно.

В том случае, если анализируется дискретный признак и данные сгруппированы в классы, созданные для каждого значения признака, мода непосредственно равна значению модального класса.

Если при анализе непрерывно варьирующего признака небед­ные данные сгруппированы в интервальный ряд, то мода может нахо­диться в любом месте модального интервала. Ее местоположение можно оценить, смоделировав зависимость частоты от величины ис­следуемого признака в модальном и двух соседних с ним интервалах с помощью параболы второго порядка. Такой подход позволяет полу­чить формулу для приближенной оценки моды:

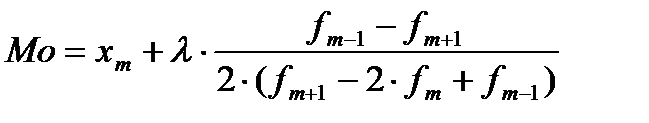
где х_т — центр модального интервала; λ— величина интервала; 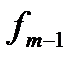— частота класса, предшествующего модальному; —частота класса, следующего за модальным; f_m - частота модального ин­тервала.

Медиана.Положение экспериментальных данных достаточно хорошо характеризуется различными степенными средними. Однако в случае малой выборки на величину этих статистик могут оказывать довольно значительное влияние крайние варианты, которые являются наименее характерными элементами выборки. Этого недостатка ли­шена медиана, значение которой определяется наиболее типичными элементами выборки. Медиана - это значение признака, которое де­лит всю выборку на две равные части. Половина вариант имеет значе­ния меньшие, чем медиана, а половина — большие.

Проще всего значение медианы определяется в случае несгруппированного набора данных. Для того чтобы определить медиану, надо предварительно упорядочить все элементы выборки по возраста­нию (ранжировать). В том случае, если число элементов в выборке нечетное, мода будет равна варианте, имеющей в ранжированном ряду порядковый номер:

, т.е. , где .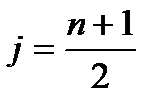

В том случае, если выборка будет иметь четное число наблюде­ний, медиана будет находиться посередине между n/2 -m и n/2 +1 -m наблюдением, т. е.:

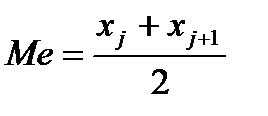, где .

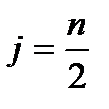В том случае, если медиану надо определить для сгруппирован­ного набора данных, начинают с того, что определяют, в каком классе она находится. Проще всего это сделать, если имеются в наличии накопленные частоты вариационного ряда. Класс, в котором находит­ся медиана (медианный класс) - это первый класс, у которого накоп­ленная частота окажется больше, чем n/2. В случае дискретной ва­риации, когда данные группировались в без интервальный вариацион­ный ряд, значение этого класса и будет медианой. Если группировка производилась в интервальный вариационный ряд, то, предполагая, что внутри медианного интервала наблюдения располагаются равно­мерно, медиану можно определить по формуле:

,

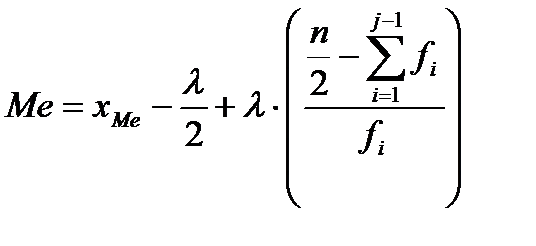где — центр медианного интервала; λ — величина интервала; n — объем выборки; j - номер медианного интервала; — накопленная частота предшествующего медианному класса; 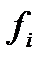— частота медианного класса.

Квантили. Медиана делит вариационный ряд на две равные час­ти. В более общем случае мы можем разделить вариационный ряд на две неравные части в любом соотношении. Статистики, которые отде­ляют от вариационного ряда определенную часть его членов, называ­ются квантилями.

Квантили, которые отделяют от вариационного ряда 1, 2, ..., 99 процентов его членов, называются перцентилями. С помощью 99 перцентилей Р₁,Р₂,...,Р₉₉ вариационный ряд делится на 100 равных час­тей. Девять статистик, которые делят вариационный ряд на десять одинаковых частей, называются децилями. Квартилями называют три квантиля (Q₁ Q₂ и Q₃), которые делят вариационный ряд на четыре равные части. Они соответствуют перцентилям, отделяющим от ран­жированного ряда наблюдений 25, 50 и 75% вариант соответственно:

, , .

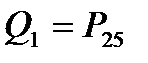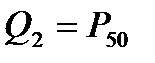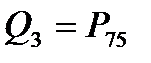Кроме того, квартиль и перцентиль, делящие вариационный ряд на две равные части, соответствуют медиане ряда наблюдений:

Q₂=P₅₀=Me.

На практике чаще всего используют перцентили Р₃, Р₁₀, Р₂₅, Р₅₀, Р₇₅, Р₉₀ и Р₉₇. Определяют квантили аналогично тому, как опре­деляют медиану. В том случае, если анализируется интервальный вариационный ряд, можно воспользоваться формулой:

,

где Р_L — квантиль, отделяющий от ранжированного ряда L процентов наблюдений; — центр интервала, в который попадает квантиль P_L ;j — номер интервала, в который попадает квантиль P_L; L — процент наблюдений в выборке, которые меньше, чем квантиль — накопленная частота интервала, предшествующего интервалу, в кото­ром находится квантиль P_L.

Чтобы определить, в каком интервале находится квантиль, следует воспользоваться накопленными частота­ми ряда распределения. Первый интервал, у которого накопленная частота окажется больше, чем величина L * n/100, и будет таким клас­сом.

Рассмотрим процесс вычисления структурных характеристик на примере вариационных рядов по диаметру и высоте. Пользуясь фор­мулами вычислим структурные характеристики для диаметров и высот:

Диаметры:

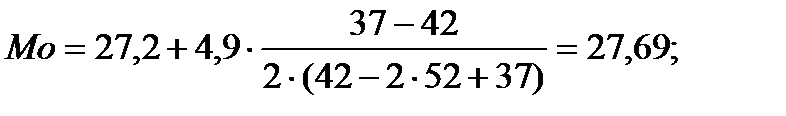
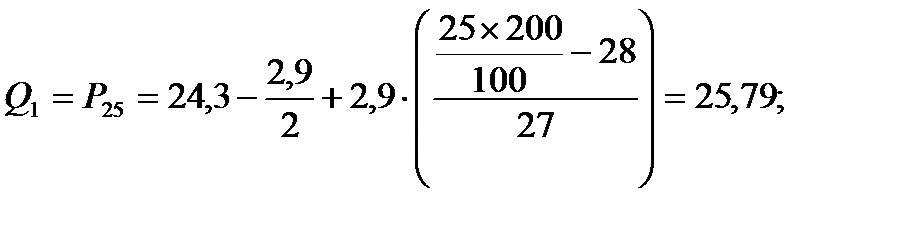
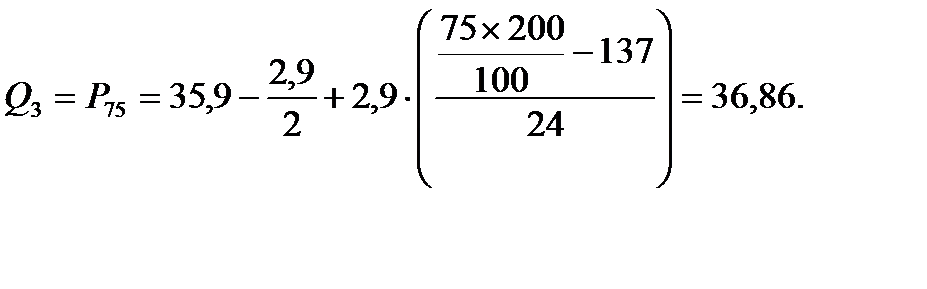
высоты