Методы на основе пошаговой одномерной оптимизации

Метод Гаусса-Зейделя (покоординатного спуска)

В основу метода Гаусса- Зейделя положены принципы более раннего метода поочередного изменения переменных. Идея последнего заключается в следующем: из начальной точки делается шаг по первой переменной, если он «удачный», то переходят к следующей переменной. Если шаг оказался «неудачным», то делается шаг в противоположном направлении. Эта процедура повторяется до тех пор, пока во всех направлениях не будут получаться одни «неудачные шаги». В этом случае величина шага уменьшается. Поиск продолжается до тех пор, пока абсолютное значение величины шага оказывается меньше заданной точности.

В методе Гаусса-Зейделя при выполнении шага по каждой переменной ищут минимум целевой функции в ее направлении, при этом значения остальных переменных остаются постоянными. Этот поиск по направлению можно производить любым известным методом одномерной оптимизации (например, методом обратного переменного шага, методом «золотого сечения» и т.п.). Таким образом, в методе Гаусса-Зейделя задача многомерной оптимизации сводится к многократному использованию метода одномерной оптимизации. Очередность варьирования переменных при этом устанавливается произвольно и обычно не меняется в процессе оптимизации [5].

Условием прекращения вычислительной процедуры при достижении заданной точности ε может служить неравенство

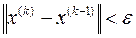
При пошаговом движении, например, в алгоритме поочередного изменения переменных поиск прекращается в точке, для которой x^(k) совпало с x^(k-1), т.е. цикл оказался нерезультативным.

Недостатком метода Гаусса-Зейделя является жесткое направление изменения каждой из составляющих решения, не зависящее от характера функции, что может привести к неоправданной остановке алгоритма в случае «овражных» функций.

Метод Хука и Дживса (метод конфигураций).

Этот метод можно рассматривать как модификацию метода Гаусса-Зейделя. Идея метода заключается в следующем: из начальной (базовой) точки выполняется одна итерация метода Гаусса-Зейделя; там, где получено уточненное значение функции, помещается временная базовая точка. После этого дальнейший поиск проводят вдоль прямой, соединяющий две базовые точки. Этот поиск проводится любым методом одномерного поиска. Найдя точку с минимальным значением целевой функции, из нее снова выполняют одну итерацию метода Гаусса-Зейделя, и дальнейший поиск снова проводят вдоль прямой, соединяющий две последние базовые точки т.д.

Недостатком метода Хука – Дживса, как и метода Гаусса- Зейделя, является его плохая сходимость при оптимизации «овражных» функций, что на стадии исследующего поиска может привести к неоправданной остановке алгоритма.

Симплексные алгоритмы.

Обычный симплекс-метод.

Симплексом в пространстве n переменных называют выпуклый многогранник, имеющий n+1 вершину. В пространстве двух переменных это треугольник, в пространстве трех переменных - тетраэдр. В обычном симплекс- методе используется правильный симплекс (все ребра которого равны). Идея симплекс-метода, заключается в следующем.

Выбирается начальный симплекс с вершинами x⁽¹⁾-х⁽²⁾-х⁽³⁾. В вершинах исходного симплекса рассчитывается значение целевой функции f(x⁽¹⁾), f(x⁽²⁾), f(x⁽³⁾). Из этих трех значений выбирается "наихудшая точка (при поиске минимума это та точка, в которой функция принимает максимальное значение). Допустим, что это точка x⁽¹⁾ . Через центр тяжести противолежащей грани x_ц.т.=(x⁽²⁾ + x⁽³⁾)/2 строится новая вершина симплекса x⁽⁴⁾, симметричная "наихудшей" вершине x⁽¹⁾ (рис.4.1):

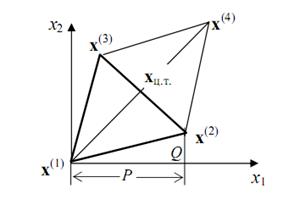
Рисунок 4.1

В результате получается новый симплекс x⁽²⁾ – x⁽³⁾ - x⁽⁴⁾ , причем значение целевой функции в двух точках x⁽²⁾ и x⁽³⁾ уже известно. Поэтому вычисляется значение функции в точке x⁽⁴⁾ и среди всех вершин ищется вершина с «наихудшим» значением. Эта вершина вновь отображается через середину противолежащей грани и вся процедура повторяется. Признаком окончания поиска является так называемая процедура зацикливания, когда вновь отображенная вершина оказывается «наихудшей». В этом случае, если заданная точность не достигается (точность обычно определяется длиной ребра симплекса), необходимо уменьшить размеры симплекса. Процедура повторяется до тех пор, пока длина ребра симплекса не станет меньше заданной точности.

В общем n–мерном случае, если обозначить отображаемую вершину симплекса за x⁽¹⁾, остальные вершины – x⁽²⁾, х⁽³⁾, …, х⁽ⁿ⁺¹⁾ отображенную вершину за x⁽ⁿ⁺²⁾, координаты центра тяжести грани, относительно которой производится отображение, определяются по формуле:

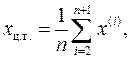
а отображаемой вершины

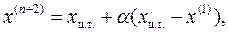
здесь множитель α > 0. При α=1 получаем зеркальное отображение х⁽¹⁾ и если исходный симплекс был правильным, то при зеркальном отображении и новый симплекс окажется правильным.

Метод Нельдера – Мида (деформируемых многогранников).

Данный метод является существенно более эффективным, чем простейший алгоритм регулярных симплексов, за счет того, что симплекс меняет свою форму от цикла к циклу. Рабочий цикл алгоритма состоит из следующих операций [5].

1. Выбирают начальный (обычно регулярный) симплекс x⁽¹⁾ -x⁽²⁾-…- x⁽ⁿ⁺¹⁾

и рассчитывают значения целевой функции в его вершинах.

2. Из найденных значений целевой функции ищут максимальное y_max = f (x_max) и минимальное значение y_min = f (x_min).

3. Отображают «наихудшую» вершину относительно центра тяжести x_ц.т. противоположной грани с коэффициентом α =1.

4. Анализируют результат отображения, сравнивая значение функции в отображенной вершине с ее значениями в вершинах предыдущего симплекса.

a) Если при этом значение функции в новой вершине оказалось меньше, чем наилучшее значение предыдущего симплекса, т.е. y⁽ⁿ⁺²⁾ < y_min , то проводят растяжение симплекса, увеличивая в β>1 (обычно β = 2) раз расстояние от отраженной вершины до центра тяжести x_ц.т.:

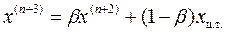(4.1)

Если после операции растяжения значение функции в новой точке уменьшается, т.е. y⁽ⁿ⁺³⁾ < y⁽ⁿ⁺²⁾, то эта вершина принимается за вершину нового симплекса. Если же увеличивается, то в качестве новой вершины берется точка, полученная после отображения y⁽ⁿ⁺²⁾.

b) Когда значение функции в отображенной вершине меньше, чем в наихудшей вершине предыдущего симплекса, но больше, чем во всех остальных, то производят операцию сжатия c коэффициентом β < 1 (обычно β = 0,5) в формуле (4.1).

c) Если значение функции в отображенной точке больше, чем в наихудшей вершине предыдущего симплекса, т.е. y⁽ⁿ⁺²⁾ > y_max , то производят редукцию (уменьшение размеров симплекса обычно в два раза), т.е. координаты всех вершин симплекса сдвигаются на половину расстояния до наилучшей точки

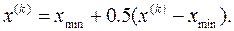
В качестве критерия остановки используют среднеквадратичную величину разности значений функции в вершинах симплекса и среднего ее значения, т.е.

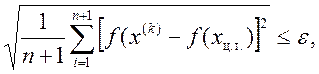
где ε - заданная точность.

Градиентные методы.

Суть всех градиентных методов заключается в использовании вектора градиента для определения направления движения к оптимуму. Вектор градиента

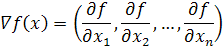
обладает несколькими свойствами, которые обуславливают его эффективное применение при поиске экстремальных значений функции многих переменных. Выделим некоторые из них.

• Вектор градиента всегда направлен в сторону наиболее быстрого возрастания функции в данной точке. Поэтому очевидно, что при поиске минимальных значений функции необходимо двигаться в противоположную сторону. Такое направление движения называют антиградиентом (-∇f(x)) или отрицательным градиентом и оно характеризует направление наиболее быстрого убывания функции.

• Градиент всегда ортогонален линии равного уровня, проходящей через данную точку x^(k).

• Согласно необходимому условию существования экстремума функции многих переменных в точке экстремума градиент функции обращается в ноль. Это свойство часто используется для проверки условия окончания поиска в градиентных методах, т.е.

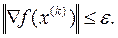
Общий алгоритм всех градиентных методов заключается в построении из некоторой начальной точки x⁽⁰⁾ последовательности приближений (рассматриваем задачу минимизации):

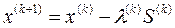(k=0, 1,…),

где S^(k) - единичный вектор в направлении градиента целевой функции f(x)

в точке x^(k):

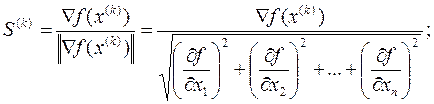
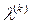– величина шага в направлении градиента.