Проверяем значимость коэффициентов.

Уровень значимости:

p=0.05;

и число степеней свободы:

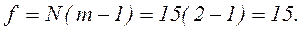
В приложении 2 находим значение соответствующее данному уровню значимости и данной степени свободы:

.

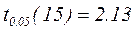Все значения 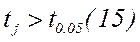являются значимыми.

Значимые: b₀, b₁, b₂, b₃, b₁₂, b₁₃, b₂₃, b₁₂₃, b₅, b₆.

Незначимые: b₄.

Определяем адекватность уравнения регрессии.

5. Из таблицы лабораторной работы № 2 выбираем столбец теоретических значений 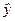. Переносим его в нашу таблицу.

Номер опыта	Экспериментальные значения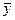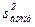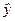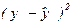
y1	y2
					69.79981191
					68.02438266
					80.84481097
					60.06938173
		70,5	70.25	0.125	70.36169304
			67.5	0.5	66.5862638
					83.4066921
					78.63126286
					77.19986079
		67,5	67.25	0.125	67.75271426
					69.1957804
			79.5	0.5	77.75545426
		66,5	66.25	0.125	66.40320533
					72.55339091
					71.41725078
Сумма столбца	-	-	-	3,375	-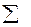

6. Для определения остаточной дисперсии заполняем последний столбец таблицы – находим квадратичную разность в каждой строке.

Номер опыта	Экспериментальные значения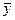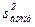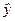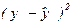
y1	y2
					69.79981191	0.040075273
					68.02438266	0.951829185
					80.84481097	0.713705577
					60.06938173	0.004813824
		70,5	70.25	0.125	70.36169304	0.130821854
			67.5	0.5	66.5862638	0.171177646
					83.4066921	1.978782671
					78.63126286	0.398492799
					77.19986079	3.240501167
		67,5	67.25	0.125	67.75271426	0.566578762
					69.1957804	1.429890763
			79.5	0.5	77.75545426	5.037985569
		66,5	66.25	0.125	66.40320533	0.162574539
					72.55339091	2.092677869
					71.41725078	2.008599766
Сумма столбцов	-	-	-	3,375	-	18.92850727

Теперь по формуле считаем остаточную дисперсию :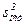

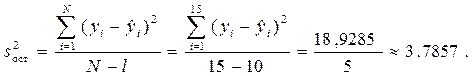
По критерию Фишера:

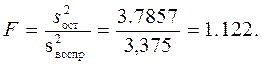
Определим табличное значение критерия Фишера:

Уровень значимости p=0.05;

число степени свободы f₁:

число степени свободы f₂:

.

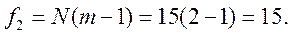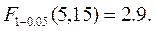
Получаем

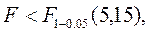
значит уравнение адекватно эксперименту.

Контрольные вопросы.

1. Для чего используют критерий Стьюдента? Приведите схему использования критерия

2. Критерий Кохрена. Формула. Принцип использования.

3. Критерий Фишера (общий случай, одинаковое число опытов).

4. Чем отличается анализ уравнения регрессии, построенного по дробному факторному эксперименту от уравнения регрессии ОЦКП?

5. Как подсчитываются степени свободы для критерия Стьюдента и критерия Фишера?

ЛАБОРАТОРНАЯ РАБОТА № 4

ОПТИМИЗАЦИЯ МЕТОДОМ КРУТОГО ВОСХОЖДЕНИЯ

БОКСА-УИЛСОНА

Цель работы.

Задача оптимизации ставится таким образом: необходимо определить экспериментально координаты экстремальной точки для заданной функции.

Основные положения.

Решение оптимизационной задачи в общем случае заключается в определении таких значений входных переменных исследуемого объекта, которым соответствует наилучшее (минимальное или максимальное) значение целевой функции. Технологические системы, как правило, являются многомерными, с большим количеством входных факторов, на значение которых к тому же накладываются дополнительные ограничения. Это требует использования методов многомерной условной оптимизации. Многие из данных методов, однако, предполагают сведение задачи к безусловной оптимизации путем преобразования целевой функции с дальнейшим применением соответствующих процедур. Поэтому изучение методов поиска экстремума функций нескольких переменных без ограничений является не менее важной задачей.

В процессе планирования эксперимента при поиске оптимума нередко требуется определить такие значения факторов, которые соответствуют максимуму или минимуму функции отклика y. На значения факторов могут накладываться ограничения, например, они должны удовлетворять условию совместимости, а их значения должны находиться в области определения Ω. Эксперименты, приводящие к достижению максимума или минимума функции отклика y, называются экстремальными или оптимизационными.

Задача оптимизации методами теории планирования эксперимента решается в два этапа [3]. На первом этапе осуществляется выход из произвольной области ω_i факторного пространства в область стационарной точки максимума или минимума, применяется полный факторный эксперимент с минимально необходимым учетом эффектов взаимодействий. На втором этапе движение к точке оптимума осуществляется видоизмененным методом градиента, который называется методом крутого восхождения.

Для наилучшего понимания сущности и особенностей методов оптимизации рассмотрим постановку задачи многомерной безусловной оптимизации, аналитический анализ целевой функции, теоретические основы часто используемых на практике численных методов – метода крутого восхождения, симплекс-метода и метода Хука и Дживса [5].

Постановка задачи.

Пусть задана функция n действительных переменных

определенная на множеств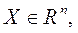е где 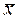- вектор-столбец, обозначающий точку в n-мерном евклидовом пространстве с координатами .

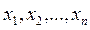Функция 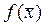имеет локальный минимум в точке 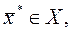если существует окрестность точки такая, что 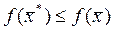во всех точках этой окрестности. В случае глобального минимума в точке для всех 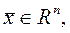справедливо неравенство .

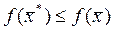Задача оптимизации - это задача максимизации или же минимизации целевой функции. Будем рассматривать задачу отыскания точек минимума функции 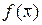, то есть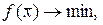 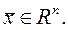Для приведения же задачи максимизации к задаче минимизации достаточно изменить знак целевой функции.