Численный метод вычисления криволинейного интеграла второго рода

Явное задание кривой интегрирования. Пусть кривая АВ (L) задана уравнением у = у (х), х [a, b], при этом абсциссы точек А и В соответственно равны a и b. Предположим, что необходимо вычислить (приближенно) величину интеграла второго рода

+ Q(x, y) dy

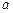
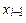
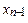
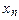
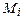
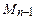
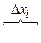
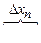
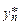
от известных функций Р(x, y) и Q(x, y)

по кривой у = у(х) от точки А до точки В.

Разобьем отрезок [a, b] на n равных

отрезков длины Δх = (рис.3). В этом

случае каждая конечная точка такого час-

тичного отрезка легко вычисляется по

формуле: x_i = а + i * Δх (i = 1, 2, … , n).

Приращения функции у = у (х) на каждом

из частичных отрезков: Δу_i = у(x_i) – у (x_{i -1}).

В точке x_i^* = (i = 1, 2, … , n) – Рис.3.

середине каждого частичного отрезка – вычислим значения функции у = у(х): у_i^* = у(x_i^*).

Замечание 1. Середина первого частичного отрезка: x₁^* = а + 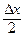. Срединные точки последующих отрезков: x_i^* = x^*_{i -1} + Δх (i = 2, 3, … , n).

Замечание 2. Значения функции у = f (х) можно вычислять не только в середине частичных отрезков, но и в других удобных для вычисления точках, например, начальных (x₁^* = а) или конечных (x₁^* = Δх) точках этих отрезков. В любом случае x_i^* = x^*_{i -1} + Δх (i = 2, 3, … , n).

Дальнейшая схема вычисления криволинейного интеграла второго рода имеет вид:

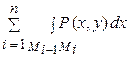+ Q(x, y) dy = + Q(x, y) dy, (7)

где

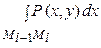+ Q(x, y) dy ≈ Р(x_i^*, у_i^*) Δх + Q(x_i^*, у_i^*) Δу_i . (8)

При параметрическом задании кривой интегрирования x = x(t), y = y(t), где

t [a, β], алгоритм приближенного вычисления криволинейного интеграла второго рода мало чем отличается от приведенного выше. Отличие лишь в том, что на равные частичные отрезки разбивается отрезок [a, β], а приращения функций Δх_i и Δу_i на i-ом частичном отрезке вычисляется по формулам

Δх_i = x(t_i) – x(t_i-1), Δу_i = у(t_i) – у(t_i-1),

где t_i – точки разбиения отрезка [a, β] (i = 1, 2, … , n).

Значения x_i^* и у_i^* в формуле (8) – это значения функций x = x(t), y = y(t) в срединной точке t_i^* i-го частичного отрезка: x_i^* = x(t_i^*), у_i^*= y(t_i^*).

Численный метод вычисления криволинейного интеграла первого рода

При явном и параметрическом задании кривой интегрированияалгоритм вычисления криволинейного интеграла первого рода практически остается таким же, как и в случае соответствующего интеграла второго рода, за исключением оператора суммирования интегральной суммы

= ,

где

≈ f (x_i^*, у_i^*) Δs_i , Δs_i = (см. рис.3). (9)

При явном задании кривой интегрирования, очевидно, что величина Δх_i постоянна (в соответствии с алгоритмом): Δх_i = Δх = (i = 1, 2, … , n).

При задании кривой интегрирования в полярных координатах разбиению подлежит угол φ = β – a на угловые интервалы длины Δφ = 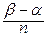. В этом случае каждая конечная точка такого частичного интервала легко вычисляется по формуле: φ_i = a + i * Δφ (i = 0, 1, 2, … , n).

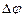
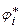
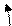
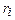
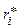
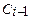
Приращения функции r = r (φ) на каждом из частичных интервалов: Δr_i = r (φ _i) – r (φ _{i -1}). В точке φ _i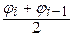^* = (i = 1, 2, … , n) – середине каждого углового частичного интервала –

вычислим значения функции r = r (φ):

r _i^* = r (φ _i^*). Тогда

= ,

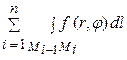где

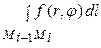≈ f (r_i^*, φ_i^*) Δs_i.

Рис.4.

Здесь Δs_i = – аппроксимация длины дуги кривой L

|М_i-1М_i| = Δl_i : r _i^* * Δφ – длина дуги C_i-1C_i окружности радиуса r _i^*, опирающейся на угол Δφ , приблизительно равная длине отрезка М_i-1N_i ; Δr_i – приращение функции r = r (φ) на i - ом частичном интервале (рис.4). Из почти прямоугольного треугольника М_i-1М_i N_i получаем выражение для Δs_i ≈ |М_i-1М_i| = Δl_i .