Формула полной вероятности и формулы Бейеса

Формула полной вероятности.Пусть пространство 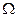некоторого вероятностного эксперимента представимо в виде объединения попарно несовместных событий , т. е.

,

для которых известны вероятности . Такие события называются гипотезами.

Рассматривается некоторое событие A, которое может появиться только вместе с одной из гипотез . Заданы условные вероятности наступления события A при осуществлении каждой из гипотез H_i: .

Тогда вероятность события А вычисляется применяя следующую теорему:

Теорема 1.5. Если событие A может произойти при появлении одной из гипотез H_i, i=1, 2, …, 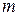, то его вероятность равна сумме произведений вероятностей каждой гипотезы и соответствующих условных вероятностей события A:

(1.14)

Д о к а з а т е л ь с т в о . Так как событие 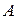может произойти с одной из гипотез , то его можно представить в виде суммы (объединения) попарно несовместных событий :

или .

Применяя аксиому 3 Колмогорова и теорему умножения вероятностей, получим утверждение теоремы:

,

где или .

Формула (1.14) называется формулой полной вероятности.

Пример 1.13.В опыте имеются три одинаковые на вид урны; в первой урне 2 белых шара и 3 черных, во второй – 4 белых шара и 1 черный, в третьей – 3 белых шара. Наугад из любой урны вынимается один шар. Найти вероятность того, что этот шар будет белым.

Решение. Эксперимент состоит в том, что наудачу извлекается шар из любой урны. Введем класс событий: событие A ={извлекается белый шар} и три гипотезы: H₁ = {выбрана первая урна}; H₂ = {выбрана вторая урна}; H₃ = ={выбрана третья урна}.

Так как урны по условию примера совершенно одинаковы, то вследствие симметрии тел, вероятности всех трех гипотез равны:

P(H₁) = P(H₂) = P(H₃) = .

Условные вероятности события ={извлечение белого шара, при условии, что выбрана тая урна}, вычислим по классической формуле:

.

Применив формулу полной вероятности (1.14), найдем вероятность события А:

P(A) = .

Ответ: вероятность события A ={извлечение белого шара} равна .

Пример 1.14. Изделия определенного вида изготавливаются тремя заводами. В магазин поступили изделия, изготовленные на трех заводах. Среди них 30% изготовлено первым заводом, 25% -- вторым и 45% -- третьим заводами соответственно. На первом заводе 97% составляют изделия высшего качества, на втором – 98% и на третьем – 99% соответственно. Определить вероятность того, что наудачу взятое изделие окажется не высшего качества.

Решение. Эксперимент, описанный в примере, состоит в выборе наудачу изделия. Построим класс событий, описывающих данный эксперимент:

событие 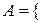взятое наудачу изделие не высшего качества ;

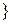события изделие произведено на том заводе ,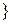

Событие 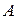может произойти с одной из гипотез Поэтому, для вычисления его вероятности применим формулу полной вероятности (1.14): .

В соответствии с условием задачи вероятности гипотез равны:

.

События изделие не высшего качества произведено -том заводе 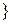, Изделия не высшего качества в продукции заводов №1, №2 и №3 соответственно составляют: 3%, 2% и 1%. Поэтому условные вероятности событий , равны: .

Применяя формулу полной вероятности, находим искомую вероятность:

0,3 0,3 + 0,25 0,2 +

+ 0,45 0,1=0,185.

Ответ: вероятность того, что наудачу взятое изделие, окажется не высшего качества, равна 0,185.

Из приведенных примеров видно, что формула полной вероятности позволяет получить ответ, минуя построение пространства элементарных событий.

Формулы Бейеса. Пусть пространство W некоторого вероятностного эксперимента представимо в виде объединения попарно непересекающихся событий , называемых гипотезами:

; , .

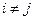Вероятности гипотез до опыта (так называемые "априорные вероятности") известны и . Условные вероятности наступления события 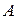при условии появления гипотез заданы.

Теперь предположим, что опыт произведен и пусть в результате реализации эксперимента наступает событие A. Тогда возникает вопрос, как изменяются вероятности гипотез при наступлении события A? Или, другими словами, спрашивается: как найти "апостериорные" вероятности гипотез , при условии, что в результате эксперимента появилось событие A?

Вероятности гипотез в этом случае вычисляются применяя следующую теорему.

Теорема 1.6. Пусть A – некоторое событие и H_i, 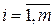, попарно несовместимые события, такие, что . Тогда, если P(A) > 0, то

(1.15)

Формулы (1.15) называются формулами Байеса.

Д о к а з а т е л ь с т в о. Если 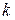фиксировано, то формула (1.15) является другой формой записи условной вероятности

,

где вероятность в числителе можно вычислить по теореме умножения: (теорема 1.2), а в знаменателе записать формулу полной вероятности (1.14). Теорема доказана.

Вероятности называют иногда апостериорными вероятностями событий H_i, 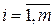, после того, как наступило событие A.

Замечание. Из доказанных теорем следует, что вероятность, приписываемая событию, изменяется тем больше, чем больше информации получено о случайном эксперименте. И, наконец, если мы имеем полную информацию, эксперимент перестает быть случайным.

Пример 1.15 . Имеется три урны; в первой урне 3 белых шара и 1 черный, во второй – 2 белых шара и 3 черных, в третьей – 3 белых шара. Наугад из одной из урн вынимается 1 шар. Этот шар оказался белым. Найти послеопытные (апостериорные) вероятности того, что шар вынут из первой, второй, третьей урны.

Решение. Эксперимент состоит в том, что наудачу извлекается шар из любой урны. Введем класс событий: событие A ={извлекается белый шар} и три гипотезы: H₁ = {выбрана первая урна}; H₂ = {выбрана вторая урна}; H₃ = ={выбрана третья урна}.

Так как урны по условию примера совершенно одинаковы, то вследствие симметрии тел, вероятности всех трех гипотез равны:

P(H₁) = P(H₂) = P(H₃) = .

Условные вероятности события ={извлечение белого шара, при условии, что выбрана тая урна}, вычислим по классической формуле:

.

Применив формулу полной вероятности (1.14), найдем вероятность события :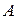

.

Применяя формулу Бейеса (1.15), находим апостериорные вероятности гипотез:

; ; .

Таким образом, вследствие информации о появлении события A, вероятности гипотез изменились – самой вероятной стала гипотеза H₃, наименее вероятной – гипотеза H₂.

Ответ: вероятности того, что шар вынут из первой, второй и третей урны соответственно равны: .

Пример 1.16. В партии изделий смешаны изделия трех изготовителей: N₁ изделий первого, N₂ изделий второго, N₃ изделий третьего. Вероятность дефекта для изделий го ( 1, 2, 3) изготовителя равна . Взято наугад одно изделие из смешанной партии, которое оказалось дефектным. Найти вероятность того, что оно изготовлено ым изготовителем.

Решение. Эксперимент состоит в выборе наугад одного изделия из смешенной партии. Введем класс событий:

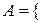взятое изделие оказалось дефектным ;

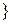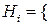изделие изготовлено тым изготовителем}, .

Априорные (до опыта) вероятности гипотез:

, ( ).

Условные вероятности события : .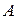

По формуле Байеса апостериорные (после опыта) вероятности гипотез равны:

, 1, 2, 3.

Тем самым определяем вероятность того, что дефектное изделие изготовлено тым изготовителем.

Ответ: вероятность того, что изделие изготовлено тым изготовителем, равна

Вопросы для самопроверки

1.Как называютсясобытия, которые представляют пространство элементарных событий?

2.Если событие 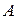может произойти с одной из гипотез , то его вероятность вычисляется по формуле?

3.Если событие 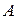может произойти с одной из гипотез , то будут ли совместными события ?

4.Если событие 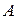может произойти с одной из гипотез , то вероятности событий , неизвестны?

5.Если событие 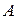может произойти с одной из гипотез , то после его появления, вероятности гипотез , не изменяются?

6.По какой формуле вычисляются вероятности гипотез , после появления события ?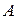

Резюме

Мы рассмотрели теоретико-множественный подход к теории вероятностей, основанный на понятиях множества элементарных событий W, множествах подмножеств , образующих s-алгебру и на котором задается неотрицательная нормированная мера - вероятность, аксиоматику Колмогорова, различные методы определения вероятностей событий, а также косвенные методы, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных.