Тема 2. Термодинамические расчеты химических равновесий
Термодинамический расчет химических реакций важен для предсказания возможности данного превращения, определения области температур и давления, при которых наиболее выгодно его проводить, и для нахождения равновесного состава продуктов. Термодинамические расчеты проводят на основании зависимостей известных из физической химии.
2.1. Константы равновесия
Равновесные соотношения при химических реакциях имеют важное значение для предсказания возможности их протекания и для выявления условий процесса, термодинамически благоприятных для его практической реализации. Они необходимы при кинетических описаниях процесса и его оптимизации.
Химические равновесия характеризуются константами равновесия.
Рассмотрим обратимую реакцию: А + Y ↔ В + Z
Константа равновесия является действительно постоянной только при выражении ее через равновесные активности:

где νi- стехиометрические коэффициенты участников реакции с соответствующим знаком; 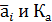 - безразмерные равновесная активность и константа равновесия.
- безразмерные равновесная активность и константа равновесия.
Для идеальных газов используют константу равновесия (КР), равную:

Для идеальных растворов ее выражают через концентрации (КС):

Иногда КС используют и для идеальных газов. Ее связь с КР выражается равенством:
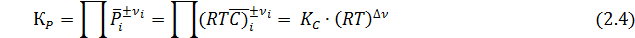
где Δν – разность суммы стехиометрических коэффициентов в правой и левой частях уравнения реакции.
Константы КР и КС не зависят от парциальных давлений или концентраций реагентов. В зависимости от стехиометрических коэффициентов они могут иметь разную размерность, а именно [давление ]Δν или [концентрация ]Δν и оказаться безразмерной при Δν =0. В технических единицах КР имеет размерность [ат Δν ]. При переходе к системе СИ первоначально рассчитывают константу КР в технических единицах, а затем пересчитывают ее в единицах системы СИ , т.е. Кр[МПа Δν] = Кр[ат Δν]·(0,1013) Δν.
Константу равновесия выражают через мольные доли:

Поскольку для идеальных газов Ni = Рi/Робщ, КN связана с КР следующим образом:
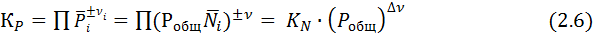
Из выражения (2.6) видно, что КN является действительной константой только при постоянном общем давлении или при Δν =0. При этом КN всегда безразмерна, совпадая по величине с КР при Δν =0 и Р = 0,098 МПа (1 ат).
Для практических расчетов равновесий удобно пользоваться величиной по форме совпадающей с константой равновесия, но выраженной через число молей вещества:

Поскольку 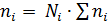 (где ∑ni – общее число молей вещества, включая инертные разбавители), то
(где ∑ni – общее число молей вещества, включая инертные разбавители), то
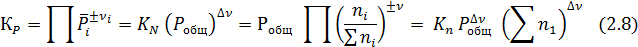
Из выражения (2.8) видно, что Кn нельзя отождествлять с константой равновесия, т.к. Кn постоянная только Δν =0 или при постоянном общем давлении и суммы числа молей веществ.
2.2. Расчет констант равновесия газофазных реакций по термодинамическим данным
Равновесные соотношения определяют двумя путями: термодинамическим путем или экспериментально. В первом случае вначале находят константу равновесия и по ней рассчитывают состав равновесных смесей, а во втором, наоборот, по составу равновесных смесей находят константу равновесия.
Для подавляющего большинства реакций, идущих при постоянном давлении, мерой их самопроизвольности является изобарно-изотермический потенциал (энергия Гиббса) ΔG, равный разности этих потенциалов для продуктов и реагентов:

Если исходные реагенты находятся в стандартном состоянии (ai =1), второй член уравнения превращается в нуль и получается известная изотерма Вант-Гоффа для идеальных газов:

где ΔG0 – стандартное изменение энергии Гиббса при химической реакции.
При равновесии ΔG (а не ΔG0) равна нулю, и знак ΔG определяет направление реакции, а именно, при ΔG<0 возможно самопроизвольное протекание реакции, ΔG>0 – невозможно.
Стандартная энергия Гиббса связана с энтальпией и энтропией реакции известным уравнением:

Константу равновесия для идеальных газов Ка находят из уравнения (2.10), иногда ее выражают как функцию температуры:

Для приближенного расчета константы равновесия предполагают, что энтропия ΔН0 и энтальпия ΔS0не зависят от температуры и используют термодинамические таблицы, имеющиеся в монографиях и справочниках.
В справочниках приводятся данные о стандартной энергии Гиббса, энтальпии образования соединений из простых веществ и абсолютной энтропии для стандартного состояния вещества при 298°К. Первые две величины обозначаются и ΔG0f,298, ΔН0f,298, а последняя - S0298 .
Если соединения при указанных условиях (1 ат и 298 °К) является жидким или твердым, эти данные соответствуют его фиктивному состоянию в виде идеального газа. В свою очередь 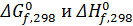 относятся к образованию соединения из простых веществ (О2, Н2,С и др.) в их обычном для 0,1 МПа и 298 К газообразном, жидком или твердом состоянии в виде наиболее стабильной модификации. Стандартную энергию Гиббса можно рассчитать различными способами, известными из курса физической химии.
относятся к образованию соединения из простых веществ (О2, Н2,С и др.) в их обычном для 0,1 МПа и 298 К газообразном, жидком или твердом состоянии в виде наиболее стабильной модификации. Стандартную энергию Гиббса можно рассчитать различными способами, известными из курса физической химии.
Если известны ΔG0f,298 при образовании веществ, то их изменения при какой-либо химической реакции можно рассчитать по правилу Гесса, т.е. вычитанием из суммы ΔG0f,298 продуктов реакции такой же суммы для исходных веществ по формуле:

Пример 1. Рассчитать константу равновесия для реакции

Известно, что для С ΔG0f,298= 0 Дж/моль; СО2 ΔG0f,298= -394572 Дж/моль, а для СО ΔG0f,298= -137334 Дж/моль.
Решение.
Изменение энергии Гиббса составит
ΔG0298 = -2·137334 –(0-394572) = 119903 Дж/моль.
lnKp,298 = ‒ ΔG0298/RT = ‒ 48,4
Константа равновесия Kp,298=9,5·10 -22.
Чаще константу равновесия определяют по энтальпиям и энтропиям образования веществ. Изменение соответствующих характеристик при химической реакции нетрудно вычислить как сумму для продуктов и исходных реагентов с учетом величины и знака стехиометрических коэффициентов:
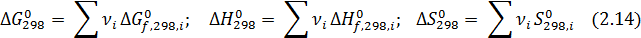
Если в реакции участвуют простые вещества, то для них ΔН0 и ΔG0 при всех температурах приняты равными нулю, но надо учитывать их абсолютную энтропию.
Пример 2. Рассчитать константу равновесия при 1000 К для реакции

Решение.
По справочнику [1] находим
| Вещество | ΔН0, кДж/моль | S0, Дж/(моль·К) |
| СО2 | -393,7 | 213,74 |
| СО | -110,58 | 197,66 |
| С (графит) | 5,4 |
Из этих данных вычисляем:
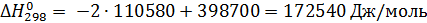
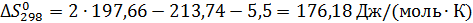
Отсюда при 1000 К энергия Гиббса равна:
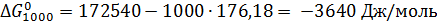
Теперь по уравнению (2.12) рассчитываем при R = 8,31441 Дж/(моль·К).
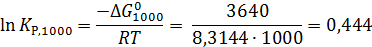
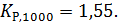
2.3. Расчет констант равновесия с учетом влияния температуры
Для более точного расчета констант равновесия химических реакций необходимо учитывать, что в действительности термодинамические функции определенным образом зависят от температуры, что нужно учитывать при точном расчете.
Для энергии Гиббса температурная зависимость выражается формулой:
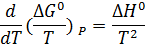
Практическое применение этого уравнения осложняется тем, что стандартное изменение энтальпии реакции также зависит от температуры в соответствии с законом Кирхгоффа:

где 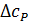 - разность изобарных теплоемкостей продуктов и исходных веществ, которую рассчитывают с учетом стехиометрии реакции:
- разность изобарных теплоемкостей продуктов и исходных веществ, которую рассчитывают с учетом стехиометрии реакции:

В соответствии с уравнением (2.16) и дифференциальным выражение 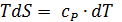
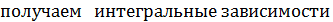 стандартной энтальпии и энтропии реакции от температуры:
стандартной энтальпии и энтропии реакции от температуры:
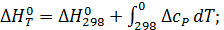
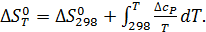
Таким образом, точное уравнение для энергии Гиббса:
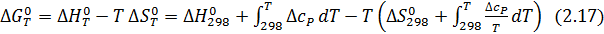
Одно из приближенных его решений, предложенное Темкиным и Шварцманом, основано на применении регрессионного уравнения зависимости теплоемкости веществ от температуры:

Коэффициенты уравнения определяются экспериментально, причем обычно бывает достаточно первых трех членов уравнения. Значение коэффициентов для разных веществ приводится в справочниках.
Используя уравнения (2.15, 2.16, 2.17), получаем:
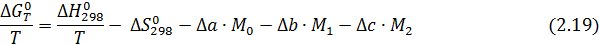
где Δа, Δb, Δс – суммы коэффициентов уравнений теплоемкости для реагентов и продуктов, полученные в соответствии с уравнениями (2.16, 2.17); М0,М1, М2 - интегралы Темкина-Шварцмана, вычисляемые по формулам
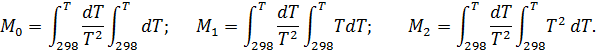
Интегралы Темкина-Шварцмана, включающие под знаком второго радикала температуру в соответствующей степени, зависят только от температуры. Они заранее рассчитаны с интервалом в 50 и 100 градусов, а внутри расчетных интервалов следует находить интерполяцией.
Пример 3. Рассчитать константу равновесия реакции дегидрирования этанола в ацетальдегид в газовой фазе при 473°К :

Решение
Из справочных данных [1] находим
| Вещество | 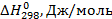 | 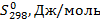 | а | b·103 | с·106 |
| С2Н5ОН | -235466 | 282,2 | 14,98 | 208,7 | 71,14 |
| СН3-СНО | -166467 | 265,9 | 31,07 | 121,5 | -36,60 |
| Н2 | 130,7 | 29,09 | -0,837 | 2,013 |
Отсюда для реакции имеем:
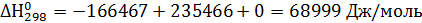
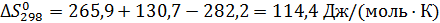
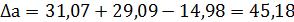
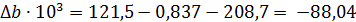
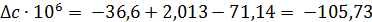
Интегралы Темкина-Шварцмана при 473°К равны:
М0= 0,0919; М1= 0,0324·103 М2= 0,0115·106
Тогда энергия Гиббса по формуле (2.19) равна
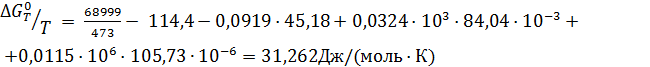
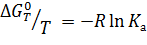 , то
, то 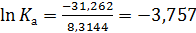 ,
,
Ка = 0,0233 ат = 2,33·10-3 МПа.
2.4. Расчет констант равновесия в системах реальных газов
Все изложенные выше методы расчета термодинамических потенциалов и констант равновесия пригодны лишь для газов, близких к идеальным, т. е. находящихся при низких давлениях и достаточно удаленных от состояния насыщенного пара. Между тем многие реакции органического синтеза проводятся при высоких давлениях, когда поведение реального газа существенно отклоняется от идеального. Для таких реакций используют выражения констант равновесия через активности (2.1, 2.10). Для сохранения общий вид термодинамических зависимостей вместо парциальных давлений используют так называемые летучести, или фугитивности газов f, при постоянной температуре удовлетворяющие условию:

При практических расчетах удобнее пользоваться активностью а, которая в общем случае представляет собой отношение летучести вещества в данном состоянии к его летучести f0 в стандартном состоянии:

Стандартная летучесть f0 принята равной летучести газа в идеальном состоянии при давлении 1 ат или 0,1013мМПа. Для газов за стандартное принято состояние идеального газа при давлении 0,1 МПа (1 ат), поэтому для идеального газа активность равна его парциальному давлению, а для реального газа — его летучести. При повышенном давлении они могут существенно различаться, что учитывается коэффициентом летучести γ, равным отношению летучести вещества к его парциальному давлению в газовой фазе:

При давлении Р =1 ат реальный газ можно принять за идеальный ( f0= 1 ат), тогда:

Коэффициент летучести находят по принципу соответственных состояний, согласно которому значение γ для реальных газов является одинаковыми, если газы находятся при тех же приведенных температурах (τ) и давлениях (π):

При определении приведенного давления (π) берут не парциальное, а общее давление, т.к. газ испытывает влияние всех компонентов смеси, а для водорода вместо критических параметров используют Ркр +8 ат и Ткр + 8К. Все это позволяет использовать для нахождения γ любых реальных газов одни и те же таблицы.
Изотерму Вант-Гоффа для реальных газов можно представить в следующей форме
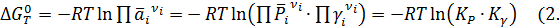 25)
25)
Таким образом, введение понятия летучести позволяет свести учет неидеальности газов к вычислению некоторой величины Кγ, зависящей от стехиометрии реакции и коэффициентов летучести реагентов.
Пример 4. Рассчитать константу равновесия Кр реакции синтеза метанола в газовой фазе при 300 °С и 30 МПа:

если известно, что при этой температуре ΔG0573 = 39767 Дж/моль, а критические параметры веществ следующие:
Ткр, К Ркр, МПа
Окись углерода 134,1 3,5
Водород 32,2 1,28
Метанол 513,0 7,87
Решение
Используя эти величины, рассчитаем для всех реагентов приведенные параметры и находим коэффициент летучести γ:
Вещество τ π γ
Окись углерода 4,27 8,57 1,14
Водород 4,25 14,40 1,11
Метанол 1,12 3,81 0,38
Отсюда
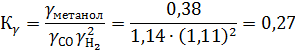
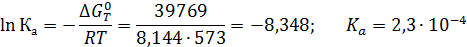
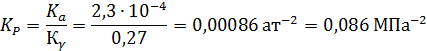
Поскольку при Р ≈ 0,1 МПа КР = Ка, очевидно, что в этом случае с повышением давления до 30 МПа КРувеличивается в 3,7 раза (1/0,27).
2.5. Приближенные методы расчета термохимических характеристик химических соединений
Для расчета термодинамических характеристик химических реакций по способам, изложенным в предыдущем разделе, нужно знать ряд величин, определяемых экспериментально; теплоемкость веществ и ее зависимость от температуры, тепловой эффект и т.п. В некоторых случаях одно или несколько необходимых исходных данных в литературе отсутствует. В этом случае приходится прибегать к менее точным методам расчета ΔG° и Кр, не требующим, однако, постановки эксперимента, а основанным лишь на данных о структуре молекул реагирующих веществ и ее изменении в ходе реакции.
Наибольшее распространение при практических расчетах находит так называемый метод структурных групп, который позволяет приближенно рассчитывать стандартные теплоты, энтропии образования и коэффициенты в уравнении температурной зависимости теплоемкости для широкого круга органических веществ.
Для органических веществ многих типов (углеводородов разных классов, кислородсодержащих соединений, галогенпроизводных, аминов, сернистых соединений и др.) стандартные теплоты образования ΔН0298, энтропии образования S0298 и коэффициенты а, b и с в уравнении теплоемкости могут быть подсчитаны по правилу аддитивности, учитывая число атомов углерода в молекуле, характер связей и тип функциональных групп. Исходными данными для таких расчетов служат термодинамические функции девяти «основных» веществ, представленных в табл. 2.1 Выбор этих соединений основан на том, что они являются первыми членами некоторых наиболее часто встречающихся гомологических рядов: парафинов, циклопарафинов, ароматических углеводородов, аминов, эфиров и т. п.
Таблица 2.1. Термодинамические функции основных веществ
| Вещество | ΔН0 f,298, кДж/моль | S0298, Дж/(моль·К) | Коэффициенты уравнения Δс0р=Δа+ΔbТ+ΔсТ2, Дж/(моль·К) | ||
| Δа | Δb·103 | Δс·106 | |||
| Метан | -74,9 | 186,3 | 15,9 | 69,6 | -13,56 |
| Циклогексан | -123,22 | 298,4 | -48,3 | 584,7 | -103,5 |
| Бензол | 82,98 | 269,4 | -17,6 | 382,3 | -217,8 |
| Нафталин | 148,21 | 337,9 | 13,2 | -145,7 | |
| Метиламин | -29,73 | 241,6 | 16,8 | 128,6 | -36,4 |
| Диметиламин | -32,66 | 16,4 | 202,2 | -59 | |
| Триметиламин | -45,64 | 288,9 | 16,5 | 275,7 | -81,6 |
| Диметиловый эфир | -192,59 | 265,4 | 26,9 | 266,7 | -47,9 |
| Формамид | -207,25 | 249,1 | 27,3 | 105,4 | -31,3 |
Молекула соединения, для которого проводится расчет, должна быть построена исходя из соответствующего «основного» вещества, причем в первую очередь постепенным замещением атомов водорода метальными группами строится углеродный скелет. Введение в молекулу функциональных групп (если оно необходимо) проводится путем замены не водорода, а заранее введенной метальной группы. При этом функциональная группа замещает столько метальных групп, какова кратность ее связи с атомом углерода, например для введения - одной карбонильной группы нужно заместить сразу две метальные группы. Это обстоятельство нужно учитывать при построении углеродного скелета молекулы.
В ходе построения углеродного скелета молекулы вещества, для которого производится расчет, каждое замещение водорода метильной группой, как и введение функциональной группы, приводит к изменению величин ΔН0298, S0298 и коэффициенты а, b и с на некоторые поправки. Величина поправки зависит от типа замещения и природы функциональной группы. Первое замещение водорода в молекуле «основного» вещества называется первичным; таким же является расширение кольца в молекуле циклопентана (табл. 2.2). Для бензола и нафталина все последовательные замещения в ядре – первичные, однако поправки зависят от относительного расположения заместителей. Все остальные замещения водорода называются вторичными; для них величина поправки зависит от структуры молекулы, в которой проводится замещение (табл. 2.3).
Таблица 2.2. Поправки на первичное замещение атомов водорода группами -СН3
| «Основная» группа | ΔН0 f,298, кДж/моль | S0298, Дж/(моль·К) | Коэффициенты уравнения Δс0р=Δа+ΔbТ+ΔсТ2, Дж/(моль·К) | ||
| Δа | Δb·103 | Δс·106 | |||
| Метан | -10,47 | 43,33 | -8,37 | 97,1 | -38,2 |
| Циклогексан | |||||
| - поправка на расширение кольца на 1 атом С | -45,93 | 5,36 | -10,51 | 127,2 | -49,4 |
| - первое замещение | -32,95 | 45,13 | 8,92 | 78,1 | -23,9 |
| Бензол | |||||
| - первое замещение | -32,93 | 50,58 | 3,27 | 69,8 | -22,7 |
| - второе замещение | |||||
| -- 1,2- | -31,02 | 33,03 | 17,88 | 40,7 | -7,8 |
| -- 1,3- | -32,78 | 37,97 | 3,22 | 73,1 | -25,9 |
| -- 1,4- | -32,07 | 32,7 | 7,37 | 56,3 | -14,3 |
| Нафталин (первое замещение) | -18,84 | 50,24 | 1,51 | 72,1 | -24,6 |
| Метиламин | -23,86 | -0,42 | 73,4 | -22,4 | |
| Диметиламин | -26,38 | -0,42 | 73,4 | -22,4 | |
| Триметиламин | -17,17 | -0,42 | 73,4 | -22,4 |
Структурные особенности молекулы определяются ее строением, причем учитывается тип атома, у которого происходит замещение (тип А) и тип соседнего, наиболее замещенного атома углерода (тип В). Типы А и В обозначаются цифрами от 1 до 4, соответствующие степени замещения данного атома – первичного, вторичного, третичного и четвертичного.
| Степень замещения атома углерода | Первичный ‒СН3 | Вторичный =СН2 | Третичный ≡СН | Четвертичный =С= |
| Тип атома |
Тип атома, находящегося в ароматическом кольце, обозначают цифрой 5. В соответствии с этим, например, поправки к энтропии при переходе от пропана к изобутану (А=2, В=1) и от этилбензола к изопропилбензолу (А = 2, В = 5) неодинаковы и составляют соответственно —26,42 и —25,87 кДж/моль.
Таблица 2.3.Поправки на вторичного замещение атомов водорода группами -СН3
| Типовые числа | ΔН0 f,298, кДж/моль | S0298, Дж/(моль·К) | Коэффициенты уравнения Δс0р=Δа+ΔbТ+ΔсТ2, Дж/(моль·К) | |||
| А | В | Δа | Δb·103 | Δс·106 | ||
| -19,89 | 42,29 | 2,05 | 92,3 | -37,5 | ||
| -20,6 | 38,43 | 4,56 | 74,5 | -27,1 | ||
| -18,51 | 40,7 | -4,19 | 88,2 | -33,6 | ||
| -20,93 | 46,05 | 5,82 | 71,7 | -24,6 | ||
| -19,59 | 4,56 | 78,3 | -3*0 | |||
| -26,42 | 23,32 | -1,26 | -36,7 |
Продолжение табл. 2.3.
| Типовые числа | ΔН0 f,298, кДж/моль | S0298, Дж/(моль·К) | Коэффициенты уравнения Δс0р=Δа+ΔbТ+ΔсТ2, Дж/(моль·К) | |||
| А | В | Δа | Δb·103 | Δс·106 | ||
| -26,5 | 29,93 | -2,68 | 97,9 | -41,7 | ||
| -21,98 | 27,34 | 3,35 | 80,7 | -32,2 | ||
| -16,04 | 31,23 | 10,55 | 67,4 | -24,6 | ||
| -25,87 | 28,14 | 1,55 | 86,6 | -32,3 | ||
| -34,42 | 11,76 | -1,17 | 101,4 | -43,9 | ||
| -29,31 | 16,2 | -3,89 | 103,5 | -37,5 | ||
| -21,73 | 16,71 | -13,7 | 129,6 | -58,9 | ||
| 20,68 | 7,87 | -0,59 | 115,4 | -43 | ||
| -38,52 | 5,44 | 1,76 | 67,8 | -19,6 | ||
| Замена водорода в сложных или простых эфирах | -29,3 | 58,6 | -0,04 | 73,6 | -22,3 | |
| Замена водорода в кислоте с образованием сложного эфира | -39,8 | 69,9 | 1,84 | 69,6 | -20,7 |
Наличие в молекуле искомого вещества кратных связей тоже учитывают при расчете путем введения соответствующих поправок; в этом случае поправки определяются типами А и В двух атомов, между которыми возникает кратная связь (табл. 2.4). На этом этапе расчета учитывают и появление сопряженных связей, вносящее свой вклад в изменение термодинамических характеристик. Например, при превращении изобутанав изобутен (А=1, В = 3) поправка к теплоте образования равна118 кДж/моль, а при переходе (того же типа) от изопропилбензола к α-метилстиролу кроме этой проявляется еще поправка на сопряжение с ароматическим кольцом, равная – 8,37 кДж/моль.
Таблица 2.4. Поправки на замещение одинарных связей кратными (сложными) связями
| Тип кратной связи | ΔН0 f,298, кДж/моль | S0298, Дж/(моль·К) | Коэффициенты уравнения Δс0р=Δа+ΔbТ+ΔсТ2, Дж/(моль·К) | ||
| Δа | Δb·103 | Δс·106 | |||
| 1=1 | 137,66 | -10,05 | 0,88 | -34,7 | 5,7 |
| 1=2 | 125,6 | -0,88 | 4,69 | -47,7 | 13,9 |
| 1=3 | 118,19 | -0,46 | 9,13 | -65,4 | 26,9 |
| 2=2 (цис) | 118,86 | -4,98 | -14,95 | 0,6 | 4,5 |
| 2=2 (транс) | 114,72 | -9,04 | 5,32 | -53,5 | 16,2 |
| 2=3 | 111,87 | -1,17 | -8,46 | -43,5 | |
| 3=3 | 107,6 | -2,76 | -1,72 | -63,4 | 26,8 |
| 1≡1 | 312,24 | -41,24 | 19,76 | -102 | -26,3 |
| 2≡2 | 274,24 | -16,62 | 4,19 | -107,6 | -39,8 |
| 1≡2 | 291,07 | -17,94 | 19,23 | -110,4 | 36,9 |
| Дополнительные по правки для вводимых двойных связей | |||||
| - сопряженных | 55,1 | -15,66 | 9,38 | 4,9 | -1 |
| - чередующихся | -17,92 | -21,44 | -3,94 | 16,2 | -14,6 |
| - смежных с ароматическими кольцами | -8,37 | -11,1 | 4,23 | -13,6 | 5,5 |
Последним этапом расчета является учет поправок при замещении метильных групп на соответствующие функциональные группы (табл. 2.5).
Таблица 2.5. Поправки на группы, замещающие группы –СН3
| Замещающая группа | ΔН0 f,298, кДж/моль | S0298, Дж/(моль·К) | Коэффициенты уравнения Δс0р=Δа+ΔbТ+ΔсТ2, Дж/(моль·К) | ||
| Δа | Δb·103 | Δс·106 | |||
| -ОН | -136,91 | 10,89 | 13,27 | -62,2 | 23,4 |
| -ОН (Ar-орто) | -199,71 | ||||
| -NO2 | 5,02 | 8,37 | 26,38 | -81,8 | 44,5 |
| -C≡N | 163,28 | 16,74 | 15,24 | -58,3 | |
| -Cl | |||||
| - для первого атома Cl у С | 9,17 | -78,9 | 26,2 | ||
| - для каждого последующего атома Cl | 18,84 | ||||
| - F | -146,54 | -4,19 | 9,38 | -98,9 | 49,5 |
| = О (альдегид) | -54,01 | -51,5 | 15,11 | -233,3 | 95,1 |
| = О (кетон) | -55,27 | -10,05 | 21,02 | -276,1 | 126,6 |
| - СООН | -364,25 | 64,48 | 35,59 | -63,1 | 33,2 |
| - SH | 66,15 | 21,77 | 17,04 | -104,5 | 51,8 |
| - C6H5 | 135,23 | 90,85 | -3,31 | 224,5 | -80,4 |
| - NH2 | 51,5 | -20,1 | 5,28 | -30,6 | 9,3 |
Окончательный результат расчета – термодинамические характеристики вещества – находят, суммируя соответствующие свойства исходного «основного» вещества и все поправки, появившиеся при построении углеродного скелета молекулы, введении функциональных групп и кратных связей.
Пример 5. Найти термодинамические характеристики ацетона, исходя из структурной формулы
Решение.
Структурная формула ацетона I требует первоначального построения молекулы вида II, исходным веществом для которой является метан.

Решение представлено в табл. 2.6.
Таблица 2.6. Расчет термодинамических характеристик ацетона
| Замещающая группа | ΔН0 f,298, кДж/моль | S0298, Дж/(моль·К) | Коэффициенты уравнения Δс0р=Δа+ΔbТ+ΔсТ2, Дж/(моль·К) | ||
| Δа | Δb·103 | Δс·106 | |||
| 1. Метан | -74,9 | 186,3 | 15,9 | 69,6 | -13,56 |
| 2. Первичное замещение Н на -СН3 | -10,47 | 43,33 | -8,37 | 97,1 | -38,2 |
| 3. Вторичное замещение Н на -СН3 (тип А=1, В=1) | -19,89 | 42,29 | 2,05 | 92,3 | -37,5 |
| 4. Вторичное замещение Н на -СН3 (тип А=2, В=1) | -26,42 | 23,22 | -1,26 | 91,0 | -36,7 |
| 5. Вторичное замещение Н на -СН3 (тип А=3, В=1) | -34,42 | 11,76 | -1,17 | 101,4 | -43,9 |
| 6. Замена двух групп -СН3 на =О (кетон) | -55,27 | -10,05 | 21,02 | -267,7 | 126,5 |
| ИТОГО | -221,37 | 296,85 | 28,17 | 183,7 | -43,36 |
| Справочные данные | -216,83 | 296,09 | 22,49 | 201,9 | -63,56 |
2.6. Расчет состава равновесных смесей простых реакций
Дальнейшая задача при расчете равновесий состоит в нахождении по найденным или вычисленным константам равновесия и заданным начальным условиям (Рi,0, Сi,0) состава равновесных смесей и равновесных степеней конверсии. Рассмотрим вначале случай простых реакций.
Если, в соответствии со стехиометрическим уравнением реакции, общее число молей веществ и объем реакционной смеси не изменяются, при расчете равновесия газофазных реакций проще всего заменить равновесные парциальные давления веществ их начальными давлениями и равновесными степенями конверсии. При избытке одного из реагентов можно воспользоваться введенным ранее мольным соотношением β (1.12).
Пример6.Найти состав равновесной смеси иравновесную степень конверсии для газофазной реакции

если КР = 15 и реакция проводится при 2-кратном мольном избытке спирта по отношению к кислоте и общем давлении 0,12 МПа.
Решение.
Согласно уравнениям (1.9, 1.11, 1.13) при равновесии имеем:
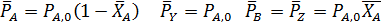
Тогда:
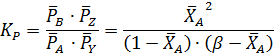
Откуда получаем квадратное уравнение:
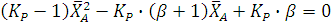
Его решение дает:
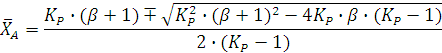
Один из корней ( 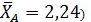 является недействительным, т.к. степень конверсии не может быть больше единицы. Другой корень дает равновесную степень конверсии (
является недействительным, т.к. степень конверсии не может быть больше единицы. Другой корень дает равновесную степень конверсии ( 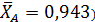
В соответствии с этим парциальные давления компонентов в равновесной смеси будут равны
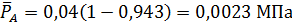
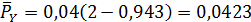 МПа
МПа
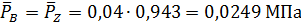
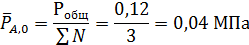
Из решения этого примера вытекает, что для реакций, не сопровождающихся изменением общего числа молей веществ, равновесная степень конверсии зависит не от давлений (концентраций), а только от мольного соотношения реагентов: с его увеличением равновесная степень конверсии ключевого реагента повышается. Так, для предыдущей задачи, если бы исходные вещества находились в эквимолярных количествах (β = 1), равновесная степень конверсии составила бы только 0,795. Это влияние избытка одного из реагентов (обычно более дешевого) широко применяется в промышленности и является общим для всех реакций между двумя или более реагентами, в том числе и для таких, где общее число молей изменяется.
Объем реакционных смесей обычно является постоянным для любых жидкофазных реакций, что позволяет использовать тот же метод расчета, но с заменой давления на концентрации или мольные доли.
Пример 7. Найти состав равновесной смеси для жидкофазной реакции

если константа равновесия равна КС =4, реакция проводится без посторонних растворителей при 4-х кратном мольном избытке бензола (Y) по отношению к диэтилбензолу (А). Плотность всех компонентов можно принять одинаковой и равной 870 г/л. Объем исходной смеси равен 1 л.
Решение
Начальная концентрация диэтилбензола – СА,0, а равновесная - 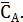
Равновесные концентрации бензола и этилбензола составят
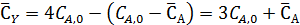
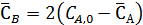
Из выражения для константы равновесия имеем:
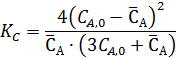
Неизвестную СА,0 находим из условия, что объем исходной смеси, соответствующей начальным концентрациям, равен 1 л.
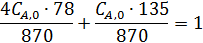
где 78 и 135 – молекулярные массы бензола и диэтилбензола.
Следовательно, CA,0= 1,965 моль/л, что дает
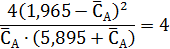
Отсюда получаем (моль/л):
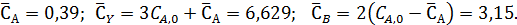
При изменении объема реакционной смеси во время реакции расчет равновесных смесей можно осуществить способом парциальных молярных балансов, составляемых на 1 моль основного реагента А.
Пример 8. Реакции гидрирования бензола в циклогексан

протекает без посторонних разбавителей при общем давлении Робщ и мольном соотношении водорода к бензолу, равном βY. Вывести общее уравнение для равновесных парциальных давлений всех веществ и для степени конверсии бензола ХА, если константа равновесия равна КР. Рассчитать равновесную степень конверсии бензола при βY=3 и βY=10, Робщ=0,1 МПа и Робщ= 1,0 МПа, если КР= 13800 МПа-3.
Решение.
Составим парциальный молярный баланс реакции и находим Рi
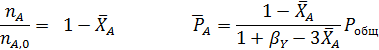
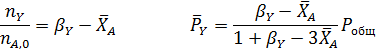
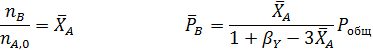
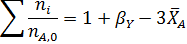
Отсюда получаем уравнение для расчета 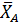 :
:
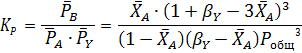
Это уравнение четвертой степени решается способами вычислительной математики (например, в программе Mathcad). Из всех его корней только один удовлетворяет условию 0< 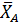 < 1. При заданных значениях Робщ и βY получаем значения ХА, представленные в табл. 2.7.
< 1. При заданных значениях Робщ и βY получаем значения ХА, представленные в табл. 2.7.
Таблица 2.7. Значение равновесной степени конверсии реагента А при заданных значениях Робщ и βY
| Робщ , МПа | βY | 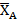 |
| 0,1 | 0,318 | |
| 0,1 | 0,906 | |
| 1,0 | 0,85 | |
| 1,0 | 0,999 |
Из данных, приведенных в табл. 2.7, видно, что для реакций, сопровождающихся уменьшением объема, на смещение равновесия вправо положительно влияет не только избыток второго реагента, но и увеличение общего давления.
Пример 9. Для реакции дегидрирования этилбензола в стирол

вывести общее уравнение зависимости ХА от общего давления Робщ и коэффициента разбавления этилбензола водяным паром β0 = РН2О/РА,0. Рассчитать ХА при Робщ=0,1 МПа, β0=3 и βY=10, а также Робщ=0,1 и 0,01 МПа в отсутствии разбавителя, если КР= 0,15 МПа.
Решение.
С
