Тема 1. Характеристика химических процессов

1.1. Классификация химических реакций

Химические процессы органической технологии характеризуются протеканием большого числа химических реакций с участием промежуточных активных частиц, которые существенным образом влияют на скорость и направление превращения исходных веществ. Вследствие огромного разнообразия химических реакций их, как правило, классифицируют по общим признакам. Применительно к реакциям промышленного органического синтеза в основу могут быть положены следующие признаки.

А. Фазовое состояние реагентов и продуктов реакции.

Если компоненты реакционной системы находятся в пределах одной фазы (газ, жидкость, твердая фаза), реакцию называют гомофазной. При существовании двух или более фаз (газ – жидкость, газ‒ жидкость ‒твердая фаза и др.) реакцию называют гетерофазной.

По зоне протекания химического процесса реакции делятся на гомогенные и гетерогенные.Гомогенные реакции протекают в объеме какой-либо одной фазы, гетерогенные - на поверхности раздела фаз, например, реагент - гетерогенный катализатор.

Этерификация уксусной кислоты этанолом в жидкой фазе в присутствии серной кислоты относится к гомогенным гомофазным реакциям, а в присутствии твердого катализатора к гетерогенным гомофазным каталитическим реакциям.

Процессы окисления органических соединений в жидкой фазе молекулярным кислородом относятся к гомогенным гетерофазным реакциям, т.к. взаимодействие органического субстрата происходит с растворенным кислородом. Аналогичным образом протекает сульфирование ароматических углеводородов, когда реагенты находятся в двух несмешивающихся фазах, а реакция протекает в объеме одной из фаз (кислотной фазе).

Б. Природа воздействия физического агента на реакционную систему.

При воздействии теплоты и радиации на реакционную систему происходит активация реагентов за счет теплового движения молекул и протекает термическая реакция. При этом реакция протекает изотермически, если в течение всего процесса температура постоянна, и неизотермически, если температура меняется в ходе реакции, при отсутствии теплоотвода реакция протекает адиабатечески.

В экзотермических реакциях происходит выделение теплоты (Δ Н < 0), в эндотермических - поглощение теплоты (Δ Н > 0). В термонейтральных реакциях энтальпия реакции равна нулю (Δ Н =0).

При воздействии света и радиации (α, β, γ – излучения) протекают фотохимические реакции и радиационно-химические реакции.

При пропускании электрического тока через реакционную систему в объеме системы или на поверхности электродов протекают электрохимические реакции.

Механохимические реакции протекают в твердом теле или при его механическом разрушении.

В. Катализ и ингибирование реакций

При введении в реакционную систему катализатора, ускоряющего химический процесс, происходит так называемая каталитическая химическая реакция. Катализатор многократно вступает в промежуточные химические реакции и регенерируется к моменту образования конечного продукта. Если катализатор образуется в процессе химической реакции, то такая реакция называется автокаталитической.

Введение в реакционную систему соединения, которое тормозит или останавливает химическую реакции, называется ингибированием химического процесса, а введенное вещество – ингибитором.

Г. Стехиометрии и механизм химических реакций

С точки зрения стехиометрии все химические реакции подразделяются на простые и сложные.

Простые (однозначные) реакции характеризуются тем, что при их протекает единственное необратимое превращение и не образуется иных стабильных продуктов, кроме записанных в уравнении реакции:

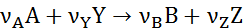
Простые реакции могут быть элементарными и неэлементарными. Элементарные реакции протекают при непосредственном взаимодействии исходных веществ, т.е. при этом отсутствуют какие-либо микростадии, через которые идет реакции. Неэлементарные реакции имеют ряд химических микростадий, в которых участвуют промежуточные комплексы или частицы, не фигурирующие в стехиометрическом уравнении, например,

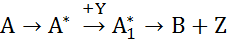
Каждая их промежуточных стадий, составляющих неэлементарную реакцию является элементарной.

Совокупность связанных друг с другом элементарных реакций, из которых состоит неэлементарная реакция, составляет механизм реакции, точнее, кинетический механизм реакции.

Стехиометрически сложные (многозначные) реакции – реакции, которые записываются в виде двух или более стехиометрического уравнения.

Сложные реакции состоят из простых по стехиометрии реакций. К ним относятся:

а) Обратимые реакции:

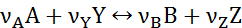
б) Параллельные реакции

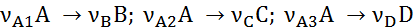
в) Последовательные реакции:

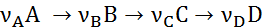
Д. Тип реакции (направление протекания реакции)

Простые реакции могут протекать по следующим направлениям:

а) Реакции присоединения (символ Ad), например:

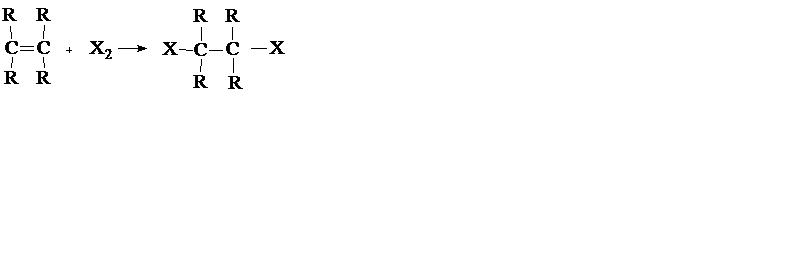
б) Реакции элиминирования (отщепления) (символ Е), например:

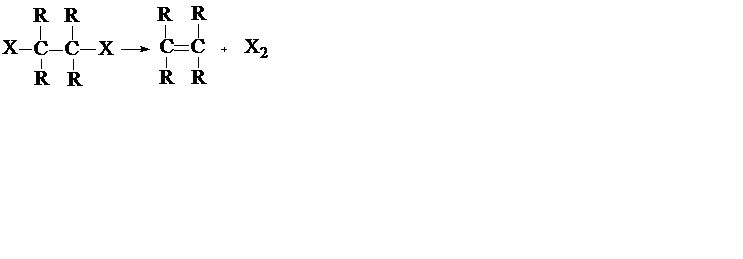
в) Реакции замещения (символ S), например:

г) Реакции изомеризации (перегруппировки), например:

Е. Характер изменения связи(тип механизма реакции)

а) Гомолитические (радикальные) реакции

Если в процессе реакции происходит разрушение или образование двухвалентной связи с участием частиц с неспаренными электронами ‒ радикалов, то такие реакции называют гомолитическими или радикальными.

Радикальные реакции обозначаются индексом R и могут протекать по различным направлениям (типам).

Например:

б) Гетеролитические (ионные) реакции

Если в процессе реакции расщепление связи происходит с переходом электронной пары к одному из партнеров связи, а образование связи – с обобществлением электронной пары одного из реагентов, то такая реакция называется гетеролитической или ионной.

В гетеролитических реакциях химические превращения происходят с участием ионов (катионов и анионов) и могут относиться либо к нуклеофильным реакциям (индекс N), либо электрофильными реакциями (индекс Е).

Реакция является нуклеофильной, если атакующий реагент выполняет функцию нуклеофила (донора электронной пары). Реакция относится к электрофильной, если атакующий реагент – электрофил (акцептор электронной пары).

Нуклеофильные реагенты: отрицательные ионы, соединения с неподеленными парами электронов, соединения с этиленовыми двойными связями и ароматические вещества.

Электрофильные реагенты: положительные ионы, кислоты Льюиса, ацетилены, соединения с карбонильными группами,галогены.

Нуклеофильные и электрофильные реакции (по типу реакции) могут протекать как реакции присоединения, замещения или изомеризации.

Нуклеофильное и электрофильные присоединение, например:

Нуклеофильное и электрофильное замещение, например

Нуклеофильная и электрофильная изомеризация (перегруппировка), например:

Ж. Число частиц, принимающих участие в элементарных реакциях или в лимитирующей стадии неэлементарных реакций

- Мономолекулярные реакции, например:

- Бимолекулярные реакции

- Тримолекулярные реакции

Согласно буквенным символам в обозначении реакции указывается направление (тип) реакции, тип реагента (механизм) и молекулярность. Первой обозначается направление реакции, затем – тип реагента и далее цифрой – молекулярность. Например: S_N1, S_N2, Ad_N 2, S_Е2, Ad_Е 2, Е1, Е2 и т.д.

1.2. Материальные расчеты для химических реакций

Первичной основой учения о химических превращениях веществ является стехиометрия, на которой базируются все количественные соотношения при химических реакциях.

В технике количества веществ чаще всего выражают через их массу m_i, измеренную в г, кг или т. Однако при химических реакциях вещества расходуются и образуются в мольных соотношениях, поэтому для материальных расчетов более удобно их мольные количества n_i, выраженные в моль или кмоль. Они связаны с массой соотношением

где М_i молекулярная масса вещества.

Соотношение (1.1) позволяет после расчета количества вещества в молях перейти к расчетам в кг.

Мольные количества n_i используют для характеристики периодических процессов. В непрерывных процессах, когда вещества подаются и выходят из реактора непрерывно, более приемлемой материальной характеристикой является мольный поток, который для стационарного режима выражается уравнением:

где F_i – мольный поток, моль/время или кмоль/время; t – время, за которое подают или выводят из реактора n_i молей вещества.

Для каждой простой реакции, которая записывается уравнением

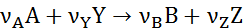
можно написать следующее равенство, являющееся основным соотношением баланса реакции:

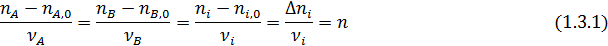
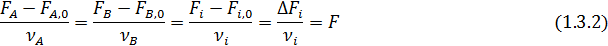
где n_i и n_i,0, F_i и F_i,0 ‒ мольные количества или мольные потоки веществ соответственно в любой момент реакции и в исходной смеси.

Эти равенства справедливы при условии, что стехиометрические коэффициенты расходуемых веществ берутся со знаком минус, а образующихся – со знаком плюс. При этом величина n (или F) всегда положительна, инвариантна в отношении участников реакции называется полнотой реакции. Из равенства (1.3) вытекает уравнение материального баланса простой реакции

Зная начальные и конечные мольные количества (n_i,0, n_i) или мольные потоки (F_i,0, F_i) для одного вещества, вычисляют значения полноты реакции (n или F) по формулам (1.3.1- 1.3.2), а затем по формулам (1.4.1 -1. 4.2) рассчитывают мольные количества или мольные потоки для всех других веществ, участвующих в реакции.

Из уравнений (1.3) следует, что мольное соотношение образующихся или расходуемых веществ при простых реакциях равно соотношению стехиометрических коэффициен­тов этих веществ в уравнении реакции:

Пример 1. Полагая, что реакция диспропорционирования циклогексена с образованием бензола и циклогексана

является простой, вычислить мольное количествопродуктов реакции, если известно, что n_A,0 =12 кмоль, n_B,0 = n_Z,0 =0; n_A= 3 кмоль.

По уравнению (1.3.1) находим полноту реакции n:

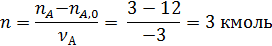
Тогда по уравнения (1.4.1) имеем:

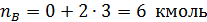
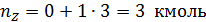
Материальный баланс представлен в табл. 1.1.

Таблица 1.1. Материальный баланс диспропорционирования циклогексена

Вещество	Концентрация	Молекулярный вес	Количество вещества	Объем V, м3
кмоль	кг
ЗАГРУЖЕНО
С6Н10
ИТОГО
ПОЛУЧЕНО
С6Н10
С6Н12
С6Н6
ИТОГО

Для материального расчета сложных реакций для каждой из независимых реакций по ана­логии с выражением (1.3) можно записать уравнения полноты реакции

где индекс i соответствует веществу, а индекс j ‒ реакции.

Тогда, имея в виду, что каждое из веществ может участвовать в нескольких реакциях 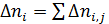получим

Пример 2. При дегидратации этанола протекают реакции

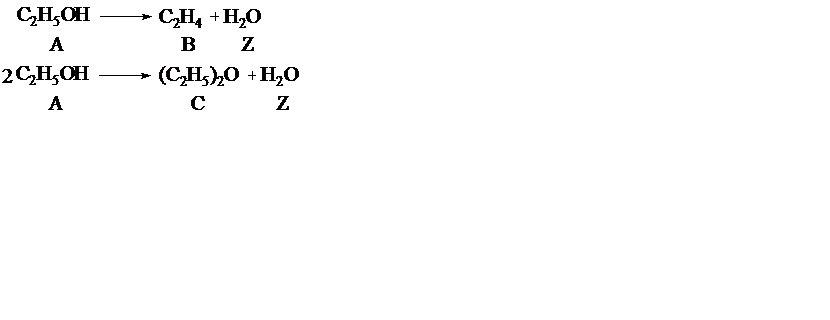
Рассчитать материальный баланс процесса, если F_A,0 = 1000 кмоль/ч, F_B = 300 кмоль/ч, F_C = 200 кмоль/ч.

Решение.

По уравнению (1.7)

F_B = 0 + 1∙F₁ F₁= 300

F_C= 0 + 1∙ F₂ F₂ = 200

Тогда

F_A = 1000 - 1∙300 - 2∙200 = 300 кмоль/ч

F_Z = 0+ 1∙300 + 1∙200 = 500 кмоль/ч

На основании данного расчета составлена таблица материального баланса(табл. 1.2).

Таблица 1.2. Материальный баланс процесса дегидратации этанола

Вещество	Мол. вес	Количество вещества
кмоль/ч	кг/ч
Загружено
Этанол
ИТОГО
Получено
Этанол
Этилен
Диэтиловый эфир
Вода
ИТОГО

1.3. Безразмерные количественные характеристики химических процессов

Кроме мольных количеств и потоков в химии и технологии большое значение имеют безразмерные характеристики матери­ального баланса - степень конверсии, селективность и выход.

Степень конверсии реагента А - доля прореагировавшего исходного реагента А относительно его начального количества:

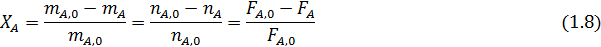
В таком написании степень конверсии может меняться от 0 до 1, но ее нередко выражают в процентах, умножая правые части предыдущих выражений на 100. При этом обычно степень кон­версии определяют по основному исходному реагенту А, но ее можно аналогично записать и для других реагентов, например для реагента Y:

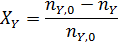В предыдущем примере дегидратации этанола степень его конверсии составляет:

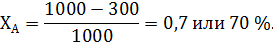
Из уравнения (1.8) следует

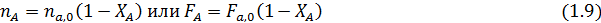
Дли простых и обратимых реакций, когда имеются единст­венное независимое превращение, степень конверсии — вполне достаточная характеристика мате­риального баланса.

Из уравнения (1.8) можно вывести зависимости n_i (F_i) от n_А,0 (F_А,0) и степени конверсии основного реагента Х_А:

Если реагент Y взят в избытке , т.е.

В этом случае степень превращении, найденная по реагенту А, связана с количеством второго реагента F_Y следующим соотношением:

Для сложных реакций степень конверсии показывает лишь долю превращенного реагента, но не дает представления о направлениях его превращения, которое определяется селективностью и выходом.

Селективность представляет собой количественную оценку эффективности целевой реакции по сравнению с побочными реакциями. Различают полную (интегральную) селективность и дифференциальную селективность.

Интегральная селективность – это доля (или процент) превращенного исходного реагента А, израсходованная на образование данного продукта В в соответствии со стехиометрией:

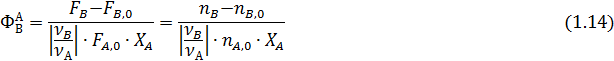
Сумма интегральной селективности для всех полученных веществ равна единице.

В примере 2 дегидратации этанола получают

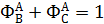
Дифференциальная селективность – отношение скорости накопления целевого продукта В к скорости расходования реагента А в соответствии со стехиометрией реакции:

Интегральная и дифференциальная селективности связаны между собой соотношением:

Выход продукта – отношение реально полученного количества продукта к максимально возможному его количеству, которое могло быть получено при данных условиях осуществления химической реакции. Следовательно, выражение для расчета выхода можно получить из уравнения (1.14) при Х_А=1

Из формул (1.14) и (1.18) вытекает, что выход равен произведению селективности на степень конверсии:

При этом сумма выходов ключевых веществ по основному реа­генту А с учетом уравнения (1.14) равна степени конверсии это­го реагента:

Рассчитаем выходы и проверим полученные соотношения для примера 2 дегидратации этанола:

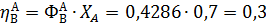
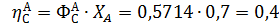
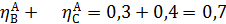
Из уравнений (1.14 и 1.18) мольные количества или потоки продуктов можно выразить через их селективность и выходы:

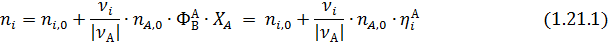
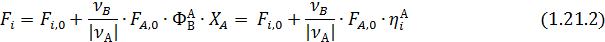
При расчете материальныхбалансов процесса все или часть исходных данных (за исключением n_i,0 или F_i,0)может быть задана безразмерными характеристиками — степенью конверсии, селективностью или выходом. Тогда, используя выведенные уравнения, рассчитывают мольные количества или потоки всех веществ и составляют таблицу материального баланса.

1.4. Материальные расчеты сложных реакций

При анализе системы сложных реакции необходимо определить число стехиометрически независи­мых превращений, уравнения которых нельзя получить комби­нацией уравнений других реакций (сложением, вычитанием, ум­ножением стехиометрических коэффициентов на постоянные множители). В большинстве случаев это легко сделать последо­вательным исключением стехиометрически зависимых реакций. Так, при обратимом превращении уравнение обратной реакции легко получить, умножив на минус единицу уравнение прямой реакции; следовательно, в этом случае имеется только одно не­зависимое превращение.

В системе сложных реакций дегидрата­ции этанола

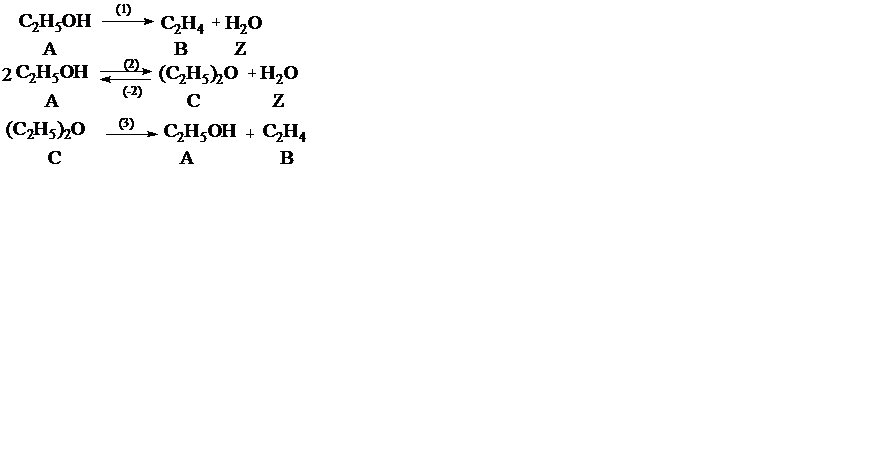
исключив реакцию (‒2), как обратную реакции (2), и реакцию (3), уравнение которой можно получить вычитанием уравнения (2) из уравнения (1), находим, что система имеет лишь две независи­мые реакции.

В более сложных случаях для определения числа (R) сте­хиометрически независимых превращений используют методы матричной алгебры, составляя стехиометрическую матрицу, строки и столбцы которой соответствуют определенным веществам и реакциям. Ранг стехиометрической матрицы равен числу независимых реакций.

Пример 3. При окислении этилена протекают реакции

Составить материальный баланс для реакций окисления этилена, если начальный мольный поток этилена F_A,₀ = 150 кмоль/час; Х_А = 0,4; Ф_В^А= 0,7; β_Y = 0,6.

Решение.

Стехиометрическая матрица процесса окисления этилена представлена в табл. 1.3.

Таблица 1.3. Стехиометрическая матрица процесса окисления этилена

С2Н4	О2	С2Н4О	СО2	Н2О
-1	-0,5				а
-1	-3				b
	-2,5	-1			c
-1	-0,5				a
	-2,5	-1			d=b-a
	-2,5	-1			c
-1	-0,5				a
	-2,5	-1			d=b-a
					e=c-d

Определяя ранг приведенной матрицы, находят R = 2.

В качестве независимых реакций выбирают реакции 1 и 2, т.к. реакцию 3 можно получить вычитанием из реакции 2 реакцию 1.Затем по известным формулам рассчитывают материальный баланс и на основе этого расчета составляют таблицу материального баланса.

По формуле (1.9) рассчитывают количество непрореагировавшего этилена (А):

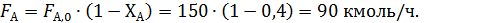
Из формулы (1.19.2) при условии, что F_В,0=0 кмоль/ч, находят количество образовавшегося оксида этилена:

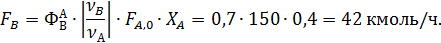
Из формулы (1.15) находят селективность образования оксида углерода и воды:

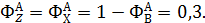
Отсюда количество образовавшихся оксида углерод и воды равны

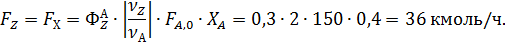
Для определения остаточного количества кислорода находим полноту реакций 1 и 2 по уравнению (1.6)

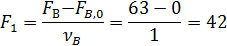
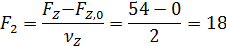
Начальный мольный поток кислорода определяем из формулы (1.12):

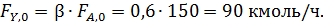
По формуле (1.7.2) рассчитываем остаточное количество кислорода:

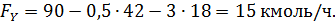
Материальный баланс процесса окисления этилена представлен в табл. 1.4.

Таблица 1.4. Материальный баланс процесса окисления этилена

Вещество	Мол. вес	Количество
кмоль/ч	кг/ч
Загружено
Этилен
Кислород
ИТОГО
Получено
Этилен
Кислород
Окись этилена
Оксид углерода
Вода
ИТОГО

1.5. Концентрации, парциальные давления и мольные доли

Кроме мольных количеств или потоков веществ и безразмер­ных характеристик баланса, важное значение имеют концентра­ции, парциальные давления и мольные доли, на которых осно­ваны расчеты термодинамики и кинетики реакций, а также хи­мических реакторов.

Концентрация соответственно для периодических и непре­рывных процессов определяется как отношение мольного коли­чества (мольного потока) вещества к объему V (л или м³) или кобъемному потоку W (л/час или м³/час), в котором равномерно распределено данное веще­ство:

При этом объем и объемный поток для газофазных реакций необходимо принести к давлению и температуре в реакторе, учитывая объем всех компонентов системы, в том числе разбавителей.

Если объем или объемный поток остаются постоянными во времени реакции, то в ранее выведенных формулах для расчета материального баланса и для расчета безразмерных характеристик реакций вместо n_i (Fi) можно подставлять С_i. Это типично для жидкофазных процессов, а для газофазных встречается в тех случаях, когда реакция протекает при постоянном общем давлении и температуре без изменения числа молей веществ или без промежуточного разбавления смеси.

Для идеальных газов их концентрации пропорциональны парциальным давлениям (P_i = C_iRT), и, следовательно, те же уравнения подходят и для парциальных давлений веществ. При этом последние являются более удобной характеристикой со­стояния газа, так как при постоянном общем давлении они, в отличие от концентраций, не зависят от температуры.

Более сложные соотношения существуют для реакций, про­текающих с изменением объема. При жидкофазных процессах это бывает при поглощении какого-либо газа жидкостью или при разложении жидкого вещества с образованием летучих продуктов. Тогда объем жидкой фазы в любой момент реакции находят с помощью коэффициента изменения объема ε по урав­нению

где V₀ и V — начальный и текущий объемы, a z— некоторая функция, от которой зависит изменение объема (например, сте­пень конверсии или число присоединившихся молей газа). При этом коэффициентизменения объема определяется выражением

и является положительным при увеличении объема смеси вовремя реакции и отрицательным при его уменьшении. Тогда текущаяконцентрация вещества равна:

Пример 4. При оксиэтилировании спиртов для получения неионогенных ПАВ барботируют газообразный этиленоксид через жидкую реакционную массупри катализе гидроксидом натрия:

Найти концентрацию NaOH, когда к 1 моль спирта присоединилось 10 моль, этиленоксида, если начальная концентрация NaOH равна С₀=0,022 моль/л, а коэффициент изменения объема при поглощении одной оксиэтильной груп­пы равен ε =0,12.

Решение.

По уравнению (1.25) находим:

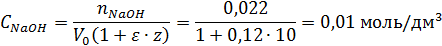
Для газофазных процессов изменение объема обычно про­исходит из-за неравенства числа молей веществ во время реак­ции (разложение, присоединение и др.). Его можно учитывать с помощью введенных выше коэффициентов изменения объема, которые для газообразного состояния веществ зависит от начального и конечного числа молей смеси:

Например, для реакций

а) А→ В + Z в отсутствии разбавителей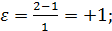

б) А + Y→ В при эквимолярном соотношении реагентов и в отсутствии разбавителей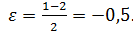

Для реакции (а) при мольном соотношении инертным разбавителем равным β₀ получим

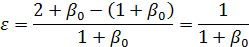
Для реакции (б) при мольном избытке второго реагента β_Y имеем:

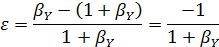
Особенно удобно использовать коэффициенты изменения объема для простых реакций, когда имеем

При подстановке F_i как функцию F_А,0 и Х_А оказывается, что С_i выражается через начальную концентрацию ( ).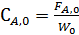

Например, для реакции А→ В + Z имеем:

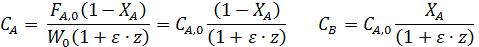
Последние уравнения справедливы Т=const. Из-за пропорциональности концентраций парциальным давлениям можно записать соотношения, не зависящие от температуры:

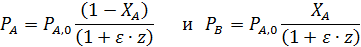
Более общий способ расчета парциальных давлений состоит в использовании мольных долей веществ, которые находят из парциальных молярных балансов

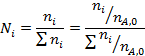
После этого парциальные давления веществ вычисляют по формуле

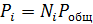
где Р_общ — общее давление смеси, которое для большинства процессов можно считать постоянным.

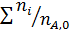
Пример 5.При совмещенном дегидрохлорировании и хлорировании 1,1,2,2-тетрахлорэтана протекают такие суммарные реакции:

Вывести уравнениядля парциальных давлений веществ с учетом содержания инертных примесей и мольного соотношения реагентов β_Y. Рассчитать эти давления при β_Y=0,55, η_В=0,45, η_С = 0,54, содержании в хлор-газе 7% инерт­ных примесей и общем давлении 0,12 МПа.

Решение

Имеем уравнения парциального молярного баланса:

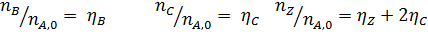
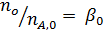
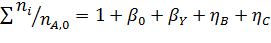
При содержании в хлор-газе 7% инертных примесей имеем:

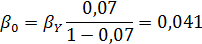
Отсюда получаем:

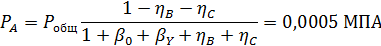
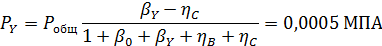
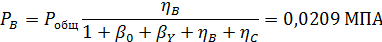
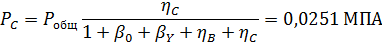
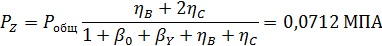
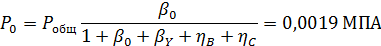
Вопросы для самопроверки

1. Расскажите на примерах о химическом процессе, его стехиометрии и механизме реакции.

2. Напишите уравнение материального баланса для стехиометрически простых и сложных реакций.

3. Напишите уравнения степени конверсии реагента А, интегральной и дифференциальной селективности и выхода продукта И.

4. Напишите уравнения, связывающие между собой степень конверсии, селективность и выход.

5. Напишите уравнения расчета количества реагентов А и Y, а также продуктов реакции В и Z через степень конверсии реагента А.

6. По каким признакам можно классифицировать реакции в органической технологии? Покажите на примерах.

7. В каких случаях применяется коэффициент изменения объема. Напишите формулу для его расчета. Приведите примеры.

Контрольные задачи

Приведены в Сборнике задач по курсу «Теория химико-технологических процессов органического синтеза» - Инженерные расчеты в химической технологии (работа 1).