Блок-схема алгоритм расчета новой точки методом Эйлера

Блок-схема алгоритма решения ОДУ 1-го порядка методом Эйлера

8.2. Модифицированный метод Эйлера (метод Рунге– Кутта 2-го порядка)

Пусть требуется найти решение задачи Коши:

, , .

Как и в методе Эйлера, на отрезке 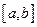зададим конечное множество точек , ( ). По методу Эйлера – Коши вычисление приближенного решения проводится следующим образом:

Вначале вычисляется первое приближение:

,

Затем находится более точное приближение:

.

Остаточный член на каждом шаге в методе Эйлера – Коши имеет порядок .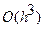

Оценка погрешности может быть получена с помощью двойного пересчета на ЭВМ. Расчет повторяют с шагом 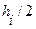и погрешность более точного решения (при шаге 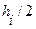) оценивают приближенно:

.

C

x1

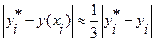Рис. 8.2. Геометрическая иллюстрация модифицированного метода Эйлера.

Расчетные формулы:

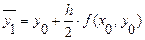- значение функции в середине отрезка [x₀, x₁].

- значение функции в конце отрезка [x₀, x₁].

Формула модифицированного метода Эйлера:

, (8.7)

где I = 0, 1, …., n-1 - номер узла;

x_i = a + i×h – координата узла;

у₀ = у(х₀) – начальное условие.

Алгоритм решения ОДУ модифицированным методом Эйлера отличается от описанного ранее алгоритма метода Эйлера, представленного на блок-схеме, только алгоритмом расчета новой точки.

Погрешность метода d » О(h³).

Усовершенствованный метод Эйлера – Коши можно еще более уточнить, применяя итерационную обработку каждого значения 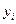. Вначале вычисляется

,

а затем это приближение уточняется по формуле:

.

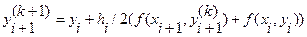Итерации продолжают до тех пор, пока в пределах требуемой точности два последовательных приближения 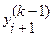и не совпадут. После чего принимается за приближенное значение .

Пример 2. Решим ранее рассмотренное уравнение (пример 1) модифицированным методом Эйлера.

Y^’ – 2×y + x² = 1, x Î [0;1], y(0) = 1.

Пусть n = 10 , h = (1 – 0)/10 = 0,1.

Начальная точка x₀ = 0, y₀ = 1.

Рассчитаем первую точку:

Аналогично рассчитаем 2, 3, … ,10 точки.

Блок-схема алгоритма расчета новой точки модифицированным методом Эйлера

Метод усредненных точек

Пусть требуется найти решение задачи Коши:

, , .

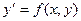Как и в методе Эйлера, на отрезке 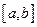зададим конечное множество точек , ( 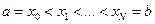). По усовершенствованному методу ломаных сначала вычисляются промежуточные значения:

, ,

а затем полагают, что

,

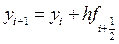где .

В этом методе для повышения точности используется усредненное значение производной на рассматриваемом отрезке:

.

В приведенной формуле y_i+1 входит в обе части уравнения и не может быть выражено явно. Чтобы обойти эту трудность, в правую часть вместо y_i+1 подставляется значение, рассчитанное по формуле Эйлера (8.5).

.

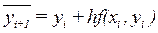Получаем формулу исправленного метода Эйлера:

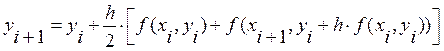, (8.8)

где I = 0, 1, …., n – 1 - номер узла;

x_i = a + i× h – координата узла;

у₀ = у(х₀) – начальное условие.

Погрешность исправленного метода Эйлера d_М = О(h³).

Алгоритм решения ОДУ методом усредненных точек отличается от описанного ранее алгоритма метода Эйлера, представленного на блок-схеме, только алгоритмом расчета новой точки.

Блок-схема алгоритма расчета новой точки средненным методом Эйлера:

Рис. 8.3. Геометрическая иллюстрация усредненного метода Эйлера.

L₁ – касательная к у(х) в начальной точке А, с tga₀ = f(x₀, y₀);

т. В – значение 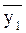вычисляется по формуле Эйлера;

L₂ – касательная к у(х) в точке В, с tga₁ = f(x₁, );

L₃ – прямая через В со среднеарифметическим углом наклона;

L₄ - прямая, параллельная L₃, проведенная через точку А.

Пример 3. Решим ранее рассмотренное уравнения (пример 1) усредненным методом Эйлера.

Y^’ – 2×y + x² = 1, x Î [0;1], y(0) = 1.

Пусть n = 10 , h = (1 – 0) / 10 = 0,1.

Начальная точка x₀ = 0, y₀ = 1.

Рассчитаем первую точку:

Аналогично можно вычислить значения функции во 2, 3, …, 10-й точках.