Графо-аналитический метод кинетостатического расчета структурных групп 2-го класса

Расчет начинают с группы, наиболее удаленной от начального звена. Исходными данными для расчета служат длины всех звеньев, массы звеньев механизма, силы «полезного» сопротивления. Инерционная нагрузка рассчитывается после проведения полного кинематического анализа механизма. Определяются силы тяжести звеньев механизма.

Последовательность кинетостатического расчета механизма заключается в следующем:

1) Механизм разбивают на группы Ассура и рассматривают равновесие каждой группы, так как добавление сил и моментов сил инерции делает статически определимой систему, действующих активных сил и возникающих реакций в этой группе;

2) Для определения реакций связей составляют уравнения равновесия плоской системы сил для всей группы Ассура или для отдельных ее звеньев в виде

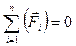, (3.5)

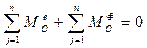, (3.6)

где 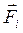– векторы сил, действующих на группу;

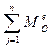– моменты внешних сил системы относительно точки О,

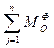–моменты внешних сил системы относительно точки О.

3) Уравнение (3.5) решают графически путем построения плана сил, уравнение (3.6) – аналитически;

4) Для определения уравновешивающей силы, которая обеспечивает заданный закон движения начального звена механизма, составляют уравнение равновесия относительно стойки О:

.

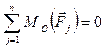5) Реакции связи стойки О находят путем построения силового многоугольника, решая уравнение (3.5).

6) Проверку правильности определения уравновешивающей силы осуществляют методом Жуковского.

Запись 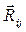понимаем как силу реакции, действующую со стороны звена «i» на звено «j», а 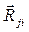принимают как реакцию, действующую со стороны звена «j» на звено «i». Из третьего закона Ньютона очевидно, что .

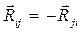При построении планов сил используют масштабный коэффициент планов сил 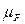, который определяется формулой:

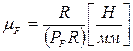, (3.7)

где 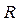– величина реакции (Н);

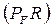– величина отрезка на плане сил, соответствующего реакции R.

Пример №6.Для заданного механизма (рис. 2.5а) определить уравновешивающую силу механизма и реакции связей, если сила «полезного» сопротивления, действующая на ползун, равна 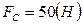. Исходные данные для кинетостатического расчета взять из примера 5.

Дано: , , , , , , , , , , .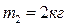

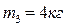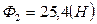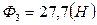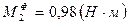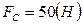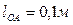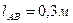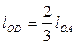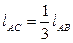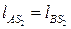Решение:

1) Определим силы тяжести звеньев механизма по формуле (3.1):

,

.

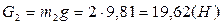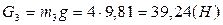Поскольку масса кривошипа 1 не задана, то весом звена 1 в расчетах пренебрегаем.

2) Проведем кинетостатический расчёт группы Ассура ВВП (АВ).

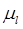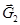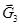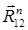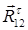Рассмотрим отдельно шатун 2 с поршнем 3, отсоединив от ведущего звена по шарниру А. Вычертим звенья 2-3 в выбранном масштабе , приложим к нему силы тяжести , ; реакции связей в точке А: и –нормальная и тангенциальная составляющие реакции 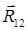(реакции, действующей со стороны звена 1 на звено 2) и в точке В: 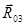–реакции, действующей со стороны стойки 0 на ползун 3; силы инерции 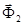, 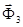и момент сил инерции 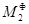, а также силу «полезного» сопротивления 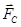на поршень 3 (см. рис. 3.5).

Рис. 3.5. Звено АВ с приложенными силами

Для определения тангенциальной составляющей реакции 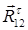составим уравнение равновесия относительно точки В по формуле (3.6):

; ,

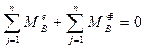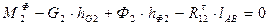где ,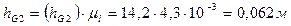

.

.

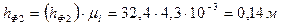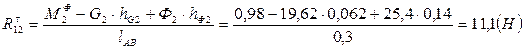Для определения остальных реакци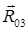й и 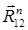построим план сил, используя уравнение (3.5):

.

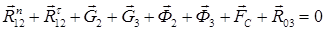Для построений выбираем масштаб плана сил по формуле (3.7):

.

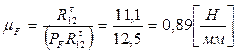Тогда величины отрезков остальных сил будут равны:

,

,

,

,

.

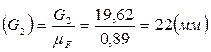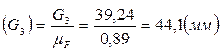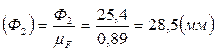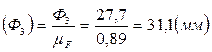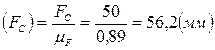Оставшиеся реакци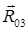и и 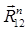определятся из построений. Строим план сил (рис. 3.6).

a) В произвольном месте чертежа ставим точку 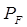– полюс плана сил.

b) Через полюс 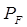проводим линию, параллельную вектору 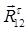, и в сторону направления вектора откладываем отрезок .

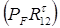c) С другой стороны, через полюс 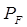проводим линию действия вектора 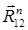– параллельно данному вектору (направление пока еще не известно).

d) Из конца вектора 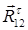проводим линию, параллельную вектору 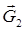, и в сторону направления вектора откладываем отрезок 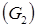и т.д.

e) Из конца последнего вектора 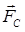проводим линию действия силы 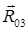до пересечения с линией действия .

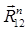f) Силовой многоугольник замкнулся. Определяем направление векторов 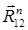, 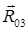и их численное значение по формулам:

,

.

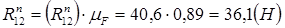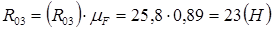Для дальнейшего кинетостатического исследования нам понадобится значение полной реакции 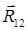, которую определим по формуле:

.

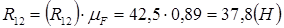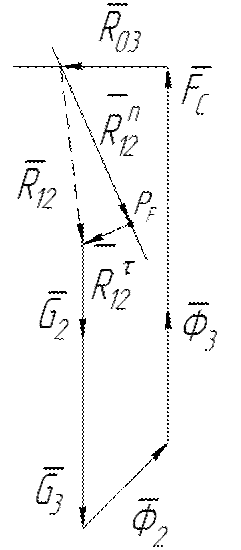
Рис. 3.6. План сил для звена АВ

3) Проведем кинетостатический расчёт кривошипа АО.

Рассмотрим кривошип 1 отдельно, отсоединив его от остального механизма по шарниру А. Вычертим звено 1 в выбранном масштабе 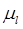, приложим к нему реакцию связи в точке А: 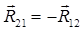(реакцию, действующую со стороны звена 2 на звено 1) и в точке О: 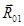– реакцию, действующей со стороны стойки 0 на кривошип1. Поскольку направление реакции 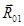заранее не известно, то заменим ее составляющими по осям х и y ( 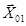и 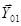соответственно). В точке А прикладываем уравновешивающую силу, направленную перпендикулярно кривошипу (см. рис. 3.7).

Рис. 3.7. Ведущее звено с приложенными силами

Для определения уравновешивающей силы 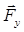составим уравнение равновесия относительно точки О по формуле (3.6):

; ,

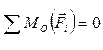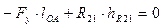где ,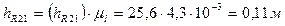

.

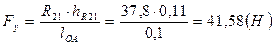Для определения остальных реакци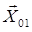й и 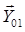построим план сил, используя уравнение (3.5):

.

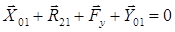Для построений выбираем масштаб плана сил по формуле (3.7):

.

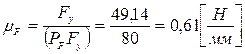Тогда величина отрезка 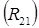будет равна:

.

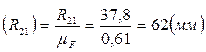Оставшиеся реакци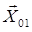и и 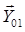определятся из плана сил, поскольку линии действия этих реакций известны, а направление определиться построением. Строим план сил (рис. 3.8).

Определяем численное значение полной реакции 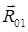по формуле:

.

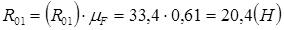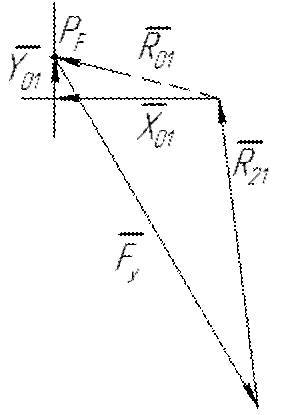
Рис. 3.8. План сил ведущего звена