Стандартизированное уравнение

Линейной множественной регрессии

Если коэффициенты линейной множественной регрессии рассматривать в качестве показателей влияния факторов, то следует иметь в виду, что коэффициенты регрессии в уравнении

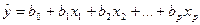(3.7)

между собой прямо не сравнимы. Их численные значения зависят от выбранных единиц измерения каждого фактора.

Чтобы коэффициенты регрессии стали сравнимы, приведем коэффициенты регрессии к стандартизированному масштабу.

Для этого все переменные выражаются в безразмерных, так называемых стандартизированных, единицах измерения при помощи соотношений:

,

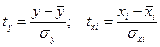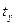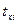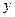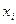где и – соответствующие значения факторов и в стандартизированном масштабе. Свободный элемент 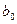в стандартизированном уравнении отсутствует, т.е. уравнение (3.7) можно записать в виде:

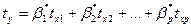(3.8)

Коэффициенты 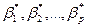называются коэффициентами регрессии в стандартизированном масштабе. Переход от коэффициентов 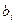к 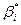и обратно можно осуществить по формулам:

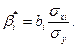
Коэффициенты регрессии (3.8) показывают влияние изменения каждой переменной на изменение фактора 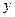. Все коэффициенты выражены в сравнимых единицах измерения. Чем больше 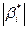, тем сильнее влияет соответствующий факторный показатель на результативный.

Контрольные вопросы:

1. Как определяется модель множественной линейной регрессии?

2. Перечислите предпосылки МНК. Каковы последствия их невыполнимости?

3. Что характеризуют коэффициенты регрессии?

4. В чем суть МНК для построения множественного линейного уравнения регрессии?

5. Опишите алгоритм определения коэффициентов множественной линейной регрессии по МНК в матричной форме.

6. Как записывается решение с помощью МНК в матричной форме?

7. Как определяется стандартизированное уравнение линейной множественной регрессии?

8. Чем отличаются уравнения множественной регрессии в натуральном и стандартизованном масштабе?

9. Каковы свойства стандартизованных переменных?

10. Как оценить значимость модели регрессии в целом?

ТЕМА 4. МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ

План лекции

1. Множественная линейная корреляционная зависимость.

2. Частные коэффициенты корреляции.

3. Коэффициенты множественной корреляции.

4. Отбор факторов в случае линейной множественной регрессии

Введение

Особенностью множественной регрессии и корреляции является необходимость различать случаи корреляционной множественной связи, когда переменные 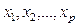являются случайные величинами; регрессионной, если переменные 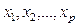– неслучайными величинами, а также смешанный случай, когда некоторые из переменных – случайные величины, а другие – неслучайные.

Отбор факторов 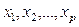, существенно влияющих на фактор 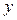при наличии возможностей внутренней взаимосвязи между переменными 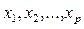осуществляется обычно в несколько этапов. Сначала отбираются факторы, связанные с изучаемым явлением на основе данных теоретического исследования (экономическая теория, заключения специалиста и т.д.). При этом для построения множественной регрессии и корреляции отбираются факторы, которые могут быть количественно измеримы.

Далее отобранные факторы подвергаются проверке существенности их влияния на изучаемый показатель с использованием методов математической статистики. Такая проверка, как правило, включает анализ матрицы парных коэффициентов корреляции, частных корреляций, проверку существенности (значимости) коэффициентов регрессии на основе 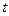–критерия, анализ остатков (отклонений) и т.д.