Построение интервальных прогнозов

По модели парной регрессии

В прогнозных расчетах по уравнению регрессии определяется предсказуемое 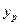значение как точечный прогноз 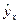при подстановки в линейное уравнение регрессии 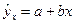соответствующего значения 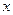. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки 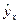, т.е. 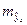, и соответственно мы получаем интервальную оценку прогнозного значения :

.

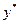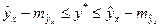Для того чтобы понять, как строится формула для определения величин стандартной ошибки 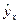, подставим в уравнение линейной регрессии выражение параметра :

,

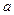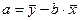тогда уравнение регрессии примет вид:

.

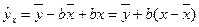Отсюда следует, что стандартная ошибка 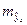зависит от ошибки 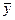и ошибки коэффициента регрессии 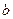, т.е.

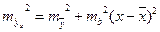. (2.27)

Считая, что прогнозное значение фактора 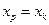, получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения, т.е. :

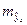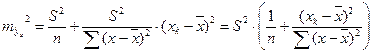. (2.28)

Соответственно 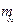имеет выражение:

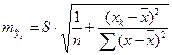. (2.29)

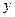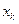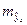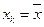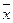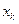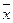Рассмотренная формула стандартной ошибки предсказываемого среднего значения при заданном значении характеризует ошибку положения линии регрессию. Величина стандартной ошибки достигает минимума при и возрастает по мере того, как «удаляется» от в любом направлении. Иными словами, чем больше разность между и , тем больше ошибка 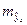, с которой предсказывается среднее значение 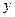для заданного значения .

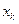Для примера 2.1 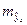составит:

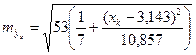
При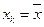

.

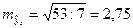При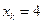

.

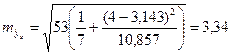Соответственно 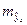составит эту же величину и при 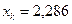. Для прогнозируемого значения 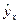95%-ные доверительные интервалы при заданном 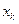определяется выражением

,

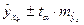т.е. 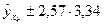или .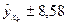

При 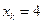прогнозное значение 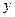составит:

,

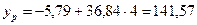которое представляет собой точечный прогноз.

Прогноз линии регрессии в интервале составит:

.

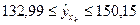Контрольные вопросы:

1. Что такое функция регрессии?

2. Назовите основные причины наличия в регрессионной модели случайного отклонения.

3. Какой вид имеет линейная парная регрессионная модель?

4. Каковы основные предпосылки регрессионного анализа?

5. В чем заключается теорема Гаусса-Маркова?

6. В чем суть метода наименьших квадратов?

7. Какие выводы можно сделать об оценках коэффициентов регрессии и случайного отклонения, полученных по МНК?

8. Какова концепция F-критерия Фишера?

9. Что выражает коэффициент корреляции?

10. Каковы основные свойства коэффициента корреляции?

11. Как определяют коэффициент детерминации? Что он показывает?

ТЕМА 3. МНОЖЕСТВЕННЫЙ

РЕГРЕССИОННЫЙ АНАЛИЗ

План лекции

1. Классическая нормальная линейная модель множественной регрессии.

2. Оценка параметров классической регрессионной модели методом наименьших квадратов.

3. Предпосылки для множественного регрессионного анализа.

4. Стандартизированное уравнение линейной множественной регрессии.

Введение

Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. Возникает задача исследования зависимости одной зависимой переменной 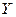от нескольких объясняющих переменных: Х₁, Х₂, …, Х_Р. Эта задача решается с помощью множественного регрессионного анализа.

Множественная регрессия представляет собой регрессию результативного признака с двумя или большим числом независимых переменных вида

.

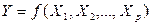В уравнении регрессии случайная величина 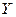зависит не только от значений независимых переменных 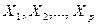, но и от ряда других факторов, влияющих на 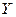, которые не могут быть проконтролированы. В связи с этим будем использовать запись вида

,

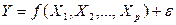где 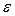- случайная величина, характеризующая отклонение результативного признака от теоретического, найденного по уравнению регрессии.

Статистический анализ случайной ошибки является одной из основных задач эконометрики.

При исследовании зависимости результативного признака 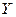от ряда факторов 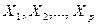необходимо решать такие же задачи, что и при парной связи двух переменных 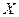и :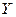

· определение вида регрессии;

· оценка параметров;

· определение тесноты связи, если переменные 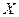и 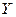- случайные величины.

Однако наряду с этими задачами необходимо рассматривать и ряд задач, характерных лишь для множественной регрессии и корреляции. К таким задачам относится отбор факторов 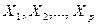, существенно влияющих на фактор 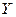, при наличии возможностей внутренней взаимосвязи между переменными 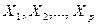. Такой отбор требует прежде всего глубокого теоретического и практического знания качественной стороны рассматриваемых экономических явлений.